LeetCode刷题——分支限界法(C/C++)
目录
- [简单]101. 对称二叉树
- [简单]102. 二叉树的层序遍历
- [简单]111. 二叉树的最小深度
- [简单]110. 平衡二叉树
- [中等]200. 岛屿数量
分支限界法与回溯法的不同
(1)求解目标:回溯法的求解目标是找出解空间树中满足约束条件的所有解,而分支限界法的求解目标则是找出满足约束条件的一个解,或是在满足约束条件的解中找出在某种意义下的最优解。
(2)搜索方式的不同:回溯法以深度优先的方式搜索解空间树,而分支限界法则以广度优先或以最小耗费优先的方式搜索解空间树。
[简单]101. 对称二叉树
- 原题链接
- 题解
比较基础的递归思想,按照对称点的方式递归,递归函数中,第一个参数是左半边的点,第二个参数是右半边的对称点,因此,进入子节点递归的时候,左半边的点进入其左孩子时,右半边的对称点要进入其右孩子,左半边的点进入其右孩子时,右半边的对称点要进入其左孩子。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if(root == nullptr) return true;
return recursion(root->left,root->right);
}
bool recursion(TreeNode* left, TreeNode* right){
if(left == nullptr && right == nullptr) return true;
else if(left == nullptr || right == nullptr) return false;
if(left->val != right->val) return false;
if(!recursion(left->left,right->right)) return false;
if(!recursion(left->right,right->left)) return false;
return true;
}
};
[简单]102. 二叉树的层序遍历
- 原题链接
- 题解
经典的借助队列进行层序遍历的思路,在while循环中再加一层for循环,来区别每一层的节点即可
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> q;
vector<vector<int>> ans;
vector<int> nums;
if(root == nullptr) return ans;
q.push(root);
while(!q.empty()){
int n = q.size();
nums.clear();
for(int i=0;i<n;i++){
TreeNode* node = q.front();
q.pop();
nums.push_back(node->val);
if(node->left) q.push(node->left);
if(node->right) q.push(node->right);
}
ans.push_back(nums);
}
return ans;
}
};
[简单]111. 二叉树的最小深度
- 原题链接
- 题解
层序遍历,一旦有哪一层节点是叶子节点,直接return即可
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//广度优先遍历,一旦找到叶子节点,返回深度并停止遍历
int minDepth(TreeNode* root) {
if(root == nullptr) return 0;
queue<TreeNode*> q;
q.push(root);
int deep = 0;
while(!q.empty()){
int n = q.size();
deep++;
for(int i=0;i<n;i++){
TreeNode* node = q.front();
q.pop();
if(node->left) q.push(node->left);
if(node->right) q.push(node->right);
if(node->left == nullptr && node->right == nullptr){
return deep;
}
}
}
return deep;
}
};
[简单]110. 平衡二叉树
- 原题链接
- 题解
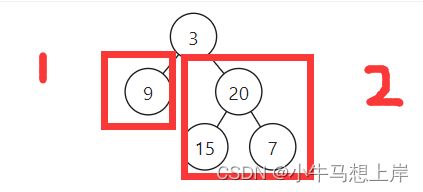
每次递归先获取左右子树的高度,分别为leftDepth与rightDepth,二者的差值可在[-1,0,1]中则表示以当前节点为根的子树是平衡的,如果不平衡就返回-1,一旦收到左右子树有返回-1,则当前节点也直接返回-1,保证将不有序的情况层层向上传递。
ps:(这题其实还简化了,在数构里面一半平衡树是基于有序树的基础上保证平衡,这种情况需要多判断一下各个节点是否满足有序树)。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isBalanced(TreeNode* root) {
if(root == nullptr) return true;
if(dfs(root) < 0) return false;
return true;
}
int dfs(TreeNode* p){
if(p == nullptr) return 0;
if(!p->left && !p->right){
return 1;
}
int leftDepth = 0;
int rightDepth = 0;
if(p->left) {
leftDepth = dfs(p->left);
if(leftDepth < 0) return -1;
}
if(p->right) {
rightDepth = dfs(p->right);
if(rightDepth < 0) return -1;
}
int diff = leftDepth-rightDepth;
if(diff >= -1 && diff <= 1){
return max(leftDepth,rightDepth) + 1;
}
return -1;
}
};
[中等]200. 岛屿数量
- 原题链接
- 题解
比较基础的多次深度优先遍历的题,对一个值为1的点,进入递归将其所有通过上下左右可到达的1标记为0,可以形象为用海水覆盖,这样下次就不会再遍历到,整个岛屿被覆盖后,就回到循环去找下一个岛屿。
class Solution {
public:
int numIslands(vector<vector<char>>& grid) {
int count = 0;
for(int i=0;i<grid.size();i++){
for(int j=0;j<grid[i].size();j++){
if(grid[i][j] == '1'){
count++;
dfs(grid,i,j);
}
}
}
return count;
}
void dfs(vector<vector<char>>& grid,int i,int j){
cout << i << " " << j << endl;
grid[i][j] = '0';//先覆盖当前点,之后便不会再扫描到他
//向左检查
if(j>0 && grid[i][j-1] == '1') dfs(grid,i,j-1);
//向右检查
if(j<grid[i].size()-1 && grid[i][j+1] == '1') dfs(grid,i,j+1);
//向上检查
if(i>0 && grid[i-1][j] == '1') dfs(grid,i-1,j);
//向下检查
if(i<grid.size()-1 && grid[i+1][j] == '1') dfs(grid,i+1,j);
}
};