图像去噪（包含修正的阿尔法均值滤波及通用滤波方法代码）

原理

• 高斯噪声
  高斯噪声是指它的概率密度函数服从高斯分布（即正态分布）的一类噪声。如果一个噪声，它的幅度分布服从高斯分布，而它的功率谱密度又是均匀分布的，则称它为高斯白噪声。高斯白噪声的二阶矩不相关，一阶矩为常数，是指先后信号在时间上的相关性。高斯白噪声包括热噪声和散粒噪声。在通信信道测试和建模中，高斯噪声被用作加性白噪声以产生加性白高斯噪声。
• 椒盐噪声
  椒盐噪声也称为脉冲噪声，是图像中经常见到的一种噪声，它是一种随机出现的白点或者黑点，可能是亮的区域有黑色像素或是在暗的区域有白色像素（或是两者皆有）。盐和胡椒噪声的成因可能是影像讯号受到突如其来的强烈干扰而产生、类比数位转换器或位元传输错误等。例如失效的感应器导致像素值为最小值，饱和的感应器导致像素值为最大值。
• 中值滤波
  对待处理的当前像素，选择一个模板3x3、5x5或其他，这里选择3x3矩阵，该模板为其邻近的若干个像素组成，对模板的像素由小到大进行排序，再用模板的中值来替代原像素的值的方法。
• 修正的阿尔法均值滤波
  统计排序滤波器的响应基于由该滤波器包围的图像区域中的像素值的排序，为一种非线性滤波器。常用的非线性滤波器有中值滤波器、、自适应中值滤波、最大值（最小值）滤波器、中点滤波器与修正的阿尔法均值滤波器等。
  修正的阿尔法均值滤波器类似于去掉最高分与去掉最低分评价一个选手水平的方法，即将滤波范围内的数据进行排序，从大到小的顺序去除d个数据，从小到大的顺序去除d个数据，将剩下的数据计算均值。这样的滤波器，很擅长去除椒盐噪声与其他类型噪声一起污染过的图片。

实际操作（先加噪声再去噪）

1. 加噪声
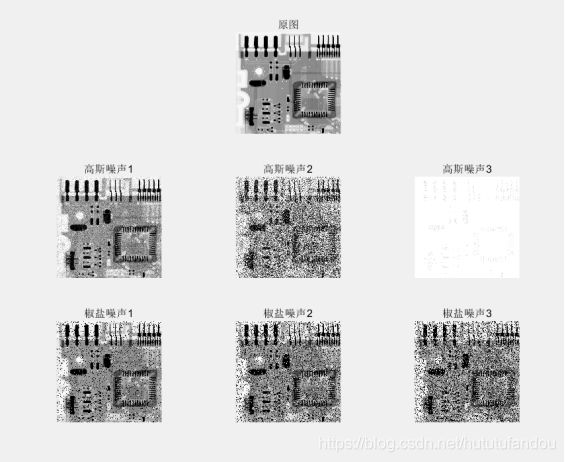
   如图所示，为不同噪声强度的加噪声处理。对高斯噪声，改变高斯函数的均值和方差即可产生不同强度噪声。对椒盐噪声，在代码实现中，对于某一个特定位置产生两个随机数，设定一个阈值，若大于阈值则置1，小于阈值则置0，再通过对两个随机数进行逻辑运算（交并补），可实现在对应位置加椒盐噪声。改变阈值即可实现不同噪声强度的加噪声处理。
   
2. 不同滤波方法去噪
   
3. 不同滤波器原理分析与比较

• 算数均值滤波
  算术均值滤波即滤波后的中心点像素值为原图中中心点范围内的像素值的平均值。
  对本张经过椒盐噪声和高斯噪声处理的图片，算术均值滤波的结果并不十分理想，因为椒盐噪声的像素值为0或255，经过算数均值滤波处理后，模糊了图片原本的信息，会使图片处于“灰蒙蒙”的状态。
• 几何均值滤波
  几何均值滤波即滤波后的中心点像素值为原图中中心点范围内的像素值的乘积开根号，开根号的次数为滤波器长宽乘积的倒数。
  对本张经过椒盐噪声和高斯噪声处理的图片，几何均值滤波的处理结果十分不理想，由几何均值滤波的公式可知，若滤波器范围内有一个像素值为0，则处理后的中心像素点的值均为0，这是由公式中的连乘性质决定的。而由于原图像经过椒盐处理，有很多像素值为“椒”噪声，即为0。由此可知，处理后的图像中有很多像素均为0，展示出来的是黑色像素。
• 中值滤波
  中值滤波原理如以上2.3所述，在本实验中，中值滤波可以很好的处理椒盐噪声，因为一个区域内的像素值的中值不太可能是255或0，因此很好的处理了椒盐噪声。而对于高斯噪声的处理，本滤波器就没有什么独到之处了。
• 修正阿尔法均值滤波
  修正阿尔法均值滤波原理如以上2.4所述，在本实验中，修正的阿尔法均值滤波的表现差强人意，由其原理，它最大程度上去除了椒盐噪声，并模糊了原图像。
• 不同滤波器的比较分析
  在本实验中，中值滤波的表现可以说是最为良好的。不同滤波器的优势和劣势均如上所述，

1. 几何均值滤波会让滤波后的图像过多“黑”像素。
2. 由于椒盐噪声存在，算数均值滤波表现不良好，会让滤波后的图像处于“灰蒙蒙”的状态
3. 修正的阿尔法均值滤波去除了“极端像素点”，再进行平均滤波，效果就要比算术均值滤波好很多了。

源代码

picture=imread('ckt-board-orig.tif');
[m,n]=size(picture);

y1=0+0.1*randn(m,n);%二维高斯分布矩阵 0是均值 0.1是标准差
%先将其double化，再除以255 便于后面计算
gauss1=double(picture)/255;
%加上噪声
gauss1=gauss1+y1;
%将像素范围扩大至0--255
gauss1=gauss1*255;
%转换为uint8类型
gauss1=uint8(gauss1);

y2=0+0.4*randn(m,n);
gauss2=double(picture)/255;
gauss2=gauss2+y2;
gauss2=gauss2*255;
gauss2=uint8(gauss2);

y3=1+0.1*randn(m,n);
gauss3=double(picture)/255;
gauss3=gauss3+y3;
gauss3=gauss3*255;
gauss3=uint8(gauss3);

salt1=picture;
k1=0.1;
k2=0.1;
a1=rand(m,n)<k1;
a2=rand(m,n)<k2;
salt1(a1&a2)=255;
salt1(a1& ~a2)=0;

salt2=picture;
k1=0.2;
k2=0.2;
a1=rand(m,n)<k1;
a2=rand(m,n)<k2;
salt2(a1&a2)=255;
salt2(a1& ~a2)=0;

salt3=picture;
k1=0.3;
k2=0.3;
a1=rand(m,n)<k1;
a2=rand(m,n)<k2;
salt3(a1&a2)=255;
salt3(a1& ~a2)=0;


figure(1);
subplot(3,3,2),imshow(picture),title('原图');
subplot(3,3,4),imshow(gauss1),title('高斯噪声1');
subplot(3,3,5),imshow(gauss2),title('高斯噪声2');
subplot(3,3,6),imshow(gauss3),title('高斯噪声3');
subplot(3,3,7),imshow(salt1),title('椒盐噪声1');
subplot(3,3,8),imshow(salt2),title('椒盐噪声2');
subplot(3,3,9),imshow(salt3),title('椒盐噪声3');

GSalt=gauss1;
k1=0.1;
k2=0.1;
a1=rand(m,n)<k1;
a2=rand(m,n)<k2;
GSalt(a1&a2)=255;
GSalt(a1& ~a2)=0;

%算术均值
dGSalt=im2double(GSalt);
resultImage1=dGSalt;
for i=2:m-1
    for j=2:n-1
        resultImage1(i,j)=(dGSalt(i-1,j-1)+dGSalt(i-1,j)+dGSalt(i-1,j+1)+dGSalt(i,j-1)+dGSalt(i,j)+dGSalt(i,j+1)+dGSalt(i+1,j-1)+dGSalt(i+1,j)+dGSalt(i+1,j+1))/9;
    end
end
resultImage1=im2uint8(resultImage1);

resultImage2=dGSalt;
for i=2:m-1
    for j=2:n-1
        resultImage2(i,j)=(dGSalt(i-1,j-1)*dGSalt(i-1,j)*dGSalt(i-1,j+1)*dGSalt(i,j-1)*dGSalt(i,j)*dGSalt(i,j+1)*dGSalt(i+1,j-1)*dGSalt(i+1,j)*dGSalt(i+1,j+1))^(1/9);
    end
end
%resultImage=resultImage2;
resultImage2=im2uint8(resultImage2);

for r=2:m-1
    for c=2:n-1
       median3x3 =[GSalt(r-1,c-1)    GSalt(r-1,c)    GSalt(r-1,c+1)
                   GSalt(r,c-1)      GSalt(r,c)      GSalt(r,c+1)
                   GSalt(r+1,c-1)   GSalt(r+1,c)    GSalt(r+1,c+1)];
       sort1=sort(median3x3,2,'descend');
       sort2=sort([sort1(1),sort1(4),sort1(7)],'descend');
       sort3=sort([sort1(2),sort1(5),sort1(8)],'descend');
       sort4=sort([sort1(3),sort1(6),sort1(9)],'descend');
       mid_num=sort([sort2(3),sort3(2),sort4(1)],'descend');
       Median_Img(r,c) = mid_num(2);
    end
end

a=5; 
b=5;
alpha=dGSalt;
for i=1:m-a+1
    for j=1:n-a+1
        g3=dGSalt(i:i+a-1,j:j+a-1);
        g3=sort(g3(:)); %对邻域内的像素点进行排序
        min_num=ceil(b/2); %去掉最小灰度值的个数
        max_num=floor(b/2); %去掉最大灰度值的个数
        %去掉d个最值灰度级后求算术均值
        g3(1:min_num)=zeros(min_num,1);
        g3(a*a-max_num+1:a*a)=zeros(max_num,1);
        s3=sum(g3);
        %中心点的值用子图像的算术均值代替
        alpha(i+(a-1)/2,j+(a-1)/2)=s3/(a*a-b); 
    end
end



figure(2);
subplot(2,3,1),imshow(picture),title('原图');
subplot(2,3,2),imshow(GSalt),title('高斯+椒盐');
subplot(2,3,3),imshow(resultImage1),title('算术均值滤波');
subplot(2,3,4),imshow(resultImage2),title('几何均值滤波');
subplot(2,3,5),imshow(Median_Img),title('中值滤波');
subplot(2,3,6),imshow(alpha),title('修正阿尔法均值滤波');