数据分析——A/B测试及其实战

1. 什么是A/B测试

A/B测试是为 web 或 app 界面或流程制作两个（A/B）或多个版本，在同一时间维度，分别让组成成分相同（相似）的访客群组（目标人群）随机的访问这些版本，收集各群组的用户体验数据和业务数据，最后分析、评估出最好版本，正式采用。

2. A/B测试目的

1. 消除客户体验（UX）设计中不同意见的纷争，根据实际效果确定最佳方案；

2. 通过对比试验，找到问题的真正原因，提高产品设计和运营水平；

3. 建立数据驱动、持续不断优化的闭环过程；

4. 通过A/B测试，降低新产品或新特性的发布风险，为产品创新提供保障。

3. A/B测试基本步骤

1. 分析现状并建立假设：分析业务数据，确定当前最关键的改进点，并作出优化的假设。提出优化的建议。

2. 设定目标，制定方案：设置主要目标，用来衡量各优化版本的优劣；设置辅助目标，用来评估优化版本对其他方面的影响。

3. 设计与开发：制作2个或多个优化版本的设计原型并完成技术实现。

4. 分配流量：确定每个线上测试版本的分流比例，初始阶段，优化方案的流量设置可以较小，根据情况逐渐增加流量。
   

5. 采集并分析数据：收集实验数据，进行有效性和效果判断：统计显著性达到95%或以上并且维持一段时间，实验可以结束；如果在95%以下，则可能需要延长测试时间；如果很长时间统计显著性不能达到95%甚至90%，则需要决定是否中止试验。

6. 做出决策：根据试验结果确定发布新版本、调整分流比例继续测试或者在试验效果未达成的情况下继续优化迭代方案重新开发上线试验。

北极星指标（North Star Metric），也叫作第一关键指标（One Metric That Matters），是指在产品的当前阶段与业务/战略相关的绝对核心指标，一旦确立就像北极星一样闪耀在空中，指引团队向同一个方向迈进。

4. A/B测试的原理——假设检验

因为AB测试是检验来自两个组样本平均数的差异性，从而判断它们各自代表的总体的差异是否显著，因此使用的是两个总体均值之差的检验。即使用统计量Z。具体见假设检验假设检验。

5.A/B测试的关键点

目标KPI

A/B测试中我们需要制定目标KPI：指评判AB测试效果优劣的最终指标。例如：提升多少点击率或者提升多少转化率。

策略

为了达到我们制定的目标KPI，我们需要采取一定的策略：AB组分别采取的策略的差异点。例如：改变商品展示图片，改变文案等等；一般有多少个差异点就需要多少次测试；

A/B测试的作用

• 目标KPI的最大化：找到对KPI最优的策略，保证目标KPI最大化；
• 后续分析，沉淀诀窍：由于人群中有差异，通过研究不同子人群对于不同策略的响应程度，可以获得每组人群在策略上的偏好，帮助未来更好的个性化创新和设计。

6. AB测试常见问题和应对方案

1. 如何分配流量

• 零售行业的线下AB测试，一般用于测试不同优惠券带来的业务指标的变化。基于优惠券的具体设置方式，对流量分配有着不同的实施方法。
  • 多种优惠券设计相似：流量均分，4组策略每组20%，对照组20%
  • 优惠券设计不确定性大：最小化测试组，10%测试，90%对照
  • 优惠券效用过，仅为追踪效果：少量对照组，10%对照，90%测试
• 常用的分流方法
  • sql中的rand函数
  • 利用尾数的随机ID

不管如何做分流，用来做对照组和测试组的用户要做好标记方便之后进行分析和统计。

2.如何确定测试的最小人数

随机波动：由于我们的测试样本不可能都一模一样，所以我们设定的两个一模一样的对照组的结果也有可能出现不一样的结果，这就是随机波动。随机波动会进一步影响测试的结果。
最小样本量：为了使测试结果显著有效的同时保证最小的成本，我们首先要确保测试组里人数最少的一组达到验证效果有效性的最小样本数量。现在我们有很多网站可以帮我们计算最小样本量，网站如下A/B测试样本量计算网站

• 比例类目标KPI：
  

• baseline conversion rate：基准率，例如：点击率；
• minimum detectable effect：最小特侧率，例如：提升3%的点击率；
• significance level α：显著水平，一般为5%；
• statistical power 1-β：统计功效也就是$H_0$错误并拒绝$H_0$，一般取80%或者90%，这里需要理解弃真错误和取假错误

	$H_0$是对的	$H_0$是错的
接受$H_0$	(1-α)这没问题	β 取假错误
拒绝$H_0$	α 弃真错误	(1-β)这也没问题

这里的α弃真错误也叫第一类错误，β取假错误也叫第二类错误。

• 均值类目标KPI：
  
  如果测试过程中比例和均值两个指标都要对比，则选择数值大的那个。

3. 如何避免辛普森悖论

辛普森悖论：在某个条件下的两组数据，分别讨论时都会满足某种性质，可是一旦合并考虑，却可能导致相反的结论。

导致辛普森悖论的原因：

流量分割不均匀导致的实验组与对照组的用户特征不一致。

如何避免辛普森悖论：

• 合理的进行正确的流量分割，保证试验组和对照组里的用户特征是一致的，并且都具有代表性，可以代表总体用户特征。
• 试验设计：两个变量对试验结果都有影响，就应该把这两个变量放在同一层进行互斥试验，不要让一个变量的试验动态影响另一个变量的检验。

例如：我们觉得一个试验可能会对新老客户产生完全不同的影响，那么就应该对新客户和老客户分别展开定向试验，观察结论。

• 试验实施：要积极的进行多维度的细分分析，除了总体对比，也看一看对细分受众群体的试验结果，不要以偏盖全，也不要以全盖偏。

例如：一个试验版本提升了总体活跃度，但是可能降低了年轻用户的活跃度，那么这个试验版本是不是更好呢？一个试验版本提升总营收0.1%，似乎不起眼，但是可能上海地区的年轻女性 iPhone 用户的购买率提升了20%，这个试验经验就很有价值了。

7. A/B测试案例

项目背景

公司给网站投放广告的时候，一开始给用户看到的落地页是访问课程资料,现在公司又推出了开始免费试学这个落地页。

• 目前的转化率全年平均在13%左右
• 目标转化率达到15%。

a) 提出假设

$H_0$原假设：旧版的落地页好，新版的不好用
$H_1$备择假设：新的落地页好

b) 制定方案

选择变量

• 对照组：看到旧的页面
• 实验组：看到新的页面

虽然我们已经知道了旧的设计的转化率(13%左右), 但是我们依然要需要设计两组, 原因是为了避免其他因素带来的误差, 比如季节因素, 促销因素。这两组人在其它条件都相同的只是页面设计不同的情况下进行实验， 这样能保证两组间的差异是由于设计导致的。

确定目标KPI

转化率由13%提高到15%，为此我们记录用户是否转化的标识。

确定试验人数

虽然人数越多结果越准确，我们需要用到最小的成本来完成A/B测试，并保证结果的有效性，所以进行试验人数计算。

• 可以通过上面的网站计算人数为4523人次。
  
• 通过python计算人次4720。

import pandas as pd
import statsmodels.stats.api as sms

# 计算effect size
effect_size = sms.proportion_effectsize(0.13,0.15)
requried_num = sms.NormalIndPower().solve_power(effect_size, power=0.8, alpha=0.05, ratio=1)
print('测试最小人数为：',requried_num)

我们这里取4523。

c) 分配流量

通过对userid进行hash，将用户分成两组old_page和new_page

d) 采集数据

准备和收集数据需要跟工程师团队配合，这里我们根据已有的数据每组采集出4523条数据。

# 导入包和数据
import pandas as pd
user_df = pd.read_csv('ab_data.csv', sep=',', encoding='utf-8')
user_df.head()

user_df.info()

删除重复用户。

session_count = user_df.user_id.value_counts()
multi_user = session_count[session_count>1].count()
print('重复的用户数量：',multi_user)
drop_user = session_count[session_count>1].index
user_df_no_multi = user_df[-user_df['user_id'].isin(drop_user)]
print('删除重复后的用户数量：',user_df_no_multi.shape[0])

user_df_no_multi.pivot_table(index='group', columns='landing_page', values='user_id', aggfunc='count')

我们能够发现，测试组合对照组的网页对应是一样的。

• 采集试验组和对照组的数据

required_n = 4523
control_sample = user_df_no_multi[user_df_no_multi['group'] == 'control'].sample(n = required_n, random_state=22)
treatment_sample = user_df_no_multi[user_df_no_multi['group'] == 'treatment'].sample(n = required_n, random_state=22)
ab_test = pd.concat([control_sample, treatment_sample], axis=0)
ab_test.reset_index(drop=True, inplace=True)
ab_test.shape[0]

查看数据情况

ab_test.groupby('landing_page')['group'].value_counts()

e) 分析数据

计算两组的转化率和标准差

import numpy as np
conversion_rate = ab_test.groupby('group')['converted']
std = lambda x: np.std(x, ddof=0)
conversion_rate = conversion_rate.agg([np.mean, std])
conversion_rate.columns = ['conversion_rate', 'std']
conversion_rate

从上表可以看出两组的转化率很接近，如下图所示：

import matplotlib.pyplot as plt
import matplotlib
import seaborn as sns
%matplotlib inline
plt.figure(figsize=(8,6))
sns.barplot(x=ab_test['group'], y=ab_test['converted'], ci=False)
plt.ylim(0, 0.17)
plt.title('Conversion rate by group', pad=20)
plt.xlabel('Group', labelpad=15)
plt.ylabel('Converted (proportion)', labelpad=15)

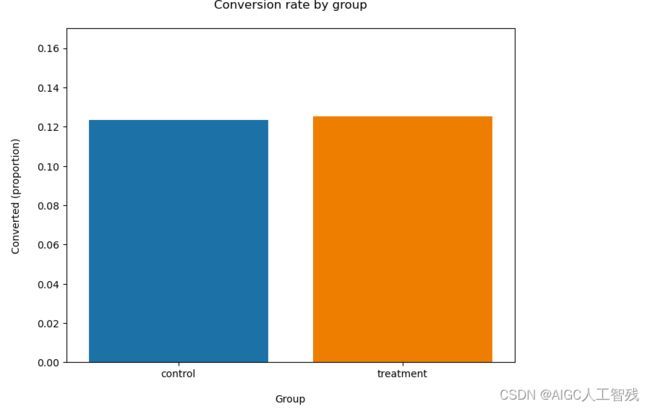
我们的试验组比测试组的数据要好一些，但是否能够说明我们的试验组达到了我们的目标呢？这就需要我们用到假设检验。

假设检验

由于两种落地页的用户数据都大于30，所以选择z统计量

• 使用statsmodels.stats.weightstats完成z检验

import statsmodels.stats.weightstats as sw
control_result = ab_test.query("group=='control'").converted
treatment_result = ab_test.query("group=='treatment'").converted
z,pval = sw.ztest(control_result,treatment_result)
print(z,pval)

from statsmodels.stats.proportion import proportions_ztest, proportion_confint
n_con = control_result.count()
n_treat = treatment_result.count()
successes = [control_result.sum(), treatment_result.sum()]
nobs = [n_con, n_treat]
z_stat, pval = proportions_ztest(successes, nobs=nobs)
(lower_con, lower_treat), (upper_con, upper_treat) = proportion_confint(successes, nobs=nobs, alpha=0.05)
print(f'z statistic: {z_stat:.2f}')
print(f'p-value: {pval:.3f}')
print(f'ci 95% for control group: [{lower_con:.3f}, {upper_con:.3f}]')
print(f'ci 95% for treatment group: [{lower_treat:.3f}, {upper_treat:.3f}]')

结论

• p-value = 0.9050582054934148>0.05，所以不能拒绝原假设，即旧落地页更好，则我们的新落地页并不能带来更好的转化。
• 置信区间可以看到我们的对照组转化率在正常水平内，而试验组转化率不在正常水平内。这意味着我们对照组和试验组的转化率很接近，我们的新落地页并没有改进作用。