单调栈和单调队列及其相关应用

        前言：好久没更新了，痛苦的期末考试周终于过去了，我可以回来继续更新了，今天我们就来学习单调栈和单调队列的相关知识及其应用，单调栈和单调队列是在算法中常用的两种数据结构，用于解决一些与区间最值相关的问题。它们的主要区别在于操作的顺序不同，单调栈是一种后进先出的数据结构，而单调队列是一种先进先出的数据结构。

目录

1.单调栈

1.1单调栈的例题引入

1.2 单调栈-下标作为栈元素

1.3总体区间最值问题 

1.4部分区间最值问题

2.单调队列 

2.1 单调队列的例题引入

2.2区间最值问题

3.金句频道

---

1.单调栈

       单调栈是一个栈，它在任何时候都保持单调递增或单调递减。通俗的说，就是从栈底到栈顶的元素可以形成一个单调不降或单调不增的序列。

使用单调栈的主要场景是求解区间最值问题，例如：

• 求解数组中所有元素的下一个或上一个更大元素，下一个或上一个更小元素。
• 求解某一区间内最大值或最小值。

使用单调栈可以在O(n)时间内解决上述问题，而使用普通的算法可能需要O(n^2)的时间复杂度。

1.1单调栈的例题引入

       首先，暴力解法是行不通的，因为我们有10^5个数据，每次都从i-1 -> 0进行遍历查找的话,时间就肯定会超时，所以暴力解法不可行。

那么我们现在来看有没有更加省时间的方式：

       首先，我们可以确定的是，类似于暴力解法，我们寻找一个元素的左边第一个比它小的元素，假设当前我们要寻找下标为i处的数的左边第一个比它小的数，那么我们就需要在区间[0,i-1]内遍历进行答案的寻找，这个过程是比较麻烦的，我们能不能采取一种方式，能够将上一次的寻找结果中的无用的值去掉以减少搜索呢？答案肯定是可行的。下面我们来简单推导一下：

        我们现在所担心的就是，前面的保存的解会不会导致后面的检索出现错误的情况，也就是说，前面的解能否正确的给出后面的寻找答案；

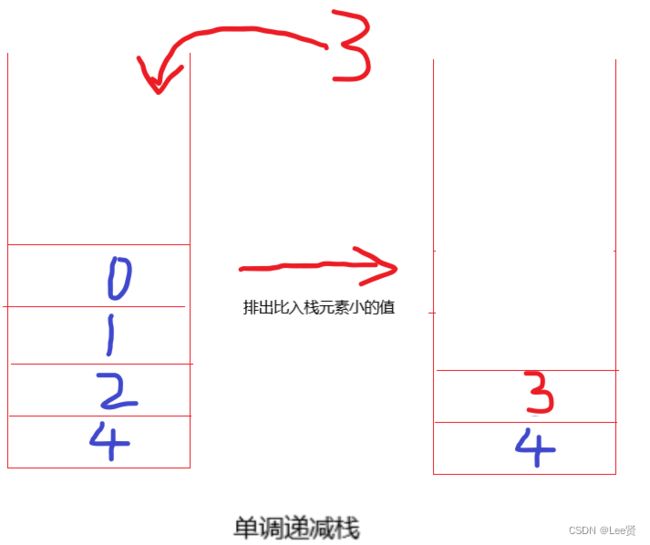
        1.单调栈是单调递减或者点掉递增的栈结构，每次入栈需要和栈内的元素作对比，将栈内的元素大于（单调递减栈）或者小于（单调递增栈）将要入栈的元素的元素给删掉以保持其单调特性不被破坏，这也是单调栈的核心思路；

          2.单调栈的特性，让我们可以保存上一次寻找的结果的同时，将本次寻找的下标所代表的元素入栈，可以在下次寻找时，再次按照需要恢复单调栈的方式更新栈，栈顶元素或者栈为空就是当前元素的寻找结果，并且如此做，保证了，每次的最小值都会保存在栈顶中，也能够确保结果的正确性。

所以，上述的例题，采用单调栈的方式可以如下图：

 有了上面的知识，我们可以来尝试构建代码了：

#include
#include 
using namespace std;
const int maxm=100010;
int n;
int a[maxm];
stack st;
int res[maxm];
int main()
{
    scanf("%d",&n);
    for(int i=0;i=a[i])//将大于a[i]的栈内的元素删掉
             st.pop();
        if(!st.empty())//如果栈内还有元素，那么一定是a[i]的左侧第一个比a[i]小的数了
           res[i]=st.top();
        else
           res[i]=-1;//如果栈空了,说明没有找到
        st.push(a[i]);//最后，我们需要将a[i]入栈，以保证后续的更新栈和寻找结果正确性
    }
    for(int i=0;i

1.2 单调栈-下标作为栈元素

       有时候，我们需要的不是返回某个数的左侧或者右侧的第一个小或者大的数本身，而是返回该数所在的下标，那么我们就可以将对应的数的下标进行入栈，本质上是一样的，就是换了个考察方式而已。

输入样例：

6 
3 
2 
6 
1 
1 
2 

输出样例：

3 
3 
0 
6 
6 
0 

对于如何确定单调递减栈还是单调递增栈：

       区间最值问题

解决区间最值问题时，需要使用单调栈。对于求解具体的区间最值问题，可以考虑如下方法：

• 对于求解区间最大值问题，可以建立单调递减栈。如此，栈中的元素都是单调递减的，满足任意元素与当前元素组成区间时，当前元素为区间最大值。
• 对于求解区间最小值问题，可以建立单调递增栈。如此，栈中的元素都是单调递增的，满足任意元素与当前元素组成区间时，当前元素为区间最小值。

      贪心算法问题

      贪心算法中，需要对数据进行逐步筛选或选择，以达到期望的最优化。在这类问题中，通常需要保证当前处理的数据与之前处理的数据保持单调性。如果当前数据与之前处理的数据单调递增，可以建立单调递增栈。反之，如果单调递减，可以建立单调递减栈。一般来说，需要的元素是比某个元素更大的，就让努力让栈顶的元素保持最大，反之亦然。

       从上述我们可以知道，右侧的更高的牛和左侧的矮一些的牛呈单调递增，也就是说，我们需要的是一个元素右侧对应的下一个更高的，所以我们需要保证更高的栈顶，所以说我们需要建立单调递增栈，第二，处理编号问题，我们可以用单调栈存储元素的值改为存储元素的下标即可。

#include
#include 
using namespace std;

const int maxm=1e6+5;
int h[maxm];
int n;
stackm;
int res[maxm];
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
      scanf("%d",&h[i]);
    for(int i=n;i>=1;i--)
    {
        while(!m.empty()&&h[m.top()]<=h[i])//现在的栈中储存的是数对应的下标,当前元素比栈顶元素大时，我们需要将小的元素出栈，来找到大的元素
             m.pop();
        if(!m.empty())
           res[i]=m.top();//最终结果是元素对应的下标
        else
           res[i]=0;
        m.push(i);//这次我们需要将元素对应的编号入栈
    }
    for(int i=1;i<=n;i++)
      printf("%d\n",res[i]);
    return 0;
}

1.3总体区间最值问题 

输入样例：

12
0 1 0 2 1 0 1 3 2 1 2 1

输出样例：

6

 思路分析：

1.单调递减栈的建立

          由题意，我们知道需要求解积水量，而我们每读入一个元素的高度，需要向左找到第一个大于该元素的下标位置处，两者之间才能形成积水区域，所以我们需要建立的是一个单调递减栈，每次可以通过新的元素入栈而找出与该高度左侧的可能形成的“坑”的面积，从而求出积水量。

2.积水面积的计算

          该题我们还是利用单调栈，在每一个高度入栈时，用单调栈找每个障碍物左边第一个比它高的位置，累加两障碍物之间的储雨量，注意最后栈内元素是呈降序排列的。字不如图，我们来画图分析：

#include
#include
using namespace std;
const int maxm=100005;

int n;//个数
int h[maxm];
stack idx;//这个栈用来保存下标
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
      scanf("%d",&h[i]);
    int ans=0;//保存最后的结果
    for(int i=1;i<=n;i++)
    {
        //我们首先需要找到一个满足能形成“坑”的位置，也就是某个位置的前面存在比它低的位置处，这里我们的单调栈是单调递减的,我们按栈内的元素向前查找，如果找到了比当前元素矮的
        int bottom=0;//我们按层次来计算每一层的积水量
        while(!idx.empty()&&h[idx.top()]

1.4部分区间最值问题

输入样例：

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

输出样例：

8
4000

 解题思路：

1.如何判断由某一个基准矩形快所构成的最大矩形的面积

       我们需要首先来分析对于其中的一小块矩形块，我们如何求解由该矩形块和其他的矩形块所构成的最大的连通的矩形的面积，这里可能会存在两种情况：

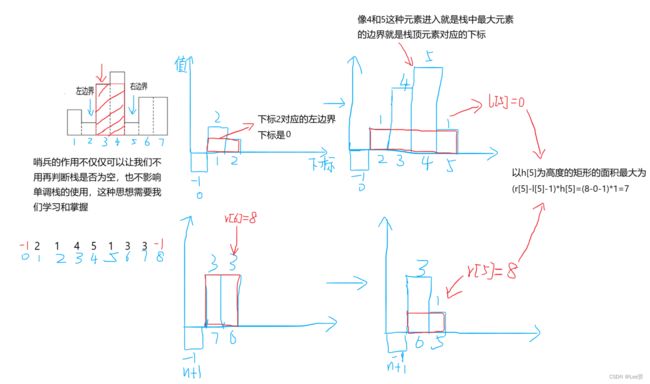
        可见，对于每一个基准块来说，小于其高度所形成的最大矩形面积可以由其他的较矮的矩形块求出，而上述的红色区域的面积却因为受基准块高度的限制而只能求解一次，所以，本着宁可错选而不漏选的原则，我们在由一个基准块求解其所能构成的最大矩形的面积的时候，我们需要将该矩形块的高度看做限制条件，只要左右两侧的矩形块的高的比它矮，我们就找到了该矩形块的边界，这样我们边可以和单调递增栈结合起来，相当于找到一个元素对应的左侧和右侧的第一个比该元素小的值，也就找到了左右边界，矩形面积也就可以求出来了。

2.数组模拟单调栈以及哨兵位的设置省去判断栈为空和边界情况

     前面我们的单调栈的例题中，需要对每一的高度判断栈是否为空，在本题中，我们可以采用数组模拟栈，我们可以加入哨兵位来让栈中永远都有元素，而这个元素需要根据题意来设计，这里我们在不影响答案求解的情况下，可以将哨兵位设在0和n+1的下标处（高度存储是从下标1开始的），因为我们需要的是一个能够找到左右两侧第一个比待选元素小的元素，所以我们需要一个单调递增栈，所以我们设h[0]=h[n+1]=-1(只要比题目中的任何高度都小就行）来保证栈底始终存在元素-1即可。然后我们就可以按照求解左右侧第一个小于元素的模式来解题。

代码实现：

#include 
using namespace std;

const int maxm=100010;
int n;
int h[maxm],l[maxm],r[maxm];//其中l和r数组分别代表在下标位置为i处的左边界和右边界
int q[maxm];//数组模拟栈

int main()
{
    while(scanf("%d",&n),n)//逗号表达式,取最后一项的值
    {
        for(int i=1;i<=n;i++)
            scanf("%d",&h[i]);
        h[0]=h[n+1]=-1;//左右设置两个虚拟的哨兵，可以不用判断越界或者栈为空的情况
        int tt=0;
        q[tt]=0;
        for(int i=1;i<=n;i++)
        {
            while(h[q[tt]]>=h[i]) tt--;//向左侧找到以h[i]为高度的左边界（也就是第一个小于h[i]的位置处
            l[i]=q[tt];
            q[++tt]=i;//将新的下标入栈
        }
        
        tt=0;//清空栈
        q[tt]=n+1;//末尾的虚拟下标入栈（为了防止栈为空)
        for(int i=n;i>=1;i--)
        {
            while(h[q[tt]]>=h[i]) tt--;
            r[i]=q[tt];
            q[++tt]=i;
        }
        long long  res=0;//可能会爆int，数据范围开大些
        for(int i=1;i<=n;i++)
        {
            res=max(res,(long long)h[i]*(r[i]-l[i]-1));
        }
        printf("%lld\n",res);
    }
    return 0;
}

2.单调队列 

单调队列是一种队列，它同样保持单调递增或单调递减。使用单调队列的场景包括：

• 在一个滑动窗口中求解最值问题。
• 求解图中的最短路径问题。

单调队列可以在O(n)时间内解决上述问题，而使用普通的算法可能需要O(n^2)的时间复杂度。

2.1 单调队列的例题引入

 

输入样例：

8 3
1 3 -1 -3 5 3 6 7

输出样例：

-1 -3 -3 -3 3 3
3 3 5 5 6 7

我们还是从暴力解法中寻找可以优化的点，我们现在单独拿最大值来看：

由于我们需要求出的是滑动窗口的最大值。

       如果当前的滑动窗口中有两个下标 i 和 j ，其中i在j的左侧（i

       当滑动窗口向右移动时，只要 i 还在窗口中，那么 j 一定也还在窗口中。这是由于 i 在 j 的左侧所保证的。

        因此，由于 nums[j] 的存在，nums[i] 一定不会是滑动窗口中的最大值了，我们可以将nums[i]永久地移除。

        因此我们可以使用一个队列存储所有还没有被移除的下标。在队列中，这些下标按照从小到大的顺序被存储，并且它们在数组nums中对应的值是严格单调递减的。

        当滑动窗口向右移动时，我们需要把一个新的元素放入队列中。为了保持队列的性质，我们会不断地将新的元素与队尾的元素相比较，如果新元素大于等于队尾元素，那么队尾的元素就可以被永久地移除，我们将其弹出队列。我们需要不断地进行此项操作，直到队列为空或者新的元素小于队尾的元素。

        由于队列中下标对应的元素是严格单调递减的，因此此时队头下标对应的元素就是滑动窗口中的最大值。

代码实现：

#include

using namespace std;

const int maxm=1000010;
int n,k;
int a[maxm],q[maxm];//数组和q模拟单调队列,注意q中存储的是下标

int main()
{
    scanf("%d%d",&n,&k);
    for(int i=0;iq[st])//大于说明保存长度为k的队列就要向右移动，且一次移动一个位置
           ++st;
        while(st<=ed&&a[q[ed]]>=a[i])//目的是找到当前队列中的最小的值将其置为队尾 
           --ed;
        q[++ed]=i;//新的下标入队
        if(i+1 >= k)//说明满k个可以输出了
           printf("%d ",a[q[st]]);
        
    }
    printf("\n");
    st=0,ed=-1;
    for(int i=0;iq[st]) ++st;
        while(st<=ed&&a[q[ed]]<=a[i]) --ed;
        q[++ed]=i;
        if(i+1 >= k)
          printf("%d ",a[q[st]]);
    }
   
    return 0;
}

2.2区间最值问题

思路分析：

前缀和：

       前缀和的基本思想是，预处理一个数组 Sum，其中 Sum[i] 表示 num[0] + num[1] + … + num[i-1]（也就是前 i 个元素的和），那么 num[i] 到 num[j] 的区间和就可以通过计Sum[j+1] - Sum[i] 得出。这样以来，我们可以在 O(n) 的时间复杂度内计算出整个数组的前缀和，并且前缀和数组可用于 O(1) 的时间复杂度内计算任意区间的和。实际中为了方便，我们一般都是将数组从下标1开始存数，这样前缀和的下标和数组的下标就能更好的对应起来。

那么这道题目如何处理呢？

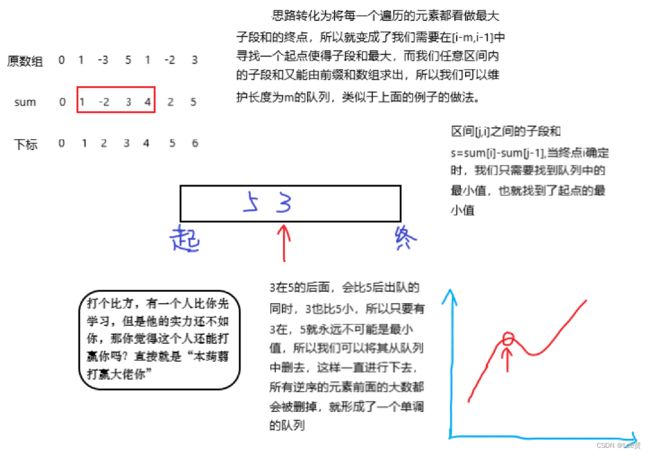
        我们发现我们的目标就是找到两个位置l, r 满足要求 r−l≤m 也就是说区间的大小不可以超过m
sum[r]−sum[l]尽量大.
        这么说来，我们完全可以O(n^2)枚举l, r不就好了吗？但是时间上肯定是做不到的，所以我们尝试着用单调队列来进行优化：

 代码如下：

#include 
using namespace std;

const int maxm=300010;
int n,m;
int s[maxm],q[maxm];//前缀和数组s和q数组模拟队列

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&s[i]);
        s[i]+=s[i-1];//直接求前缀和数组，原数组对我们是无用的，所以我们可以直接对其修改为前缀和数组s
    }
    
    int st=0,ed=0;//队头队尾赋初值
    int res=INT_MIN;//保存最大子段和
    for(int i=1;i<=n;i++)
    {
        if(i-q[st]>m) st++;//队头出队,注意这里其实是让队列中保持m+1个元素，因为我们的队头元素必须是sum[j-1]，[i,j]前缀和，计算必须用到sum[j-1]，而不是sum[j]
        //去除逆序的元素并计算最优值
        res=max(res,s[i]-s[q[st]]);
        //去除逆序的元素，使队列再次单调
        while(st<=ed&&s[q[ed]]>=s[i]) --ed;
        //加入当前元素
        q[++ed]=i;
    }
    printf("%d\n",res);
    return 0;
}

       

         关于单调队列的联系，个人还有待进一步加强，后续也会继续更新相关的内容，文章内容较多，所以这里就不再详述了。

3.金句频道

        千万别用年轻时的懒惰和放纵，换来一生的后悔，因为，我们现在的努力里，藏着我们十年后的样子，凡事想着蒙混过关，“摸鱼划水”，困难只会越来越多。