2023杭电 “钉耙编程”中国大学生算法设计超级联赛（2）补题

Alice Game  Nim博弈与SG函数打表

Binary Number 结论构造，思维，细节模拟

Card Game 签到，快速幂

foreverlasting and fried-chicken 组合数学，bitset优化，细节

String Problem 签到，字符串模拟

Klee likes making friends DP，取模优化与后缀优化

SPY finding NPY 概率论，组合数学

Coin 网络流建图，最大流

 Problem - 7287

本题第一条操作有歧义，正确意思应该是只有长度小于等于K的时候才能用第一个操作。这一操作仅仅用于初始化SG函数。

SG函数中  mex用于 求全部后继状态SG函数的mex得出本次的SG函数

而异或用于 子问题 即子问题的SG函数异或得出本次SG函数

本题中，一个长度大于k的中间被横切一刀，产生两端，这两端为 “子问题”，而横切一刀产生的全部左右搭配，称作“后继状态”。 所以我们要对全部后继状态求mex,而后继状态的SG函数，就是俩子问题的SG函数异或值。

最终打表不难发现，SG函数为0的点呈现周期律

# include
using namespace std;
typedef long long int ll;
# define mod 998244353
int sg[1010],n,k;
int  getsg(int now)
{

    if(sg[now]!=-1)
        return sg[now];
    sets;

    for(int i=1;i<=now;i++)
    {
        int left=i,right=now-i-k;
        if(left>0&&right>0)
            s.insert(getsg(left)^getsg(right));
    }
    int ans=0;
    while(s.count(ans))
    {
        ans++;
    }
    return sg[now]=ans;
}
int main ()
{
    //打表

    memset(f,-1,sizeof(f));

    int n,k;
    cin>>n>>k;
    for(int i=1;i<=k;i++)
    {
       sg[i]=1;

    }
    for(int i=1;i<=n;i++)
    {
        cout<>t;
    while(t--)
    {
        ll k,n;
        cin>>k>>n;
         ll t=4ll*k+2;
        if(n<=k)
        {
            cout<<"Alice"<0&&(cha)%t==0)
            {
                cout<<"Bob"<

Problem - 7288

 

本题应该是个构造题。

首先看01分段后，0全部变成1的情况，加入0的段数小于等于k,显然从前往后即可。

一旦k等于0的段数+1时，难道真的是把最后一个翻转为1就最优了吗？答案是不对的。

考虑这样一种情况，即01交界或10交界。以01交界为例

01-> 00->11 共翻转两次

所以，当我们k=cnt0+1时，不妨把之前修改一段0的操作给吐出来，现在剩余两次，对01或者10进行两次操作即可。

k=cnt0+2，恰好偶数次，故不需要构造。

所以我们可以得出结论，在s[1]=1的已知条件下，只要有0存在，就一定能够变成全1

另外就是1变成0到底能不能比0变成1更优？

首先1段数应该是大于等于0段数的，当k>=cnt0时，显然变1不会更优，当k

另外就是细节特判。全是1的情况，k=1,n=1等极端情况。

# include
using namespace std;
typedef long long int ll;
# define mod 998244353

int main ()
{
    int t;
    cin>>t;

    while(t--)
    {
        int n;
        ll k;
        cin>>n>>k;
        string s;
        cin>>s;
        s=" "+s;
        if(n==1)
        {
            if(k%2==1)
            {
                cout<<0<<'\n';
            }
            else
            {
                cout<<1<<'\n';
            }
        }
        else  if(k==0)
        {
            for(int i=1; i<=n; i++)
            {
                cout<

 Problem - 7290

没什么好说的，直接快速幂 

# include
using namespace std;
typedef long long int ll;
# define mod 998244353
ll qp(ll base, ll pow)
{
    ll ans=1;
    while(pow)
    {
        if(pow&1)
            ans=ans*base%mod;
        pow>>=1;
        base=base*base%mod;
    }
    return ans;
}
int main ()
{

    int t;
    cin>>t;
    while(t--)
    {
        int n;
        cin>>n;

        cout<<((qp(2ll,n-1)-1)%mod+mod)%mod<<'\n';
    }

    return 0;
}

Problem - 7293

首先这一模型是由一个度数至少为6的上部点和与上部点相交至少4点的下部点构成。考虑n^2枚举上下部点。至于相交的快速判断，用bitset优化即可。

一旦找到满足的上下点，C(cnt,4)*C(du-4,2)为当前贡献。即从全部相交点抽出4个，从全部度数点里面，再抽出2个

特别的，当上部点和下部点直接相连的时候，对cnt没有影响，但对上部点度数有直接影响，故特判使之度数-1

# include
using namespace std;
typedef long long int ll;
vectorv[1010];
bitset<1010>s[1010];
ll fac[1010],inv[1010];
int du[1010];
# define mod  1000000007
inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while (!isdigit(ch))
    {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (isdigit(ch))
    {
        x = (x << 1) + (x << 3) + (ch ^ 48);
        ch = getchar();
    }
    return x * f;
}

inline void write(ll x)
{
    if (x < 0)
        putchar('-'), x = -x;
    if (x > 9)
        write(x / 10);
    putchar(x % 10 + '0');
}
ll qp(ll base, ll pow)
{
    ll ans=1;
    while(pow)
    {
        if(pow&1)
            ans=ans*base%mod;
        pow>>=1;
        base=base*base%mod;
    }
    return ans;
}
void init()
{
    fac[0]=1;
    for(ll i=1; i<=1000; i++)
        fac[i]=fac[i-1]*i%mod;

    inv[1000]=qp(fac[1000],mod-2);
    for(ll i=1000-1; i>=0; i--)
        inv[i]=inv[i+1]*(i+1)%mod;
    return ;
}
ll getc(int x,int y)
{
    if(x>t;
    init();

    while(t--)
    {
        int n,m;
        scanf("%d%d",&n,&m);
        for(int i=1; i<=n; i++)
        {
            du[i]=0;
            v[i].clear();
            s[i].reset();
        }
        for(int i=1; i<=m; i++)
        {
            int x,y;
           x=read();
           y=read();
            du[x]++;
            du[y]++;
            v[x].push_back(y);
            v[y].push_back(x);
            s[x][y]=1;
            s[y][x]=1;
        }

        ll ans=0;
        for(int up=1; up<=n; up++)
        {
            if(du[up]<6)
                continue;
            for(int down=1; down<=n; down++)
            {
                if(up==down)
                    continue;
                bitset<1010>now=(s[up]&s[down]);
                int cnt=now.count();
                int nowdu=du[up];
                if(s[up][down])
                    nowdu--;
                if(cnt>=4)
                {
                    ans+=getc(cnt,4)*getc(nowdu-4,2)%mod;

                    ans%=mod;
                }
            }
        }
        cout<

Problem - 7295

没什么说的，阅读题目全面即可 

#include
using namespace std;
typedef long long int ll;
# define mod 998244353

int main()
{

     int t;
     cin>>t;
     while(t--)
     {
         string s;
         cin>>s;
         int ans=0;

         for(int i=0;i

 Problem - 7296

  

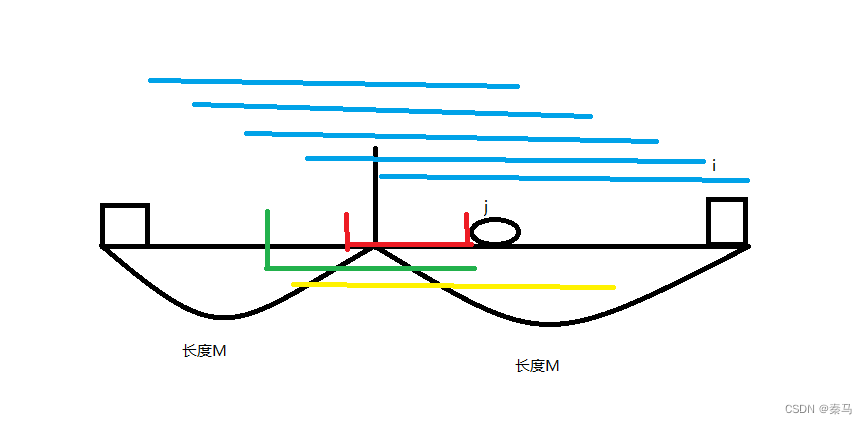
dp[i][j]代表当前选i,前面距离i最近的一个点备选，距离为j, 首先这些点是在i距离m范围内选取。而j之前一个点的选取，是有要求的。如果简单粗暴选取j之前m范围内的任意点，即图中绿色部分，会导致图中黄色部分（长度m）只有一个j点被选取。而如果j之前一点定在红色区域，就不会出现这样的情况。 即在j之前已经满足情况下，新开i点带来的全部蓝色区域，都是满足有两个的。

这样来看，满足条件的j在im范围内，而j之前的点也是有一个范围，[1,j-(i-m)]，这个可以用一个连续转移的前缀最小值来实现。

# include
using namespace std;
typedef long long int ll;
ll dp[2020][2020],minn[2020][2020],a[200000+10];
int pos[200000+10];
int main()
{

    int t;
    cin>>t;

    while(t--)
    {
        int n,m;
        cin>>n>>m;
        for(int i=0; i<=m; i++)
        {
            for(int j=0; j<=m; j++)
            {
                minn[i][j]=1e18;
                dp[i][j]=1e18;
            }
        }
        for(int i=1; i<=n; i++)
        {
            scanf("%lld",&a[i]);
            pos[i]=i%m;
        }
        for(int i=2; i<=m; i++)
        {
            for(int j=i-1; j>=1; j--)
            {

                dp[pos[i]][i-j]=a[i]+a[j];
                minn[pos[i]][i-j]=min(dp[pos[i]][i-j],minn[pos[i]][i-j-1]);

            }
        }

        for(int i=m+1; i<=n; i++)
        {
            for(int j=i-1; j>=i-m+1; j--)
            {
                dp[pos[i]][i-j]=a[i]+minn[pos[j]][j-(i-m)];
                minn[pos[i]][i-j]=min(dp[pos[i]][i-j],minn[pos[i]][i-j-1]);
            }
        }
        ll ans=1e18;

        for(int i=n; i>=n-m+2; i--)
        {
            for(int j=i-1; j>=n-m+1; j--)
            {
                ans=min(ans,dp[pos[i]][i-j]);
            }
        }
        cout<

 Problem - 7297

首先，在第k局能赢的全部情况是，最大值n在k位置，k+1位置，...n位置，且在[1,最大值位置-1]的这些数字，里面的最大值必须在[1,k]就被提前选到，否则，他会在n之前被选到 。

那么现在就变成了，对求解，也就是把k/n提出来，直接前缀和搞，暴力枚举即可。不需要三分或者数学知识。

#include 
# include

using namespace std;
const int N = 1e4 + 5;
const double E = exp(1);
double sum[N];

double calc(int n, int k)
{
    if (k == 0) return 1.0 / n;
    return 1.0 * k / n * (sum[n - 1] - sum[k - 1]);
}

void work()
{
    int n;
    cin >> n;
    int l = 0, r = n - 1;
    int ans = -1;
    double p = -1;
    for (int i = l; i <= r; ++i)
    {
        double now = calc(n, i);
        if (now > p)
        {
            p = now;
            ans = i;
        }
    }
    cout << ans << "\n";
}

int main()
{
    for (int i = 1; i < N; ++i) sum[i] = sum[i - 1] + 1.0 / i;
    int T;
    cin >> T;
    while (T--)
    {
        work();
    }
    return 0;
}

Problem - 7298

首先操作有次序，这就否决掉了只拆一次点建图的方案，这样次序无法保证。故采用最原始的，每次操作就进行拆点的建图方式，建立n*m个点，点和点之间连ai,但很显然会导致图过大。 考虑，只有操作时才拆点，这样既能保证次序，还能保证不会过大。

#include
# include
# include
using namespace std;
typedef long long int ll;
typedef struct
{
    int b,e;
    ll val;
} xinxi;
xinxi s[101010];
int f[101010],nex[101010],len=2,n,m,dep[101010],st,ed;
int tot;
void add(int x,int y,ll z)
{
    s[len].b=x;
    s[len].e=y;
    s[len].val=z;
    nex[len]=f[x];
    f[x]=len;
    len++;
}
queueQ;
bool bfs()
{
    memset(dep,0,sizeof(dep));
    Q.push(st);
    dep[st]=1;
    while(!Q.empty())
    {
        int u=Q.front();
        Q.pop();

        for(int i=f[u]; i!=-1; i=nex[i])
        {
            int v=s[i].e;
            if(dep[v]==0&&s[i].val)
            {
                dep[v]=dep[u]+1;
                Q.push(v);
            }
        }
    }
    return dep[ed];
}
ll dfs(int now,ll flow)
{
    if(now==ed)
        return flow;
    ll out=0;
    int x=f[now];
    while(x!=-1)
    {
        int j=s[x].e;

        if(dep[j]==dep[now]+1&&s[x].val)
        {
            ll temp=dfs(j,min(flow,s[x].val));
            s[x].val-=temp;
            s[x^1].val+=temp;
            flow-=temp;
            out+=temp;
        }

        if(!flow)
            break;
        x=nex[x];

    }
    if(!out)
        dep[now] = 0;
    return out;


}
int last[200000+10];
int a[200000+10];
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        len=2;
        memset(f,-1,sizeof(f));
        int n,m,k;
        scanf("%d%d%d",&n,&m,&k);
        tot=0;
        st=0;
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&a[i]);
            tot++;
            add(st,tot,1);
            add(tot,st,0);
            last[i]=tot;

        }
        for(int i=1;i<=m;i++)
        {
            int x,y;
            scanf("%d%d",&x,&y);
            tot++;
            add(last[x],tot,a[x]);
            add(tot,last[x],0);
            last[x]=tot;
            tot++;
            add(last[y],tot,a[y]);
            add(tot,last[y],0);
            last[y]=tot;

            add(last[x],last[y],1);
            add(last[y],last[x],0);
            add(last[y],last[x],1);
            add(last[x],last[y],0);

        }
        tot++;
        ed=tot;
        for(int i=1;i<=k;i++)
        {
            int x;
            scanf("%d",&x);
            add(last[x],ed,a[x]);
            add(ed,last[x],0);
        }
        ll ans=0;

        while(bfs())
        {
            ans+=dfs(st,1e18);
        }

        cout<