利用C语言实现页面置换算法

操作系统实验

页面置换算法（FIFO、LRU、OPT）

概念：

1.最佳置换算法（OPT）（理想置换算法）：从主存中移出永远不再需要的页面；如无这样的页面存在，则选择最长时间不需要访问的页面。于所选择的被淘汰页面将是以后永不使用的，或者是在最长时间内不再被访问的页面，这样可以保证获得最低的缺页率。
2.先进先出置换算法（FIFO）：是最简单的页面置换算法。这种算法的基本思想是：当需要淘汰一个页面时，总是选择驻留主存时间最长的页面进行淘汰，即先进入主存的页面先淘汰。其理由是：最早调入主存的页面不再被使用的可能性最大。
3．最近最久未使用（LRU）算法：这种算法的基本思想是：利用局部性原理，根据一个作业在执行过程中过去的页面访问历史来推测未来的行为。它认为过去一段时间里不曾被访问过的页面，在最近的将来可能也不会再被访问。所以，这种算法的实质是：当需要淘汰一个页面时，总是选择在最近一段时间内最久不用的页面予以淘汰。

题目：

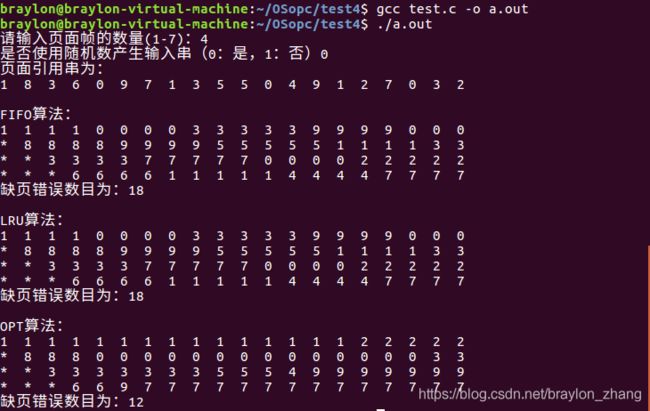
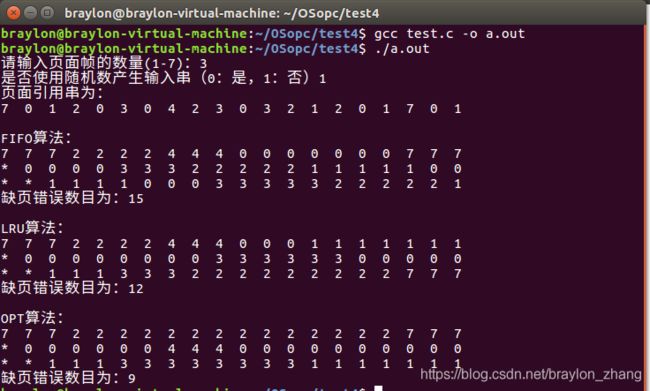
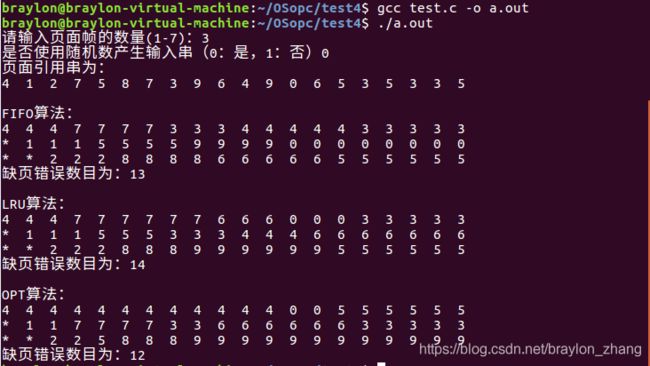
编写一个程序，实现本章所述的FIFO、LRU和最优页面置换算法。首先，生成一个随机的页面引用串，其中页码范围为0-9.将这个随机页面引用串应用到每个算法，并记录每个算法引起的缺页错误的数量。实现置换算法，一遍页面帧的数量可以从1~7。

代码

#include 
#include 
#include 

int numbers[20]={7,0,1,2,
                 0,3,0,4,
                 2,3,0,3,
                 2,1,2,0,
                 1,7,0,1};//本地数据，与课本一致，方便测试
int nums=0;//输入栈的个数，为了方便使用，
int stack[20][7]={10};

void begin();
void randomnum();//用于产生随机数
void init();//初始化
void FIFO();//FIFO算法
void LRU();//LRU算法
void OPT();//最优页面置换算法（OPT）
void print();//输出

int main() {
    begin();
    FIFO();
    LRU();
    OPT();
    return 0;
}
void begin()//开始菜单界面
{
    int i,j,k;
    printf("请输入页面帧的数量(1-7)：");
    scanf("%d",&nums);
    for(k=0;;k++)
    {
        printf("是否使用随机数产生输入串（0：是，1：否）");
        scanf("%d",&j);
        if(j==0)
        {
            randomnum();
            break;
        }
        else if(j==1)
        {
            break;
        }
        else
        {
            printf("请输入正确的选择！\n");
        }
    }

    printf("页面引用串为：\n");
    for(i=0;i<20;i++)
    {
        printf("%d  ",numbers[i]);
    }
    printf("\n");
    init();
}
void randomnum()//如果需要使用随机数生成输入串，调用该函数
{
    srand(time(0));//设置时间种子
    for(int i = 0; i < 20; i++) {
        numbers[i] = rand() % 10;//生成区间0`9的随机页面引用串
    }
}
void init()//用于每次初始化页面栈中内容，同时方便下面输出的处理
{
    int i,j;
    for(i=0;i<20;i++)
        for(j=0;j<nums;j++)
            stack[i][j]=10;
}

void print()//输出各个算法的栈的内容
{
    int i,j;
    for(i=0;i<nums;i++)
    {
        for(j=0;j<20;j++)
        {
            if(stack[j][i]==10)
                printf("*  ");
            else
                printf("%d  ",stack[j][i]);
        }
        printf("\n");
    }

}

void FIFO()//FIFO算法
{
    init();
    int i,j=1,n=20,k,f,m;
    stack[0][0]=numbers[0];

    for(i=1;i<20;i++)
    {
        f=0;
        for(m=0;m<nums;m++)
        {
            stack[i][m]=stack[i-1][m];
        }
        for(k=0;k<nums;k++)
        {
            if(stack[i][k]==numbers[i])
            {
                n--;
                f=1;
                break;
            }
        }
        if(f==0)
        {
            stack[i][j]=numbers[i];
            j++;
        }
        if(j==nums)
            j=0;
    }
    printf("\n");
    printf("FIFO算法：\n");
    print();
    printf("缺页错误数目为：%d\n",n);
}

void LRU()//LRU算法
{
    int i,j,m,k,sum=1,f;
    int sequence[7]={0};//记录序列
    init();
    stack[0][0]=numbers[0];
    sequence[0]=nums;
    for(i=1;i<nums;i++)//前半部分，页面空置的情况
    {
        for(j=0;j<nums;j++)
        {
            stack[i][j]=stack[i-1][j];
        }

        for(j=0;j<nums;j++)  //判断要插入的是否在栈中已经存在
        {
            f=0;
            if(stack[i][j]==numbers[i])
            {
                f=1;
                sum--;
                sequence[j]=nums;
                break;
            }
        }

        for(j=0;j<nums;j++)
        {
            if(sequence[j]==0&&f==0)
            {
                stack[i][j]=numbers[i];
                sequence[i]=nums;//最近使用的优先级列为最高
                break;
            }
        }
        for(j=0;j<i;j++)//将之前的优先级序列都减1
        {
            if(sequence[j]!=0)
               sequence[j]--;
        }
        //sequence[i]=nums;
        sum++;
    }

    for(i=nums;i<20;i++)//页面不空，需要替换的情况
    {
        int f;
        f=0;
        for(j=0;j<nums;j++)
        {
            stack[i][j]=stack[i-1][j];
        }
        for(j=0;j<nums;j++)//判断输入串中的数字，是否已经在栈中
        {
            if(stack[i][j]==numbers[i])
            {
                f=1;
                k=j;
                break;
            }
        }
        if(f==0)//如果页面栈中没有，不相同
        {
            for(j=0;j<nums;j++)//找优先序列中为0的
            {
                if(sequence[j]==0)
                {
                    m=j;
                    break;
                }
            }
            for(j=0;j<nums;j++)
            {
                sequence[j]--;
            }
            sequence[m]=nums-1;
            stack[i][m]=numbers[i];
            sum++;
        }
        else//如果页面栈中有，替换优先级
        {
           if(sequence[k]==0)//优先级为最小优先序列的
           {
               for(j=0;j<nums;j++)
               {
                   sequence[j]--;
               }
               sequence[k]=nums-1;
           }
           else if(sequence[k]==nums-1)//优先级为最大优先序列的
           {
               //无需操作
           }
           else//优先级为中间优先序列的
           {
               for(j=0;j<nums;j++)
               {
                   if(sequence[k]<sequence[j])
                   {
                       sequence[j]--;
                   }
               }
               sequence[k]=nums-1;
           }
        }
    }
    printf("\n");
    printf("LRU算法：\n");
    print();
    printf("缺页错误数目为：%d\n",sum);
}

void OPT()//OPT算法
{
    int i,j,k,sum=1,f,q,max;
    int seq[7]={0};//记录序列
    init();
    stack[0][0]=numbers[0];
    seq[0]=nums-1;

    for(i=1;i<nums;i++)//前半部分，页面空置的情况
    {
        for(j=0;j<nums;j++)
        {
            stack[i][j]=stack[i-1][j];
        }

        for(j=0;j<nums;j++)  //判断要插入的是否在栈中已经存在
        {
            f=0;
            if(stack[i][j]==numbers[i])
            {
                f=1;
                sum--;
                //b++;
                seq[j]=nums;
                break;
            }
        }

        for(j=0;j<nums;j++)
        {
            if(seq[j]==0&&f==0)
            {
                stack[i][j]=numbers[i];
                seq[j]=nums;//最近使用的优先级列为最高
                break;
            }
//            else if(seq[j]==0&&f==1){
//                b++;
//                sum--;
//                seq[j]=nums-1;
//                break;
//            }
        }
        for(j=0;j<nums;j++)//将之前的优先级序列都减1
        {
            if(seq[j]!=0)
               seq[j]--;
        }

        sum++;
    }
    for(i=nums;i<20;i++)//后半部分，页面栈中没有空的时候情况
    {
        //k=nums-1;//最近的数字的优先级
        for(j=0;j<nums;j++)//前面的页面中内容赋值到新的新的页面中
        {
            stack[i][j]=stack[i-1][j];
        }
        for(j=0;j<nums;j++)
        {
            f=0;
            if(stack[i][j]==numbers[i])
            {
                f=1;
                break;
            }
        }
        if(f==0)//页面中没有，需要替换的情况
        {
            for(q=0;q<nums;q++)//优先级序列中最大的就是最久不会用的，有可能出现后面没有在用过的情况
            {
                seq[q]=20;
            }
            for(j=0;j<nums;j++)//寻找新的优先级
            {
                for(q=i+1;q<20;q++)
                {
                    if(stack[i][j]==numbers[q])
                    {
                        seq[j]=q-i;
                        break;
                    }
                }
            }
            max=seq[0];
            k=0;
            for(q=0;q<nums;q++)
            {
                if(seq[q]>max)
                {
                    max=seq[q];
                    k=q;
                }
            }
            stack[i][k]=numbers[i];
            sum++;
        }
        else
        {
            //页面栈中有需要插入的数字，无需变化，替换的优先级也不需要变化
        }
    }
    printf("\n");
    printf("OPT算法：\n");
    print();
    printf("缺页错误数目为：%d\n",sum);
}

运行结果截图：

总结

设置多个数组，一个用来模仿栈，一个用来存要存取的页面，还有在OPT算法和LRU算法中，记录栈中每个数据的替换优先级。
之前的代码写的有点烂，重新看了一次才感觉之前的有多烂，哈哈哈哈哈，这个代码能在linux上跑通的，在windows上肯定也没得问题