小白学算法:DFS排列组合问题
准备:
一些用语及事项的说明,方便大家理解。
1.数组从一号索引开始用,不用0号索引。
2.dfs递归零次时称为深度1,递归一次称为深度2,以此类推。
3.每个深度dfs要进行一些操作,统称某深度运算空间中的计算。
4.以图的遍历讲解组合排列的求解
排列
问题:给定一个含有n个元素的数表,从中选定k个数,可以构成多少种排列
输出每种排列 和总的排列 数,每个数三个场宽。
上代码:
#include 组合
数的组合问题:
给定一个含有n个元素的数表,从中选定k个数,可以构成多少个组合
输出每种组合和总的组合数,每个数三个场宽
上代码:
#include 分析
分析的重点在于,这两个代码不同的原因。通过探究原因,深入理解循环和哨兵的作用。
我们很容易看出来,这两份代码的差异所在:
1.循环的起点不同。
2.一个使用了哨兵,一个没有使用。
下面我们通过图来探究他们不同的原因。
问题引入:我们将排列组合的问题,放在图中思考。如下图;
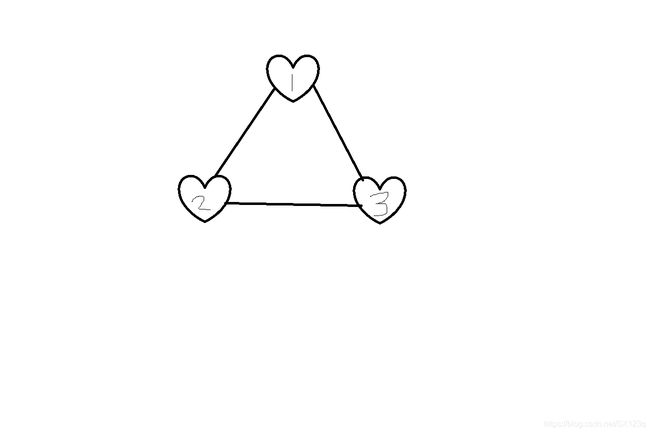
问题一,分析排列
问题:在图中的3个元素中,任意选取两个元素构成一个排列,总共有多少种选项方案?
解决:
第一步:当我们从 1 开始走的时候,我们可以得到 12 和13两种排列。
第二步:当我从2开始走的时候,依照排列的原则,我可以有21和23两种排列方案。
那么问题来了(记为问题X):
当我从2开始走的时候,我如何保证在深度为2的运算空间里,我可以遍历除了已经遍历过的元素(这里就是2)之外的所有元素?
循环登场
我设定循环为遍历1~n的元素,那么我就可以在每个深度的运算空间里遍历所有的元素。这里是所有的元素,当然也包括了已经遍历过的元素(这里就是2)。那么如何剔除遍历过的元素呢?
伟大的哨兵登场了
当我们每遍历一个元素,就把这个元素标记为已用,那么在下一个深度空间里,通过哨兵的报告,我们就可以避免再次遍历已经遍历过的元素了。这就是标记点A的作用。至此,问题X不解决了吗?
那么,还有一个问题:标记点B是做什么的?为什么在回溯时要将当前元素又标记为未用呢?
继续探究,我们来举个栗子:

假如没有标记点B:
当我们以1为起点,找到12和13后,回溯到深度为1的运算空间,然后大问题来了,哨兵报告说:“已经没有可用元素了!”。
这明显不对啊,这时候标记点B的作用就体现出来了。
我们来看看有标记点B的情况:
找到12和13后,我们又回溯到了深度为1的运算空间,这时候,由于标记点B的存在,1号和2号元素又被标记为未用哨兵报告你说:“2号元素可用!”,然后我们就可以以2为起点,继续查找新的排列方案。
总结下哨兵、循环在排列问题中的作用
满循环:即指遍历所有元素,保证在每个深度的运算空间空间里可以遍历所有的元素。
哨兵:标记点A,保证在查找单个排列时,不会使用当前排列已经使用过的元素;
标记点B,保证在查找另一个排列方案时,可以使用已经找到的排列时用过的元素。
这里说的有点复杂,我们再举个栗子解释一下:
标记点A:当我从1开始,递归进入深度为2的运算空间时,我不能再使用1号元素。12(或者13)就是当前排列,1号元素就是当前排列已经使用过的元素。
**标记点B:**当我找到12和13的时候(这时候12和13就是已经找到的排列,2就是已经找的排列用过的元素),我仍然可以以2为起点再次查找新的排列方案。
问题二:分析组合
之前我们说了。组合和排列的代码块在循环和哨兵的使用方面存在差异,
对比排列,我们发现组合没有使用哨兵,并且不是满循环。显而易见,组合的代码使用的循环,他的起点就是当前dfs的深度(暂且称这种循环为变起点式循环)。
我们来探究下为什么组合不使用哨兵,且使用的是变起点式循环
又到了举栗子的时间(仍然使用上面那幅图):

假如我们使用的是哨兵+满循环组合:
当我们从2开始遍历,,那么我们就会得到21和23,(从1遍历时得到了12)那么21和12显然是重复的组合。
那如何避免这种组合重复的问题呢?
我们先来探究为什么会出现21这种重复的组合。显而易见,是因为我们遍历了起点2之前的元素1,如果我们不遍历起点之前的元素,不就不会出现重复组合了吗?如何做到呢?
变起点式循环闪亮登场
通过变起点循环,我们很容易就保证了绝对不会遍历起点之前的元素。
我们再来探究下为什么组合代码不使用哨兵
变起点式循环只遍历数表中起点之后余下的数,所以标记点A和标记点B所解决的问题在这里都不会出现,自然也就不需要哨兵了。(不再赘述)。
