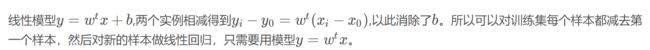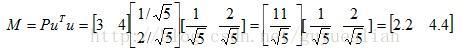《机器学习》课后习题——第三章 线性模型
文章目录
- 3.1
- 3.3
- 3.4
- 3.5
- 3.7
- 3.8
- 3.9
3.1
试分析在什么情况下,在以下式子中不比考虑偏置项b。
3.3
编程实现对率回归,并给出西瓜数据集3.0α上的结果
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
def func(item):
if item == '是':
return 1
else:
return 0
# 似然函数
def l_beta(x_hat, y, beta):
beta = beta.reshape(-1, 1)
y = y.reshape(-1, 1)
return np.sum(-y * np.dot(x_hat, beta) + np.log(1 + np.exp(np.dot(x_hat, beta))))
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def gradient(x_hat, y, beta):
y = y.reshape(-1, 1) # 行向量转为列向量
beta = beta.reshape(-1, 1) # 行向量转为列向量
p1 = sigmoid(np.dot(x_hat, beta)) # 列向量
return -np.sum(x_hat * (y - p1), axis=0) # 行向量
# 梯度下降法
def update_parameters_gradDesc(beta, x_hat, y, learning_rate, num_iterations):
for i in range(num_iterations):
grad = gradient(x_hat, y, beta)
beta -= learning_rate * grad
if i % 50 == 0:
print('{}th iteration, likelihood function is {}\n'.format(i, l_beta(x_hat, y, beta)))
return beta
def hessian(x_hat, y, beta):
y = y.reshape(-1, 1) # 行向量转为列向量
beta = beta.reshape(-1, 1) # 行向量转为列向量
p1 = sigmoid(np.dot(x_hat, beta)) # 列向量
m = x_hat.shape[0]
P = np.eye(m) * p1 * (1 - p1)
return np.dot(np.dot(x_hat.T, P), x_hat) # 矩阵
def update_parameters_newton(beta, x_hat, y, num_iterations):
for i in range(num_iterations):
grad = gradient(x_hat, y, beta)
hess = hessian(x_hat, y, beta)
beta -= np.dot(np.linalg.inv(hess), grad)
if i % 50 == 0:
print('{}th iteration, likelihood function is {}'.format(i, l_beta(x_hat, y, beta)))
return beta
def init_beta(n):
return np.random.randn(n+1)
def logistic_regression(x_hat, y, method, learning_rate, num_iterations):
'''
w: 权重向量(行向量)
x: 自变量(一行为一个示例)
b: 截距项(常数)
return:
beta = [w, b]
'''
beta = init_beta(x.shape[1])
if method == 'gradDesc':
return update_parameters_gradDesc(beta, x_hat, y, learning_rate, num_iterations)
elif method == 'newton':
return update_parameters_newton(beta, x_hat, y, num_iterations)
data = pd.read_csv('watermelon3_0_Ch.csv')
data = data.iloc[:, 7:]
data['好瓜'] = data['好瓜'].map(func)
x = data.iloc[:, :2].values
y = data.iloc[:, -1].values
x_hat = np.append(x, np.ones((x.shape[0], 1)), axis=1)
beta = logistic_regression(x_hat, y, method='newton', learning_rate=0.3, num_iterations=1000)
# 可视化模型结果
beta = beta.reshape(-1, 1)
x1 = np.arange(len(y))
y1 = sigmoid(np.dot(x_hat, beta))
lr = linear_model.LogisticRegression(solver='lbfgs', C=1000) # 注意sklearn的逻辑回归中,C越大表示正则化程度越低。
lr.fit(x, y)
lr_beta = np.c_[lr.coef_, lr.intercept_].T
y2 = sigmoid(np.dot(x_hat, lr_beta))
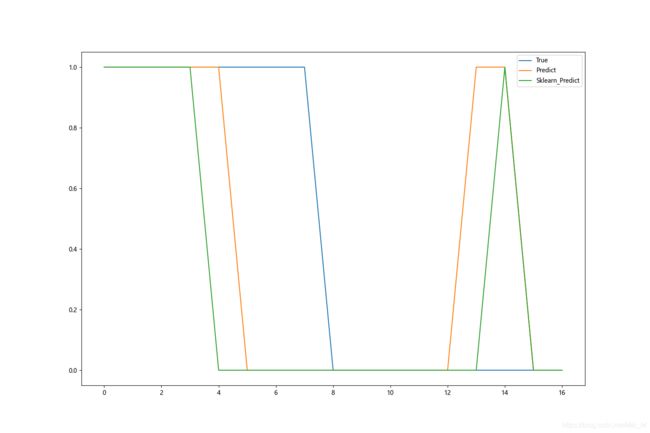
plt.plot(x1, y1, 'r-', x1, y2, 'g--', x1, y, 'b-')
plt.legend(['predict', 'sklearn_predict', 'true'])
plt.show()
3.4
选择两个 UCI 数据集,比较 10 折交叉验证法和留一法所估计出的对率回归的错误率。
import numpy as np
from sklearn import linear_model
from sklearn.model_selection import LeaveOneOut, KFold
# 数据地址:https://archive.ics.uci.edu/ml/datasets/Blood+Transfusion+Service+Center
data = np.loadtxt('Transfusion.txt', skiprows=3, delimiter=',').astype(int)
X = data[:, :4]
y = data[:, 4]
n = X.shape[0]
# normalization
X = (X - np.mean(X, axis=0)) / np.std(X, axis=0)
# 10折交叉验证法
kf = KFold(n_splits=10, shuffle=True)
accuracy = 0
for train_index, test_index in kf.split(X):
lr = linear_model.LogisticRegression(C=2)
X_train, X_test = X[train_index], X[test_index]
y_train, y_test = y[train_index], y[test_index]
lr.fit(X_train, y_train)
accuracy += lr.score(X_test, y_test)
print('10折交叉验证法准确率:{:.2%}'.format(accuracy / 10))
# 留一法
loo = LeaveOneOut()
accuracy = 0
loo = LeaveOneOut()
for train_index, test_index in loo.split(X):
lr = linear_model.LogisticRegression(C=2)
X_train, X_test = X[train_index], X[test_index]
y_train, y_test = y[train_index], y[test_index]
lr.fit(X_train, y_train)
accuracy += lr.score(X_test, y_test)
print('留一法准确率:{:.2%}'.format(accuracy / n))
3.5
编程实现线性判别分析,并给出西瓜数据集 3.0α 上的结果.
https://www.cnblogs.com/pinard/p/6244265.html
https://blog.csdn.net/guyuealian/article/details/53954005
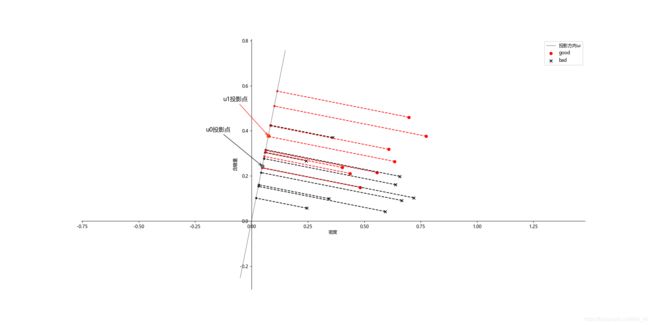
用到的知识为点在某方向上的投影坐标,这里使用向量投影法,将问题转为向量 w 2 w_2 w2在向量 w 1 w_1 w1方向的投影
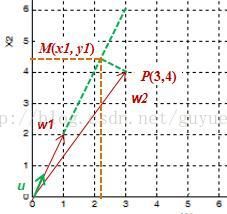
思路:用 u u u表示 w 1 w_1 w1方向的单位向量(即上图中的绿色剪头 u u u,也是 w 1 w_1 w1归一化后的单位向量),向量 w 2 w_2 w2在向量 w 1 w_1 w1方向的投影坐标,即为向量 O M OM OM,由几何知识得:
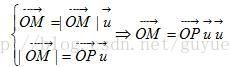
上式中, u u u是向量 w 1 w_1 w1的单位向量,即:
![]()
利用上式,可以得到向量 w 2 w_2 w2在向量 w 1 w_1 w1方向的投影坐标,即点 P = ( 3 , 4 ) P=(3,4) P=(3,4)在直线 w 1 w_1 w1的投影坐标为:
# coding:utf-8
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
class LDA():
def fit(self, X, y):
pos = y == 1
neg = y == 0
X0 = X[neg]
X1 = X[pos]
u0 = np.mean(X0, axis=0, keepdims=True) # (1, n)
u1 = np.mean(X1, axis=0, keepdims=True)
Sw = np.dot((X0 - u0).T, X0 - u0) + np.dot((X1 - u1).T, X1 - u1)
w = np.dot(np.linalg.inv(Sw), (u0 - u1).T).reshape(1, -1) # (1, n)
fig, ax = plt.subplots(figsize=(20, 10))
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.spines['left'].set_position(('data', 0))
ax.spines['bottom'].set_position(('data', 0))
plt.scatter(X1[:, 0], X1[:, 1], c='r', marker='o', label='good')
plt.scatter(X0[:, 0], X0[:, 1], c='k', marker='x', label='bad')
plt.xlabel('密度', labelpad=1)
plt.ylabel('含糖量')
x_tmp = np.linspace(-0.05, 0.15)
y_tmp = x_tmp * w[0, 1] / w[0, 0]
plt.plot(x_tmp, y_tmp, '#808080', linewidth=1, label='投影方向ω')
wu = w / np.linalg.norm(w) # 转化为单位向量
# 样本点投影(参考:https://blog.csdn.net/guyuealian/article/details/53954005)
X0_project = np.dot(X0, np.dot(wu.T, wu))
plt.scatter(X0_project[:, 0], X0_project[:, 1], c='k', s=15)
for i in range(X0.shape[0]):
plt.plot([X0[i, 0], X0_project[i, 0]], [X0[i, 1], X0_project[i, 1]], 'k--')
X1_project = np.dot(X1, np.dot(wu.T, wu))
plt.scatter(X1_project[:, 0], X1_project[:, 1], c='r', s=15)
for i in range(X1.shape[0]):
plt.plot([X1[i, 0], X1_project[i, 0]], [X1[i, 1], X1_project[i, 1]], 'r--')
# 中心点投影
u0_project = np.dot(u0, np.dot(wu.T, wu))
plt.scatter(u0_project[:, 0], u0_project[:, 1], c='#696969', s=60)
u1_project = np.dot(u1, np.dot(wu.T, wu))
plt.scatter(u1_project[:, 0], u1_project[:, 1], c='#FF4500', s=60)
ax.annotate(
'u0投影点',
xy=(u0_project[:, 0], u0_project[:, 1]),
xytext=(u0_project[:, 0] - 0.25, u0_project[:, 1] + 0.16),
size=13,
va='center',
ha='left',
arrowprops=dict(
arrowstyle='->',
color='k'
)
)
ax.annotate(
'u1投影点',
xy=(u1_project[:, 0], u1_project[:, 1]),
xytext=(u1_project[:, 0] - 0.2, u1_project[:, 1] + 0.16),
size=13,
va='center',
ha='left',
arrowprops=dict(
arrowstyle='->',
color='r'
)
)
plt.legend(loc='upper right')
plt.axis("equal") # 两坐标轴的单位刻度长度保存一致
plt.savefig('3.5.png')
plt.show()
self.w = w
self.u0 = u0
self.u1 = u1
def predict(self, X):
project = np.dot(X, self.w.T)
w_u0 = np.dot(self.w, self.u0.T)
w_u1 = np.dot(self.w, self.u1.T)
# 投影点到 w_u1的距离比到w_u0的距离近,即归为1的一类点
return (np.abs(project - w_u1) < np.abs(project - w_u0)).astype(int)
data = pd.read_csv('../3.3/watermelon3_0_Ch.csv').values
X = data[:, 7:9].astype(float)
y = data[:, 9]
y[y == '是'] = 1
y[y == '否'] = 0
y = y.astype(int)
lda = LDA()
lda.fit(X, y)
y_predict = lda.predict(X).flatten()
clf = LinearDiscriminantAnalysis()
clf.fit(X, y)
y_clf_predict = clf.predict(X)
plt.figure(figsize=(15, 10))
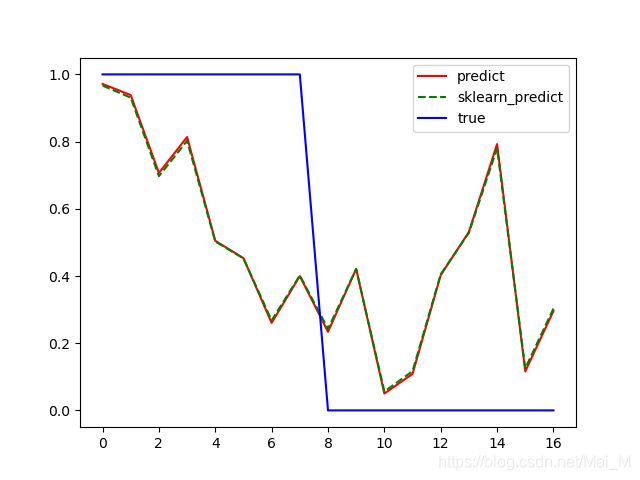
plt.plot(np.arange(X.shape[0]), y, label='True')
plt.plot(np.arange(X.shape[0]), y_predict, label='Predict')
plt.plot(np.arange(X.shape[0]), y_clf_predict, label='Sklearn_Predict')
plt.legend()
plt.savefig('predict.png')
plt.show()
3.7
令码长为 9,类别数为 4,试给出海明距离意义下理论最优的 ECOC二元码并证明之。
答:
原书对很多地方解释没有解释清楚,把原论文看了一下《Solving Multiclass Learning Problems via Error-Correcting Output Codes》。
先把几个涉及到的理论解释一下。
首先原书中提到:
对同等长度的编码,理论上来说,任意两个类别之间的编码距离越远,则纠错能力越强。因此,在码长较小时可根据这个原则计算出理论最优编码。
其实这一点在论文中也提到
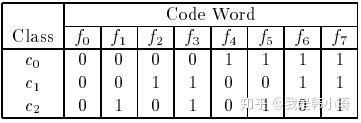
“假设任意两个类别之间最小的海明距离为 d d d ,那么此纠错输出码最少能矫正 [ d − 1 2 ] \big [\frac{d-1}{2} \big ] [2d−1] 位的错误。
拿上图论文中的例子解释一下,上图中,所有类别之间的海明距离都为4,假设一个样本正确的类别为 c 1 c_1 c1 ,那么codeword应该为 ‘0 0 1 1 0 0 1 1’,若此时有一个分类器输出错误,变成‘0 0 0 1 0 0 1 1’,那么此时距离最近的仍然为 c 1 c_1 c1 ,若有两个分类输出错误如‘0 0 0 0 0 0 1 1’,此时与 c 1 , c 2 c_1, c_2 c1,c2 的海明距离都为2,无法正确分类。即任意一个分类器将样本分类错误,最终结果依然正确,但如果有两个以上的分类器错误,结果就不一定正确了。这是 [ d − 1 2 ] \big [\frac{d-1}{2} \big ] [2d−1] 的由来。
此外,原论文中提到,一个好的纠错输出码应该满足两个条件:
- 行分离。任意两个类别之间的codeword距离应该足够大。
- 列分离。任意两个分类器 f i , f j f_i, f_j fi,fj 的输出应相互独立,无关联。这一点可以通过使分类器 f i f_i fi 编码与其他分类编码的海明距离足够大实现,且与其他分类编码的反码的海明距离也足够大(有点绕。)。
第一点其实就是原书提到的,已经解释过了,说说第二点:
如果两个分类器的编码类似或者完全一致,很多算法(比如C4.5)会有相同或者类似的错误分类,如果这种同时发生的错误过多,会导致纠错输出码失效。(翻译原论文)
个人理解就是:若增加两个类似的编码,那么当误分类时,就从原来的1变成3,导致与真实类别的codeword海明距离增长。极端情况,假设增加两个相同的编码,此时任意两个类别之间最小的海明距离不会变化,依然为 d d d ,而纠错输出码输出的codeword与真实类别的codeword的海明距离激增(从1变成3)。所以如果有过多同时发出的错误分类,会导致纠错输出码失效。
另外,两个分类器的编码也不应该互为反码,因为很多算法(比如C4.5,逻辑回归)对待0-1分类其实是对称的,即将0-1类互换,最终训练出的模型是一样的。也就是说两个编码互为补码的分类器是会同时犯错的。同样也会导致纠错输出码失效。
当然当类别较少时,很难满足上面这些条件。如上图中,一共有三类,那么只有 2 3 = 8 2^3=8 23=8 种可能的分类器编码( f 0 ∼ f 7 f_0 \sim f_7 f0∼f7 ),其中后四种( f 4 ∼ f 7 f_4 \sim f_7 f4∼f7 )是前四种的反码,都应去除,再去掉全为0的 f 0 f_0 f0,就只剩下三种编码选择了,所以很难满足上述的条件。事实上,对于 k k k 种类别的分类,再去除反码和全是0或者1的编码后,就剩下 2 k − 1 − 1 2^{k-1}-1 2k−1−1 种可行的编码。
回到题目上,在类别为4时,其可行的编码有7种,按照上述方法有:

当码长为9时,那么 f 6 f_6 f6 之后加任意两个编码,即为最优编码,因为此时再加任意的编码都是先有编码的反码,此时,类别之间最小的海明距离都为4,不会再增加。
3.8
ECOC 编码能起到理想纠错作用的重要条件是:在每一位编码上出错的概率相当且独立。试析多分类任务经 ECOC 编码后产生的二类分类器满足该条件的可能性及由此产生的影响。
答:
条件分解为两个:一是出错的概率相当,二是出错的可能性相互独立。
先看第一个,其实就是每一位上的分类器的泛化误差相同,要满足这个条件其实取决于样本之间的区分难度,若两个类别本身就十分相似,即越难区分,训练出的分类器出错的概率越大,原书p66也提到:
将多个类拆解为两个"类别子集“,所形成的两个类别子集的区分难度往往不同,即其导致的二分类问题的难度不同。
所以每个编码拆解后类别之间的差异越相同(区分难度相当),则满足此条件的可能性越大。在实际中其实很难满足。
第二个,相互独立。在3.7中也提到过,原论文中也提出一个好的纠错输出码应该满足的其中一个条件就是各个位上分类器相互独立,当类别越多时,满足这个条件的可能性越大,在3.7中也解释了当类别较少时,很难满足这个条件。
至于产生的影响。西瓜书上也提到:
一个理论纠错牲质很好、但导致的二分类问题较难的编码,与另一个理论纠错性质差一些、但导致的二分类问题较简单的编码,最终产生的模型性能孰强孰弱很难说。
3.9
使用 OvR 和 MvM 将多分类任务分解为二分类任务求解时,试述为何无需专门针对类别不平衡性进行处理。
答:
对 OvR 、 MvM 来说,由于对每个类进行了相同的处理,其拆解出的二分类任务中类别不平衡的影响会相互抵消,因此通常不需专门处理.