与Scheme共舞
发表在《程序猿》2007年7月刊上。不log上写帖子不用考虑版面限制，所以这里的帖子比发表的啰嗦点。赵健平编辑，Jacky，和刘未鹏都给了我非常多帮助，在这里一并谢了。免费的Scheme实现非常多。我用的是PLT Scheme，能够到这里下载。PLT Scheme的IDE（Dr. Scheme）支持Emacs的键盘绑定，用emacs的老大们应该喜欢。Dr.Scheme内置中文支持：
以下是正文：
不能影响你思考方式的编程语言不值得学习 – Alan Perlis [1]
不少朋友问，为什么要学Scheme这样无数括号包裹的语言。答案非常easy：帮你理解计算的本质，成为更优秀的程序猿。Scheme好比大还丹。没人拿药丸儿当板砖拍人，但服了它却能指望十步杀一人，千里不留行。
1975年问世的Scheme是Lisp方言。所以最好还是从Lisp谈起。Lisp是一门传奇语言，诞生50年，仍然影响深远。程序猿们似乎不断“发现”Lisp里简单却深刻，浅显但强大的特性，并应用到不同地方，取得非凡成就。比方近期热火的Ruby、Python、以及JavaScript中很多为人称道的功能源于Lisp。或许John K. Foderaro的比喻和总结最能说明Lisp的价值：Lisp好比变色龙，高度适应环境的改变，由于
它是一门能够编程的编程语言。我们不仅能够用Lisp编程，还能够对Lisp编程
[2]。Lisp内置的抽象方法让Lisp程序猿们身段灵活，长袖善舞。每当新的编程范式出现，Lisp程序猿们总能高速实现相关功能，甚至做出进一步改进。比方Smalltalk展示面向对象编程的潜力后，MIT媒体实验室的Cannon Howard便在1982年推出Flavors，一个功能丰富的面向对象扩展。Cannon的扩展不仅实现了 当时流行的面向对象功能，还首创了多继承，多重分派，以及被Ruby程序猿狂赞的mixin
[3]。尔后在Xerox PARC的
Gregor Kiczales又在集大成的Common Lisp面向对象扩展 — CLOS — 里增加面向方面（AOP）的编程方法
[4]。Gregor也是面向方面编程的发起人和AspectJ的作者。熟悉Java的老大应该对他不陌生。事实上CLOS支持的method combination已经支持AOP里的before/after/around处理。AOP和CLOS出于同一人之手，应该不是巧合。顺便说一句，Gregor1993年的名作
The Art of Meta Object Protocol也值得细读。
传奇语言自有传奇历史。1958年，John McCarthy从达特茅斯搬到MIT。当时人工智能的还有一奠基人Marvin Minsky也在那里。牛人相见，好比利刃相击，火花耀眼。著名的MIT人工智能计划上马
[5]。研究AI的过程中，McCarthy须要一门编程语言描写叙述他的理论模型。当时人见人爱的图灵机仅仅有一套笨拙的语言，不适合干净利落地表达复杂的递归函数，所以McCarthy在丘齐的lambda算子基础上设计了Lisp。早期的Lisp是纯理论工具，用来帮助项目组进行程序的推导和证明。实在须要用机器验证理论了，研究组的老大们就手工把Lisp程序翻译成IBM 740的汇编代码，再上载到IBM 740上执行。人肉编译器们甚至热衷于编译各式Lisp程序，认为跟解智力题一样好玩儿。他们还证明了能够用Lisp写出一个通用函数eval(), 用来解释执行Lisp的表达式
[6]。但他们光顾赞叹eval()和元图灵机一样彪悍，且比图灵机构造出元图灵机的代码美妙，并没想到eval就是一个通用的Lisp解释器。幸好有天McCarthy的学生S.R. Russell灵机闪现，连夜用IBM704的机器语言实现eval()。于是世界上第一个Lisp解释器横空出世，绿色低功耗无污染的人肉编译才渐渐失传。那时真是计算机科学研究的黄金时代啊，人们能够一夜之间改变世界，比居委会大妈在股市一夜暴富还来得轻快。顺便提一下，我们习以为常的条件推断语句，也是McCarthy在Lisp里发明的。而为了让函数应用没有副作用和实现函数闭包，McCarthy的研究小组又顺便发明了垃圾收集。1975年，同是MIT的Gerald Jay Sussman和Guy Steele为了研究Carl Hewitt的面向对象模型，用Lisp编写了一个玩具语言。这个玩具语言简化了当时流行的Lisp语法，引入了词法定界（又叫静态范围）和Continuation两大革新。Sussman和Steele给这门语言取名Schemer，希望它发展成像AI里著名系统Planner一样的有力工具。可惜当时MIT用的操作系统ITS仅仅同意最长6个字节的文件名称。Sussman和Steele不得不把Schemer的最后一个字幕’r’去掉。Scheme问世便显露峥嵘：Sussman和Steele非常快发现Scheme的函数和Hewitt模型里的演员（也就是我们如今所谓的对象）没有本质差别，连句法都基本一致
[7]。其实，Sussman在教材《计算机程序设计与解释》的第二章用短短几十行代码展示了一套面向对象系统。
Scheme是极度简化的语言。他的规范文档只是47页
[8]。相比Lisp还有一大分支Common Lisp规范的上千页文档或者Java规范的500来页文档，可见Scheme的短小精悍。只是，我们仍然可用Scheme写出优雅犀利的程序。Scheme规范R
5RS开篇道出了Scheme的设计宗旨：设计编程语言时不应堆砌功能，而应去掉让多余功能显得必要的弱点和限制。Smalltalk的发明人Alan Kay在一次訪谈录中提到，Lisp是编程语言中的麦克斯韦方程组
[9]。这句评价用到Scheme上更为合适。Scheme甚至让我们写出用其它语言无法轻易写出的程序。Sussman和Steele用Scheme探索不同的编程模型时时，往往一周做出十来种不同的解释器，能够旁证Scheme的简洁和灵活。在解释是什么造就了Scheme的精练与生猛之前，我们先介绍一下Scheme的基本元素：
- Scheme的语法结构 大道至简。Scheme的结构就两种：原子和表达式。原子是诸如数，字符串，布尔值，变量，空表这类简单数据。对非变量的原子求值，得到原子自身。对变量求值，得到变量绑定的值。比方说，对1求值得到1，但假设对变量A求值，而A和字符串”A”绑定，则得到字符串“A”。表达式的形式也仅仅有一种：列表。一对括号包括起来的就是列表。表里的元素用空格分开。列表能够嵌套。这种表达式在Lisp里叫做S-表达式，意思是符号表达式。以下是一些样例：
- ( )： 一个空表
- (1 2 3 4 5)：一个包括五个整数的表
- (1 “a” 1.5 #t #f)：一个列表，依次包括整数、字符串、浮点数、为真的布尔值、和为假的布尔值
- (1 (2 3) )：一个嵌套列表，第二个元素(2 3)也是一个表
- (+ 2 3)：一个表达式，表示把2和3相加。Scheme里全部的操作符都是前缀操作符，即操作符在前，操作数据在后。比方说4 * (2 + 3)在Scheme里表达为(* 4 (+ 2 3))。非常多人看无论这样的方式。只是细致思考一下，能够看出前置操作符让不论什么操作符都是多维的。比方说。假设我们要把1到5的整数相加，用中缀操作符，就得写成 1 + 2 + 3 + 4 + 5。同一个加好反复了4次。而用前缀操作符，仅仅须要写一次：(+ 1 2 3 4 5)。推而广之，假设我们要把一列数加起来，就得用到循环。而在Scheme里则不须要。并且前缀操作符去掉了优先级问题：我们能够通过括号来推断每一个表达式的优先级。
- (lambda (x y) (sqrt (* x y))。这个表达式定义了一个匿名函数，计算并返回參数x和y的几何平均值。当一个表达式以lambda开头的时后，我们就知道要定义一个函数了。
- (define zero 0)：这个表达式把一个变量zero绑定到一个整数0。在Scheme里，全部变量本质上都是指针。指针本身没有类型，他们指向的值才有类型。换句话说，Scheme是动态类型语言。
- (car ‘(1 2 3 4))：这个表达式调用函数car。函数car接收一个列表參数，并返回这个參数的第一个值，也就是1。注意样例里的參数(1 2 3 4)前有一单引號。这是由于Scheme总是把一个普通列表当作表达式计算。加上单引號相当于告诉Scheme，不要对(1 2 3 4)估值，把它当成数据对待。假设不加这个单引號，Scheme会运行(1 2 3 4)。运行的规则是把该列表的第一个元素当成函数来调用。而第一个元素是1，不是函数，Scheme会抛出错误。
- (cdr ‘(1 2 3 4))： 这个表达式调用函数cdr（读作kuder）。函数cdr也是把一个列表作为參数，并返回这个列表除去第一个元素后的子表。所以对(cdr ‘(1 2 3 4))求值，就得到(2 3 4)。
- Scheme的数据类型 Scheme提供了各种通用的数据类型：整数，浮点数，复数，有理数，字符串，布尔变量，散列，数组，矢量，点对，和列表。值得一提的是点对(pair)和列表。这俩哥们儿是Scheme编程的基石。还是用样例说明比較好：
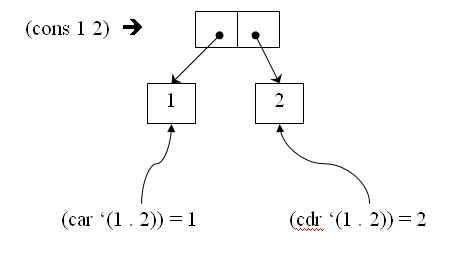
- (1 . 2)是一个点对。一个点对包括两个指针，每一个指针指向一个值。我们用函数cons构造点对。比方说(cons 1 2)就构造出点对(1 . 2)。由于点对总是又函数cons构造，点对又叫做cons cell。点对左边的值能够用函数car取出来，右边的值能够由函数cdr取出来。以下是图示：
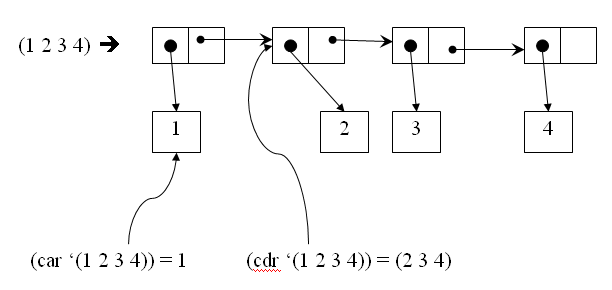
- 假设一个点对右边不是一个值，而是一个指针，指向另外一个列表，我们就得到了列表。比方以下的图表示列表(1 2 3 4)，实际上由点对构成：(1 . (2 . (3 . 4. ‘())。能够看出，列表本质是单向链表。
- (1 . 2)是一个点对。一个点对包括两个指针，每一个指针指向一个值。我们用函数cons构造点对。比方说(cons 1 2)就构造出点对(1 . 2)。由于点对总是又函数cons构造，点对又叫做cons cell。点对左边的值能够用函数car取出来，右边的值能够由函数cdr取出来。以下是图示：
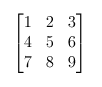
- 不要小看了列表。这个看似简单的数据类型的具有丰富的表达能力。比方我们能够把以下2x3的矩阵表达为((1 2 3) (4 5 6) (7 8 9)):
而以下的树也能够用列表直观表达：(A B C (D (F H) G) E)。也就是说，每一个列表表示一个树或子树。列表的第一个元素是根。 
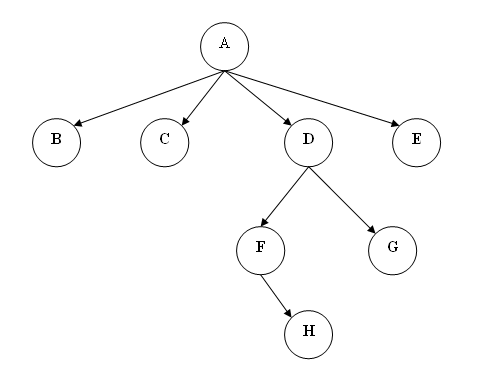
- 函数 函数在Scheme里是一等公民。定义的函数能够被当成数据传递或返回。有三种定义函数的方法：
- 用lambda操作符定义一个匿名函数。比方(lambda (x) (* 2 x))定义了一个函数，返回參数x的倍数。操作符lambda后第一个子列表是參数列表，而第二个子列表是函数定义。这和JavaScript里的匿名函数没有本质差别： function(x){return 2 * x;}
- 用define绑定函数名：(define 1+ (lambda (x) (+ 1 x)))。这个样例定义了递加函数，并把它绑定到函数名1+上。。Scheme对函数名没有限制。其实，Scheme对全部函数名一视同仁。规范里定义的函数没有特殊地位，我们全然能够用自己的函数定义代替。这相当于以下的JavaScript语法： var increment = function(x){return x + 1;}。
- Scheme还提供了一条捷径，省去lambda。以下的样例用大小比較定义相等函数。函数名是same? 而參数就是后面的x和y。 (define (same? x y) (not (or (> x y) (< x y))) 这种定义方式和JavaScript里的经常使用函数定义方式一致。呵呵，能够看出JavaScript从哪里获得灵感的了吧？以下是等价的JavaScript定义： function isSame(x, y){ return !((x > y) || (x < y)); }
非常多老大看不惯括号。事实上Lisp刚诞生时，John McCarthy设计了叫M-表达式的语法，与C/C++的语法相似。比方S-表达式(cdr ‘(1 2 3)用M-表达式就写成cdr[1, 2, 3]。可是Lisp的程序猿们纷纷放弃了M-表达式，选择直接使用S-表达式。S-表达式的实质是用抽象句法树(AST)表达程序，直接省去了解析这道工序。比方说，a+b*c解析成AST后，和下图一致。而该AST的表示不正好是(+ a (* b c))么？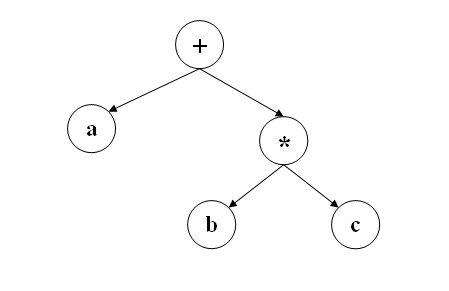 
更重要的是，既然程序就是句法树，程序和数据的表示就统一了。程序即数据，数据即程序。我们遍历列表改动数据。同理，我们也能够遍列类表改动程序。正是这种统一处理带给Scheme无与伦比的威力：不管是编译时还是执行时，我们都能够改动，注入，载入，或者生成新的程序 — 这些无非是在AST里改动或加入节点而已。我们甚至能够改动或加入新的句法。
明了这些基本概念，就能够领略Scheme的妙处了。Scheme最为人称道的功能之中的一个是它的函数编程能力。所谓函数编程，是指用一系列函数应用实现程序。每一个函数接受參数，计算后返回结果。计算过程中没有副作用，不改变不论什么变量的状态。同一时候，函数本身是一等公民，能够作为数据传入另外的函数，也能够作为结果被其他函数返回。这种优点是什么嗫？一言以蔽之：黏合
[10]。我们用简单的函数描写叙述系统的不同功能。每一个函数高内聚，低耦合（參数进，结果出。没有副作用。想低内聚高耦合都不easy）。Scheme提供很多方便的工具把这些函数黏合起来。这种高度支持模块化编程的能力绝对让人惊叹。多说无益。看样例。
§ 定义一个函数sum-of-squares计算一列数的平方和。比方说(sum-of-squares ‘(1 2 3 4))返回的结果是30。以下是Scheme的代码。
測试结果：
假设哪位老大不认为这个函数定义优雅的话，最好还是试试用命令编程的方式重写。比方说用C，用Java，或者用Pascal。 解剖一下上面的函数定义：
測试结果：
假设哪位老大不认为这个函数定义优雅的话，最好还是试试用命令编程的方式重写。比方说用C，用Java，或者用Pascal。 解剖一下上面的函数定义：
o 第一行 (define (sum-of-squares numbers) 表示定义一个函数。函数名为sum-of-squares，而函数接受一个參数。
o 第二行是函数的定义。计算顺序是：先调用函数map，在把函数+(Scheme里一切都是函数。相加也是函数)应用到得到的结果上。
o 函数map是一个高端函数。所谓高端，是指这个函数能够接受或返回函数。函数map接受两个或多个參数。第一个參数必须是函数，而其他參数则必须是列表。函数map会同步遍历全部的列表，并把第一个參数应用到遍历时遇上的每一个元素，并把结果放到一个新表里。在上面的样例里，函数map的第一个參数是个匿名函数：(lambda (x) (* x x))。这个匿名函数接受一个參数，x，并返回x的平方。我们来看看(map (lambda (x) (* x x)) ‘(1 2 3))这个样例：map从遍历列表(1 2 3)開始，一次取出1， 2， 最后3。对每一个取出的元素，应用第一个參数定义的函数。比方取出2时，应用(lambda (x) (* x x))就得到(* 2 2)，结果为4。所以最后的结果就是(1 4 9)。
o 顾名思义，函数apply负责应用函数。它接受两个參数。第一个參数是函数，第二个參数必须是列表。列表相应被应用函数接受的參数列表。比方说，(apply + ‘(1 2 3 4))就是把相加应用到參数(1 2 3 4)上，和(+ 1 2 3 4)等价。这里也显出了用前缀操作符的优点：每一个函数都能够接受随意多个參数。再举个样例：(apply car ‘((a b c d)))等价与(car ‘(a b c d))，得到的结果是a。注意哈，函数apply的最后一个參数在传入第一个參数代表的函数时，最外面的一层括号被剥去。所以我们要把列表(a b c d)传给函数car，就得写成((a b c d))。
我们在编程里往往须要处理一系列数据，比方说把对一列整数求和，找出一个文件里每行里的电话号码，把一列数据转换成另外一列数据。。。假设在普通的命令式语言里，我们会用各式循环来处理。问题是，事实上这些循环极其类似：遍历列表中每一个数据，对每一个数据做出一定的处理。遍历本身都是一样的，不同的仅仅是处理数据的方式。而Scheme正是通过函数map抽象出了遍历的普遍形式。处理数据的详细样例被抽象成了函数。最后通过高端函数这个“黏合剂”，让我们享受到如此妖娆的代码。熟悉
Google MapReduce，
Apache Hadoop，或者
Ruby Starfish的老大们又猜对了：MapReduce的灵感来自函数编程里经常使用的map和reduce函数。MapReduce本身是用C++写的。这多少能够说明，哪怕我们仅仅用主流编程语言，学习其他编程范式也能增长我们的功力。
§ 再来一个样例：求出两个矢量的点乘。比方说[a, b, c, d] x [e, f, g, h]就等于a*e + b*f + c*g + d*h。假设我们定义函数dot-product, 那么(dot-product ‘(1 2 3 4) ‘(5 6 7 8))就等于1x5+2x6+3x7+4x8 = 70：
这次函数map同步遍历两个列表，所以定义的匿名函数也接受两个參数。Scheme里的map函数能够同一时候遍历随意多个列表。Scheme里的函数调用都是S-表达式列表。所以遍历一个列表也好，多个列表也好，都是处理一个S-表达式的尾巴，没有本质差别。哪位老大有兴趣，最好还是了解了Scheme宏的使用方法（后面会讨论）后，实现自己的map函数。
这次函数map同步遍历两个列表，所以定义的匿名函数也接受两个參数。Scheme里的map函数能够同一时候遍历随意多个列表。Scheme里的函数调用都是S-表达式列表。所以遍历一个列表也好，多个列表也好，都是处理一个S-表达式的尾巴，没有本质差别。哪位老大有兴趣，最好还是了解了Scheme宏的使用方法（后面会讨论）后，实现自己的map函数。
§ 还不够奇妙？那写个矩阵转置函数怎么样? 所谓矩阵转置，是说把M x N的矩阵的行和列兑换，得到NxM的矩阵。比方以下的样例。给出矩阵A， A的转置矩阵A
T就等于矩阵B：
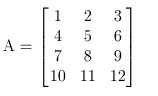
假设我们定义了函数transpose，那么用上面的样例，调用函数(transpose ‘((1 2 3) (4 5 6) (7 8 9) (10 11 12))就应该得到((1 4 7 10) (2 5 8 11) (3 6 9 12))。实现这个函数得多少代码呢？请看—
一行代码，四个函数。还有比这更干净利落的么？我们详细分析一下：
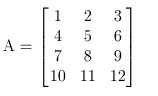
假设我们定义了函数transpose，那么用上面的样例，调用函数(transpose ‘((1 2 3) (4 5 6) (7 8 9) (10 11 12))就应该得到((1 4 7 10) (2 5 8 11) (3 6 9 12))。实现这个函数得多少代码呢？请看—
一行代码，四个函数。还有比这更干净利落的么？我们详细分析一下：
o 和前面描写叙述的一样，函数应用从里到外进行。所以调用(transpose matrix)时，(cons list matrix)先被运行，然后函数map被应用到运行的结果上。
o list是Scheme提供的一个函数。它接受随意參数，并把全部參数一次放到一个列表里，然后返回这个列表。比方说(list ‘a)返回(a)，(list 1 2 3 4)返回(1 2 3 4)。注意这里我们不用写成(list ‘1 ‘2 ‘3 ‘4)，为Scheme里，对数字计算得到数字本身。最后一个样例：(list ‘(1 2) ‘(3 4) ‘(5 6))得到((1 2) (3 4) (5 6))。
o 函数cons前面提到过。它接受两个參数，返回这两个參数合成的点对。比方说(cons ‘a ‘b)就得到(a . b)，而(cons 1 ‘(2 3))就得到(1 2 3)。
o (cons list matrix)的目的是把函数list“注入”到表达式矩阵的表里。比方说，(cons list ‘((1 2 3) (4 56))就得到(list (1 2 3) (4 5 6)) 。这是什么？对了，我们轻而易举地在执行时生成了代码！
o 最后的函数应用(apply map 。。。)就清楚了。用样例最好说明：假设我们的矩阵matrix等于((1 2 3) (4 5 6))，那(cons list matrix)得到列表(list (1 2 3) (4 5 6))。自然地，(apply map (cons list matrix))等于(apply map ‘(list (1 2 3) (4 5 6))，也就等于(map list (1 2 3) (4 5 6))。计算这个表达式，当当！我们得到最后结果((1 4) (2 5) (3 6))。转置完毕。
§ 在处理树状数据时，我们往往须要知道树的最大深度（最大深度也叫树的高度）。一个节点的深度等于该节点到根节点间的路径数。下图中的树最大深度为3， 路径是A->D->F->H。如今我们写一个函数来计算一棵树的深度。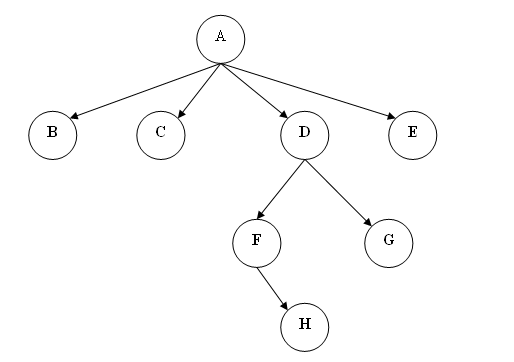 
o 先得知道树的表式方式。我们就用前面提到的表示法：(A B C (D (F H) G) E)。
o 应用高端函数和递归，我们的函数定义很easy：
o 解释下出现的新函数：
o keywordcond是条件函数，相当于C语言里的switch…case。它的语法例如以下： (cond ((条件1) (表达式1)) ((条件2) (表达式 2)) 。。。 ((条件 n) (表达式 n)) (else (表达式 n+1))) 也就是说，当(条件 k)的计算结果为真时，（表达式 k）会被运行。运行完后，函数cond结束。最后的符号else是特殊元素，它的计算结果总是为真，这保证了当其他条件语句不为真时，else相应的表达式肯定会被运行。
o 函数list?推断它的參数是否是列表。假设是，它返回真值，#t。不然返回假值#f。比方说，(list? ‘()) 返回 #t， (list? ‘(1 2))也返回#t，而(list? 1)返回#f。
o 这个函数怎么运行，就留给老大们当练习题吧。
假设Scheme里仅有高端函数，到如今也就不足为奇。非常多语言都已支持函数编程。Python, Perl，Ruby，C#3.0都内建了各式函数编程的功能，更不必说其他的函数编程语言，比方Erlang, Haskell, OCaml等。甚至C++里都用模板搭出了一整套函数编程的类库（比方boost.lambda）。只是Scheme另一套至今无可比拟的独门暗器：宏。说到宏，用C的老大们就笑了。用C++的老大们也笑了。好在此宏非彼宏。Scheme的宏和模板直接操作列表，根本就是Scheme语言的一部分，能够结合环境生成灵活的代码，甚至扩展Scheme故有的语法。
我们先用一个网上随处可见的样例说明C里宏的局限。如果我们须要写一个通用的求平方函数：x*x: y*y直观的写法应该是 #define SQAURE(x) x * x
假设真这样写，就错了。假设我们计算 1/SQUARE(2)，宏展开为1/2*2。结果我们得到1，而不是正确的1/4。于是我们改写一下总能够了吧： #define SQUARE(x) (x*x)
还是不行！看这个样例：SQUARE(1+1)，展开后变成(1+1*1+1)，结果得到错误的3。于是我们把宏改写成 #define SQUARE(x) ((x)*(x))
但这样还是不行。SQUARE(x++)会被展开成((x++)*(x++))，x被错误地多递增了一次。所以我们再改： int temp; #define SQUARE(x) ({temp = x; temp * temp}) 但是这种话这个宏仅仅能接受整数，还引入一个全局变量，那我们还不如写成int square(x){return x * x;}。于是再改： #define SAUARE(x) /
({typedef xtype =XTYPE x; xtype temp = XTYPE x; temp*temp; }) 这下能够了，但我们以后不能直接申明int x了，得用XTYPE这个typedef定义的类型。一个如此简单的宏都要耗费这么多考量，那再复杂一点的呢？C++的模板好一些，只是看看Boost的实现，就知道C++模板最好留给类库程序猿
[11]。幸好，Scheme的宏提供了全然不同的体验。它让我们把编程中反复出现的模式抽象出来。这类抽象往往和详细应用有关，不适合在短小篇幅内举例。因此，我们用模拟其他语言的功能来举例。但不要误解Scheme的宏仅仅适合写编译器或者DSL。
先举个简单样例供老大们开牙。Perl和Ruby里有一方便的语言后置修饰，即把条件推断放到运行语句的后面。比方： print “x > y” unless y >= x
这相当于以下的语句： if(! (y >= x) ){ print “x > y” }
Scheme里没有unless这个关键词，也不能后置修饰条件。只是用上宏就不一样了：
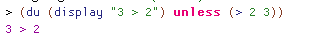
測试结果：
測试结果：
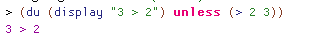
寥寥两三行，我们不仅有了unless这样的使用方法，还把它做成了后置修饰。宏是这样定义的：
§ 我们用函数define-syntax定义宏，du是这个宏的名字(do-unless的缩写)。缺省情况下，宏扩展从表达式的第一个元素開始，所以我加上du作为keyword。我们能够通过改动扩展宏的函数来去掉对起首keyword的依赖，只是这无关本质。
§ 每一个宏由一系列句法规则组成。这些句法规则由syntax-rules定义。函数syntax-rules规定了一到多组模式匹配的语句：(模式 模板)： (syntax-rules () (模式1 模板1) (模式2 模板2) 。。。 (模式n 模板n)) Scheme会依次用列出的模板匹配定义的表达式。匹配成功的话，就扩展模板。比方说当Scheme看到(du (display “3 > 2”) unless (> 2 3))时，就開始试着用宏定义里的模式来匹配该表达式。下划线”_”是一特殊字符，指代宏的名字。匹配的结果是 _ 与”du”匹配，expression与(display “3 > 2”)匹配，而condition与(> 2 3)匹配。匹配成功，所以这个模式相应的模板被展开为(if (not (> 2 3)) (display “3 > 2”))。运行该语句，便导致“3 > 2”被打印出来。两行程序，我们便能够体验新的编程手段。还不够酷么？
我们再看一个样例。Python和Haskell支持list comprehension，用相似集合定义的语句转换已知列表。比方以下的Python程序挑出从1到10里的奇数，并把将它们乘以2。最后的结果是[2, 6, 10, 14, 18]。 [2 * x for x in range(10) if x % 2 == 1] Haskell里甚至支持对多个列表同一时候操作。以下的样例表示，依次取出列表[1, 3, 5]里的每一个元素x，和列表[2, 4, 6]里的每一个元素y, 把他们组对。得到的结果是新的列表[(1,2),(1,4),(1,6),(3,4),(3,6),(5,6)] [(x,y) | x <- [1,3,5], y <- [2,4,6]] 我们用Scheme的宏能够如魔法般实现这样雅致的功能。Scheme类库Swindle里包括了花样繁复的list comprehension功能。我们这里仅仅实现一个阳春版的
[12]，用Philip Wadler提出的转换规则
[13]：
1991年Guy Lapalme给出了Common Lisp的lisp comprehension宏定义
[14]。熟悉Lisp的老大们能够看出Lisp的句法转换明显不如Scheme的方便简洁。以下是一些測试样例：
以下的是对这个宏的解释：
- flat-map是一个简单函数。它和函数map功能相似。只是它会展平嵌套的列表。比方说(map (lambda (x) (list x)) ‘(1 2 3))的结果是((1) (2) (3))，而把map换成flat-map得到的结果是(1 2 3)。
- (define-syntax list-of。。。定义了list comprehension的句法。当系统看见list-of时，就知道要运行list comprehension了。
- (syntax-rules (<-))表示開始定义句法转换规则。关键词syntax-rules后紧跟的列表(<-)能够包括一个或多个标识符。Scheme在句法转换时会自己主动忽略这些标识符，不会让它们同随后的变量匹配。
- 省略号…表示匹配0个或多个标识符号。比方，模式(x …)能够同(1)匹配，也能够同(1 2)匹配，也能够同(1 a 3)匹配。
- 注意定义的句法能够递归出现，比方list-of 就出如今随后的定义里。正是递归的威力让看似复杂的list comprehension变得如此easy实现。也就是说，Scheme的宏事实上是功能更为花哨的函数。
这篇帖子不能涵盖Scheme的所有功能。比方我们全然没有涉及continuation，延迟计算，或者尾递归。只是希望你领略到Scheme玲珑剔透的设计。学会它（更重要的，享受它），你会发现，一条通向计算机技术伊甸园的秘密小道出如今你脚下。
[1]
Alan Perlis, Epigrams of Programming, SIGPLAN Notices Vol. 17, No. 9(September 1982), pp7-13. Alan Perlis由于开发Algo编程语言获得1966年的图灵奖。Algo语言对命令式编程影响深远。流行多年的C，C++，和Pascal都属于Algo家族的成员。现下的热门Java和JavaScript尽管一个传承着Smalltalk的基因，一个根本就是Lisp的骨血，也要披着Algo家族句法风格的外衣。
[2] John K. Federaro, Lisp Is Chameleon,
Communications of the ACM, Volume 34, Issue 9(September 1991), pp27
，http://portal.acm.org/citation.cfm?doid=114669.114670 ACM非常不厚道，看这篇文章须要ACM的帐户。
[3] 号称是这篇文章说的：Howard Cannon, Flavors -- A Non-Hierarchical Approach to Object-oriented Programming. Unpublished draft, 1979, 1992, 2003。
[4] AOP（Aspect Oriented Programming）这个名词是AspectJ小组最先提出来的，但AOP的一些基本功能，比方说before/after/around操作，早就在Gregor的CLOS里实现了。
[5] John McCarthy, History of Lisp,
History of Programming Languages, 1978, pp173-185
，http://www-formal.stanford.edu/jmc/history/lisp/lisp.html
[6] John McCarthy, Recursive Functions of Symbolic Expression and Their Computation my Machine,
http://www-formal.stanford.edu/jmc/recursive/recursive.html
[7] Guy L. Steele, Richard P. Gabriel , Evolution of Lisp
, 1993.
[8] Richard Kelsey et., Revised
5 Report On the Algorithmic Language Scheme, 1998，
http://www.schemers.org/Documents/Standards/R5RS/r5rs.pdf
[9] A Conversation With Alan Kay， ACM Queue, Vol 2, No. 9, Dec/Jan 2004 – 2005.
http://acmqueue.com/modules.php?name=Content&pa=showpage&pid=273&page=1。Alan Kay真是人精。他的訪谈向来精彩。强烈推荐。麦克斯韦方程组是詹姆斯.麦克斯韦19世纪末总结(非原创)出的一套方程组，精炼地描写叙述了电场，磁场，电压，和电流间的关系。尽管方程组只是4个方程，却是经典电磁学的根基。
[10] John Hughs,
Why Functional Programming Matters,
http://www.math.chalmers.se/~rjmh/Papers/whyfp.html 。被众多老大推荐的经典论文。这篇文章出来，“黏合”的概念便广为传播。里面还有不少精彩样例，包含求解微分积分，和大小树剪枝。不是每一个人都对数学感兴趣。而大小树的样例又太长。不然他们都值得细述。
[11] 刘未鹏，《你应当怎样学习C++》，
http://blog.csdn.net/pongba/archive/2007/05/16/1611593.aspx
[13] Simon L Payton Jones,
Implementation of Functional Programming Languages, 1987,
http://research.microsoft.com/~simonpj/papers/slpj-book-1987/index.htm 规则在第7章。以下是代码相应的转换规则： flat-map f [] = [] flat-map f (x: xs) = (f x) ++ (flat-map f xs) (a) TE[[E | v<- L: Q]] = flat-map (lambda (v). TE[[E | Q]]) TE[L]
(b) TE[[E|B; Q]] = if TE[B] TE[[E|Q]] NIL
(c) TE[ [e |]] = Cons TE[E] NIL
这里E是表达式， B是返回布尔值的表达式，L是列表，Q是一个或多个生成器或B，而v表示变量。这里是一个样例：
TE( [x * x | x <- xs; x > 2])
ð flat-map (lambda x. TE([ x * x | x > 2])) xs
ð flat-map(lambda x. if (x > 2) then TE([x * x | ] ) nil) xs
ð flat-map(lambda x. if(x > 2) then (cons (x * x) nil) nil) xs
[14] Guy Lapalme,
Implementation of Lisp Comprehension Macro,
http://rali.iro.umontreal.ca/Publications/urls/LapalmeLispComp.pdf， 这篇论文里用了优化过的转换规则，而且通过改动reader macro, 让生成的宏识别通用的方括号[]，而不是象我们样例那用函数名list-of。只是呢，Common Lisp的宏要求我们手工完毕模板中代码的替换，所以随处可见准引號`, 取引號操作符,，和去引號兼列表剥除操作符,@。相比之下，Scheme的syntax-rule就清爽多了。人叫define-syntax而不是defmacro，并不是浪得虚名。
P.S., Jacky老大说这篇帖子不够生动，有妇联干部带三个表劝小夫妻不要离婚的严肃作派，并大方提供了范文。也一并帖在这里：
scheme！知道的明确是无数括号堆砌起来的一门语言