首尾相连的循环数组求其子数组最大值

结对成员

　　曹坤  翟凯

题目

　　返回一个整数数组中最大子数组的和。

要求：

　　输入一个整形数组，数组里有正数也有负数。

　　数组中连续的一个或多个整数组成一个子数组，每个子数组都有一个和。

　　如果数组A[0]……A[j-1]首尾相邻，允许A[i-1]， …… A[n-1]， A[0]……A[j-1]之和最大。

　　同时返回最大子数组的位置。

思路

　　经过讨论，只需将数组扩展为2倍长度，array[i]=array[length+i];从第一个元素开始依

次五个元素为一组，共分为五组进行；分别求得五个最大子数组和，然后求其最大值。这种方法

很容易解决问题，但是分组的个数就是元素的个数，即需要循环计算length次 。   不过，我偶

然间发现，最大子数组的第一个元素之前的元素一定是负数，否则整个数组全为正数，所以一个

在元素足够大的循环数组中，有一个比较节省计算量的方法，就是只需考虑负数元素的后一个元

素是否为正数，如果为正数则以此元素开始五个元素组成数组计算其最大值，即循环计算的次数

与负数的个数有关而无需循环length次。

代码

#include<iostream>

#include<conio.h>

#include<ctime>

#define Max_Length 10

using namespace std;

int main()

{ 

    srand((unsigned)time(NULL)); 

    int * arr=new int[2*Max_Length];

    int result=0,r,sum,k=0,l=0,g=0,a,b=0,flag=0;

    int randoms,count1=0,count2=0,c1=0,c2=0;

    

    while(1)

    {

        cout<<"随机产生"<<Max_Length<<"个数值:\n"<<endl;

        for ( int i=0; i<Max_Length; i++ ) {

            randoms = ( -rand()%100 + ( rand()%100 ));

            arr[i] = arr[i+Max_Length] = randoms;

            cout<<"数组元素"<<i+1<<"分别为:"<<arr[i]<<endl;

        }



        for(int s=0; s<Max_Length; s++) {

            

            if(arr[s]<0 && g==s) {

                g++;

                if(a<arr[s])

                {

                    a=arr[s];

                }

                if(g==Max_Length)

                {

                    cout<<"最大数组之和:"<<a<<endl<<endl;

                }

            }

            if(arr[s]>0 && l==s) {

                l++;

                b+=arr[s];

                if(l==Max_Length)

                {

                    cout<<"最大数组之和:"<<b<<endl<<endl;

                }

            }



            if(arr[s]<0 && arr[s+1]>=0) {

                flag=1;

                r=arr[s+1];

                sum=0;

                for ( int t=0,j=s+1; j<s+Max_Length+1; j++ ) {

                    t++;

                    if ( sum>=0 )

                    { sum+=arr[j]; }

                    else 

                    { c1=j; sum=arr[j]; }

                    if( r < sum ) {

                        count1=c1;

                        count2=c2;

                        r=sum;    

                    }

                }

                if(result<r)

                {

                    result=r;



                }

                

            }

        }

        if(flag==1)

            cout<<"最大数组之和3:"<<result<<endl<<endl;

        result=a=b=arr[0];

        getch();

    }

    return 0;

}

截图

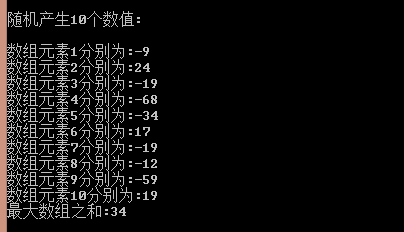
总结
我和同伴其实早就想到之前的解决方法了，这个是我自己最后想到的，在数组元素足够大时，

会有效地节省计算的次数。所以我认为，方法总是有的，但要找到更好的方法需要多思考才行。