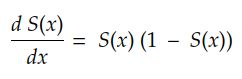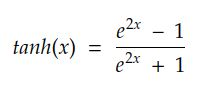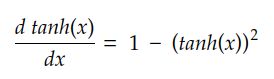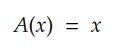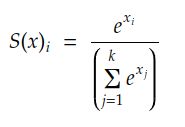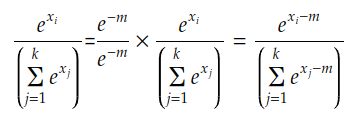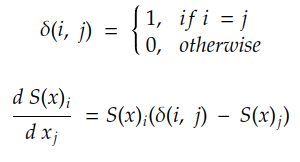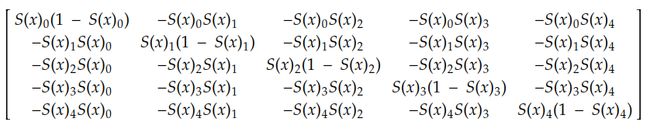现代C++中的从头开始深度学习：激活函数

一、说明

        让我们通过在C++中实现激活函数来获得乐趣。人工神经网络是生物启发模型的一个例子。在人工神经网络中，称为神经元的处理单元被分组在计算层中，通常用于执行模式识别任务。

        在这个模型中，我们通常更喜欢控制每一层的输出以服从一些约束。例如，我们可以将神经元的输出限制为 [0， 1]、[0， ∞] 或 [-1，+1] 的区间。另一个非常常见的场景是保证来自同一层的神经元总是相加 1。应用这些约束的方法是使用激活函数。

在这个故事中，我们将介绍 5 个重要的激活函数：sigmoid、tanh、ReLU、identity 和 Softmax。

二、关于本系列

在本系列中，我们将学习如何仅使用普通和现代C++对必须知道的深度学习算法进行编码，例如卷积、反向传播、激活函数、优化器、深度神经网络等。

这个故事是：C++中的激活函数

查看其他故事：

0 — 现代C++深度学习编程基础

1 — 在C++中编码 2D 卷积

2 — 使用 Lambda 的成本函数

3 — 实现梯度下降

...更多内容即将推出。

三、sigmoid激活

从历史上看，最著名的激活是Sigmoid函数：

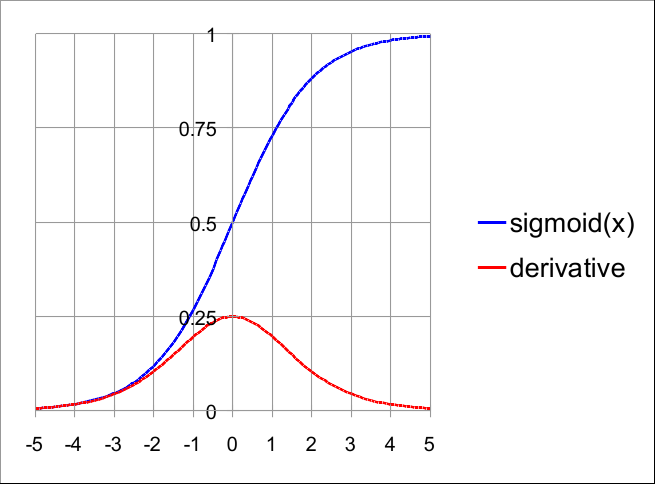
Sigmoid 函数和一阶导数

此图表显示了 sigmoid 的三个重要属性：

• 其输出限制在 0 和 1 之间;
• 它是平滑的，或者用更好的数学术语来说，它是可微分的;
• 它是S形的。

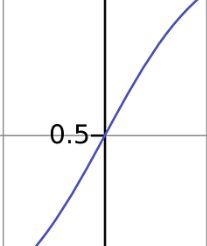
你应该想知道为什么形状很重要？S 形模型意味着曲线类似于原点邻域中的线性曲线：

这有助于更快地收敛小输入。有两种方法可以定义 sigmoid 公式：

这两个公式是等效的，但在实现时，我们更愿意使用后者：

double sigmoid(double x)
{
    return 1. / (1. + exp(-x));
}

我们更喜欢第二个公式的原因是第一个公式在数值上更不稳定。很多时候，我们在实现 sigmoid 时使用短路：

double sigmoid(double x)
{
    double result;
    if (x >= 45.) result = 1.;
    else if (x <= -45.) result = 0.;
    else result = 1. / (1. + exp(-x));
    return result;
}

这节省了大量处理并避免了以下情况 |x|很大。

四、sigmoid导数

        使用链式法则，我们可以找到 sigmoid 导数为：

        为方便起见，我们将 sigmoid 及其一阶导数分组为一个函子：

class Sigmoid : public ActivationFunction
{
    public:

        virtual Matrix operator()(const Matrix &z) const
        {
            return z.unaryExpr(std::ref(Sigmoid::helper));
        }

        virtual Matrix jacobian(const Vector &z) const
        {
            Vector output = (*this)(z);

            Vector diagonal = output.unaryExpr([](double y) {
                return (1. - y) * y;
            });

            DiagonalMatrix result = diagonal.asDiagonal();

            return result;
        }

    private:

        static double helper(double z)
        {
            double result;
            if (z >= 45.) result = 1.;
            else if (z <= -45.) result = 0.;
            else result = 1. / (1. + exp(-z));
            return result;
        }

};

我们将看到在介绍反向传播算法时如何使用激活函数导数。

Sigmoid 主要用于二元分类器或回归系统的输出层，其中结果始终为非负。如果输出可以是负值，请考虑使用下面描述的 Tanh 激活。

五、Tanh 激活

        顾名思义，tanh 激活由双曲正切三角函数定义：

        与 sigmoid 一样，tanh 也是 S 形且可微的。然而，tanh 的界限是 -1 和 1：

Tanh 函数和一阶导数

tanh 激活和 sigmoid 激活紧密相关：

请注意，由于 tanh 可以输出负值，因此我们不能将其与 logcosh 等损失函数一起使用。

tanh 的一阶导数为：

我们可以将 tanh 及其导数打包到一个函子中：

class Tanh : public ActivationFunction
{
    public:

        virtual Matrix operator()(const Matrix &z) const
        {
            return z.unaryExpr(std::ref(tanh));
        }

        virtual Matrix jacobian(const Vector &z) const
        {
            Vector output = (*this)(z);

            Vector diagonal = output.unaryExpr([](double y) {
                return (1. - y * y);
            });

            DiagonalMatrix result = diagonal.asDiagonal();

            return result;
        }
};

六、RELU

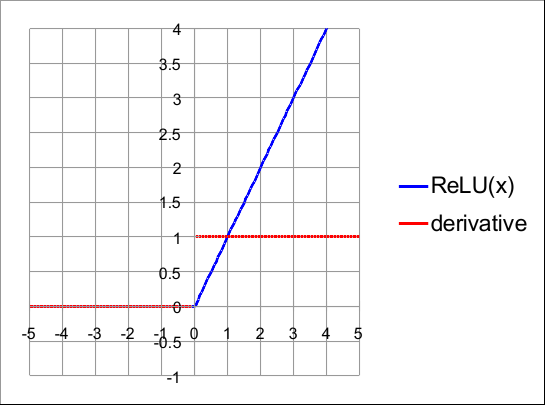
        Sigmoid 和 Tanh 的一个问题是它们的计算成本非常高，使得训练时间更长。ReLU是一个简单的激活：

ReLU活化和一阶导数

由于ReLU是一个简单的比较，因此与其他函数相比，其计算成本非常低。

我们可以按如下方式实现 ReLU：

class ReLU : public ActivationFunction
{

    public:

        virtual Matrix operator()(const Matrix &z) const
        {
            return z.unaryExpr([](double v) {
                return std::max(0., v);
            });
        }

        virtual Matrix jacobian(const Vector &z) const
        {

            Vector output = (*this)(z);
            Vector diagonal = output.unaryExpr([](double y) {
                double result = 0.;
                if (y > 0) result = 1.; 
                return result;
            });

            DiagonalMatrix result = diagonal.asDiagonal();

            return result;
        }

};

        相关要点是：

• 它对负值有界，但对正 x 值未绑定：[0， ∞]
• 当 x = 0 时，它是不可微分的。在实践中，我们通过假设当 x = 0 时导数 dRelu（x）/dx 为 0 来放宽此条件。

        由于 ReLU 基本上由单个比较组成，因此我们谈论的是一个非常快速的计算操作。它的第一阶导数也可以快速计算：

        尽管有其优点，但ReLu有三个主要缺点：

• 由于它不是正有界的，我们不能使用它来控制输出到 [0， 1]。正因为如此，在实践中，ReLU通常只存在于内部（隐藏）层中。
• 由于 ReLu 对于任何 x < 0 都是 0，有时我们的模型在训练过程中只是“死亡”，因为部分或所有神经元都停留在仅输出 0 的状态。
• 由于 ReLU 的导数在 x = 0 时不连续，因此对于某些输入，模型的训练可能不稳定。

有一些替代方法可以解决这些问题（参见Softplus，leakyReLU，ELU和GeLU）。然而，由于相当大的好处，ReLU仍然广泛用于现实世界的模型。

七、身份激活

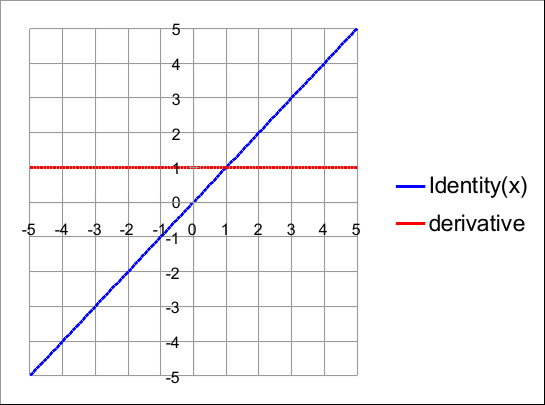
        身份激活的定义很简单：

        其导数为：

        使用身份激活意味着神经元的输出不会以任何方式被修改。在这种情况下，实现非常简单：

class Identity : public ActivationFunction
{
    public:
        virtual Matrix operator()(const Matrix &z) const { return z; }

        virtual Matrix jacobian(const Vector &z) const
        {

            Vector diagonal = Vector::Ones(z.rows());

            DiagonalMatrix result = diagonal.asDiagonal();

            return result;
        }
};

恒等式和一阶导数

八、softmax

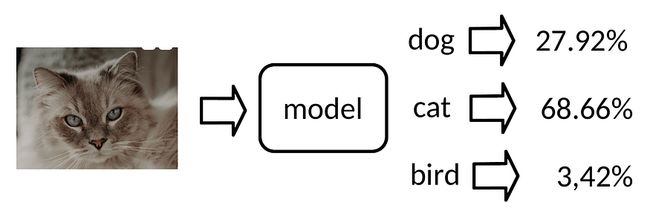
        考虑到我们有一张宠物的照片，我们需要确定它是哪种动物：狗？一只猫？仓鼠？一只鸟？豚鼠？在机器学习中，我们通常将此类问题建模为分类问题，并将模型称为分类器。

        Softmax非常适合作为分类器的输出，因为它实际上表示离散概率分布。例如，请考虑以下示例：

猫、狗和鸟的分类器

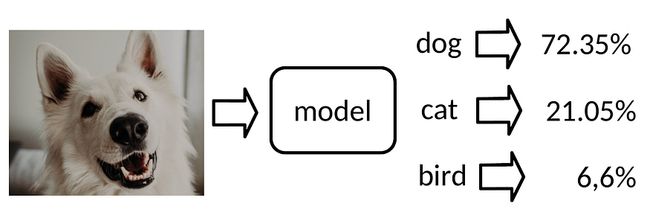
在前面的示例中，网络非常确定图像中的宠物是猫。在下一个示例中，模型将图像评分为狗：

在深度学习模型中，我们使用 Softmax 来表示这种类型的输出。

这张惊人的宠物照片是由Amber Janssens拍摄的

8.1 定义SoftMax

        Softmax的原始公式是：

        这个公式意味着，如果我们有 k 个神经元，第 i 个神经元的输出由 x i 的指数除以每个神经元 xj 的指数之和给出。

Softmax的第一个实现可以是：

const auto buggy_softmax(const Vector &z) {

    Vector expo = z.array().exp();
    Vector sums = expo.colwise().sum();
    Vector result = expo.array().rowwise() / sums.transpose().array();
    return result;

};

我们很快就会看到这种实现存在严重缺陷。但是这段代码的工作是说明softmax最重要的方面：每个神经元的结果取决于每个单独的输入。

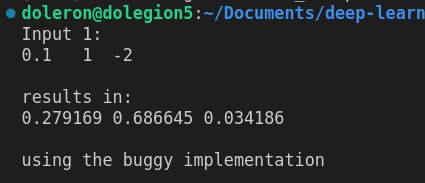
我们可以运行以下代码：

Vector input1 = Vector::Zero(3);
input1 << 0.1, 1., -2.;

std::cout << "Input 1:\n" << input1.transpose() << "\n\n";
std::cout << "results in:\n" << buggy_softmax(input1).transpose() << "\n\n";

到输出：

Softmax最重要的两个方面是：

• 所有神经元的总和始终为 1
• 每个神经元值在区间 [0， 1] 内

8.2 实现SoftMax

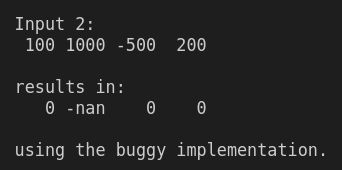
        我们之前的 softmax 实现的问题在于指数函数增长非常快。例如，e¹⁰ 大约是 22，026，但 e¹⁰⁰ 是 2.688117142×10 ⁴³，这是一个令人生畏的巨大数字。事实证明，即使我们使用适度的数字作为输入，我们的实现也会失败：

Vector input2 = Vector::Zero(4);
input2 << 100, 1000., -500., 200.;

std::cout << "Input 2:\n" << input2.transpose() << "\n\n";
std::cout << "results in:\n" << buggy_softmax(input2).transpose() << "\n\n";
std::cout << "using the buggy implementation.\n";

        发生这种情况是因为C++浮点具有固定的表示形式。使用常规 64 位处理器，任何通过 750 或更多字符的调用都会导致数字。cmath exp(x)inf

        幸运的是，我们可以使用以下技巧来修复它：

        其中 m 是最大输入：

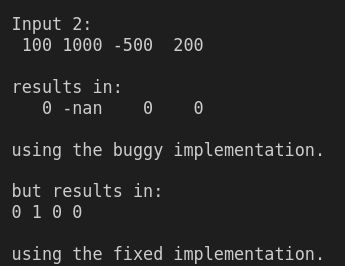
        现在，通过修复代码，我们得到：

const auto good_softmax(const Vector &z) {

    Vector maxs = z.colwise().maxCoeff();
    Vector reduc = z.rowwise() - maxs.transpose();
    Vector expo = reduc.array().exp();
    Vector sums = expo.colwise().sum();
    Vector result = expo.array().rowwise() / sums.transpose().array();
    return result;

};

溢出是数值不稳定的一个来源。

当我们开发现实世界的深度学习系统时，数值稳定性是一个非常普遍的问题。

8.3 Softmax衍生产品

        Softmax和其他激活之间存在非常明显的差异。通常，像sigmoid或ReLU这样的激活是系数操作，即一个系数的值不会影响其他系数。当然，在 Softmax 中，这不是真的，因为所有值都需要求和 1。这种依赖性使得softmax导数的计算有点棘手。尽管如此，经过一点点的计算并使用我们的老朋友链规则，我们可以弄清楚：

如果您想阅读此衍生品的发展，请告诉我。

例如，如果我们有 5 个神经元，则每个神经元相对于同一层中每个神经元的导数由下式给出：

这个导数将在下一个故事中应用，当我们训练第一个分类器时。

九、包装SoftMax以供进一步使用

最后，我们可以按如下方式实现 Softmax 函子：

class Softmax : public ActivationFunction
{
    public:

        virtual Matrix operator()(const Matrix &z) const
        {

            if (z.rows() == 1)
            {
                throw std::invalid_argument("Softmax is not suitable for single value outputs. Use sigmoid/tanh instead.");
            }
            Vector maxs = z.colwise().maxCoeff();
            Matrix reduc = z.rowwise() - maxs.transpose();
            Matrix expo = reduc.array().exp();
            Vector sums = expo.colwise().sum();
            Matrix result = expo.array().rowwise() / sums.transpose().array();
            return result;
        }

        virtual Matrix jacobian(const Vector &z) const
        {
            Matrix output = (*this)(z);

            Matrix outputAsDiagonal = output.asDiagonal();

            Matrix result = outputAsDiagonal - (output * output.transpose());

            return result;
        }

};

如今，几乎每个分类器都在输出层中使用 Softmax。我们将在接下来的故事中介绍softmax的一些真实示例。

十、其他激活函数

        还有其他几个激活函数。除了这里描述的那些，我们还可以列出Softplus，Softsign，SeLU，Elu，GeLU，指数，swish等。一般来说，它们是sigmoid或ReLU的一些变体。

十一、结论和下一步

        激活函数是机器学习模型最重要的构建块之一。在这个故事中，我们学习了一些最重要的：Sigmoid，Tanh，ReLU，Identity和Softmax。

        在下一个故事中，我们将深入探讨最重要的深度学习算法的实现：反向传播。从零开始，在C++和本征。