Dubins曲线学习笔记及相关思考

   本篇博客主要记录在学习Dubins曲线过程中的笔记及相关思考和概括总结

一、主要参考资料
     1、Andy G’s Blog：【点击此处跳转】
     2、Andy G’s Blog的PDF版本：【点击此处跳转】
     3、Andy G’s Blog提供的配套c++程序：【点击此处跳转】

     Andy G’s Blog介绍的主要内容：Dubins的情景引入及介绍、单车运动学模型、Dubins曲线的高级描述、 Dubins曲线的轨迹求解（核心部分）

     4、论文Classification of the Dubins set的PDF版本：【点击此处跳转】
     5、与上述论文介绍方法配套的MATLAB程序：【点击此处跳转】
     6、与上述论文介绍方法配套的笔记：【点击此处跳转】

     论文Classification of the Dubins set中给出了不同于Andy G’s Blog的另一种方法

     注：上述开源程序链接均为GitHub链接，打不开的可以多试几次

---

二、参考资料内容纠正
     Andy G’s Blog中存在一些明显的错误，我做了一些纠正，如下图所示：

---

三、Dubins曲线的轨迹计算

     1、Dubins曲线的构成

     Dubins曲线是在满足曲率约束和规定的始端和末端的切线方向的条件下，连接两个二维平面（即X-Y平面）的最短路径，并假设车辆行驶的道路只能向前行进。
     在1957年, Lester Eli Dubins (1920–2010) 证明任何路径都可以由最大曲率弧或直线段组成（两点之间的路径必须存在）。 换句话说，连接两点的最短路径将通过最大曲率的圆弧和直线段构成。
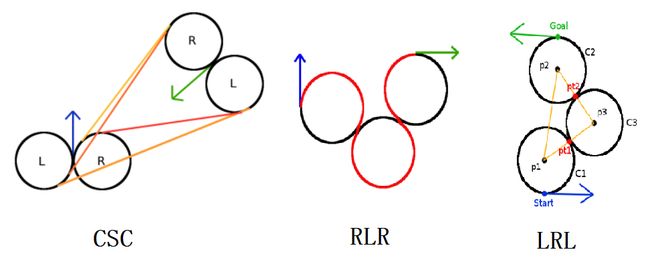
     经过证明，任意起点到终点的Dubins最短路径可以由不超过三个原始运动构成。由三个原始运动构成的序列称为一种轨迹。由于两个连续的、相同的原始运动可以合并为一个原始运动，并且Dubins证明最优的轨迹只能是以下6种组合之一，即RSR, LSL, RSL, LSR, RLR, LRL。前四种统称为CSC轨迹，后两种统称为CCC轨迹，其中原始运动R代表右转，S代表直行、L代表左转。

     CSC轨迹示例：

     CCC轨迹示例：

     2、轨迹计算的总体思路

     首先通过当前点和目标点的位姿计算出两个最大曲率圆的圆心（最大曲率由车辆的最小转弯半径决定），接下来计算切点，对于RSR和LSL曲线要计算两个最大曲率圆的外切线的切点，对于RSL和LSR曲线要计算两个最大曲率圆的内切线的切点，对于RLR和LRL曲线要计算第三个圆的位置及三个圆之间的接触点。以上切点也就是三段原始运动的衔接点。

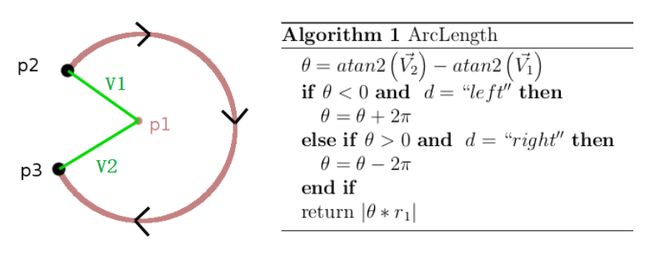
     然后通过得到的切点计算弧长及切线长度，弧长通过L=Rθ计算，也就是θ计算，此处不能简单的使用余弦定理计算，因为轨迹中需要的可能是长弧，可通过atan2（v2）- atan2（v1）计算，因其计算结果带正负，再结合轨迹的方向判断是否要加上或减去2π，来得到真实的角度θ，从而得到弧长，对于CSC曲线的切线部分直接通过两点间距离公式计算即可

     现在已经得到了轨迹中三段原始运动的轨迹长度，此时只要能够计算出各段轨迹对应的运动时间，就可以控制车辆按照规划的轨迹运动，比如对于RSR轨迹而言，让车辆先以最小转弯半径右转t1s，再直行t2s，再以最小转弯半径右转t3s
     Dubins车辆的运动速度认为是恒定的，弧线部分的运动时间，可以通过将弧线切分成若干段小直线段，然后通过欧拉积分来计算弧线的运动时间，Andy G’s Blog中介绍通常小直线段的长度取[0.01,0.05] ，取值越小越精确

     3、切点计算思路

     Dubins曲线轨迹计算的核心之一是切点的计算，Andy G’s Blog中介绍了CSC轨迹用几何法和向量法求解切点的方法，以及CCC轨迹第三个圆位置及接触点的方法，这里做一下概括
     （1）几何法求CSC轨迹内切点
     首先，以两个最大曲率圆的圆心之间连线(即向量v1)距离为直径，连线中点为圆心构造圆C3，以r1+r2为半径，p1为圆心构造圆c4。圆c3与c4交点为pt（上下各一个，分别用来求两条内切线，下图仅标注了上面那个），三角形p1p3p4的三边均已知，利用余弦定理可求出角ptp1p3，利用atan2（v1）可求出向量v1与x轴夹角，这个夹角再加上角ptp1p3，即可得到向量v2与x轴夹角θ（v2为pt-p1），且向量v2的长度已知为r1+r2，通过向x和y轴投影，再加上p1点坐标已知，便可计算出pt点坐标
     pt点坐标计算出来后，向量pt-p1便已知且与向量p_it1-p1仅长度不同，很容易计算出点p_it1的坐标，也就是第一条内切线位于圆c1上的切点，很容易得出第一条切线等价于向量p2-pt，点pt、p2、p_it1坐标均已知，很容易计算出第一条切线位于圆c2上的切点，利用同样的方法可以计算出另一条内切线的切点。

     （2）几何法求CSC轨迹外切点

     几何法求CSC轨迹外切点的方法与求内切点类似，不同的是在构造圆c4的时候半径取为r1-r2，Andy G’s Blog中假设r1>=r2，然而简单思考便可知r1=r2时以上方法并不适用，Andy G’s Blog中并没有给出此时的计算方法，其实当r1=r2时比我们预想的要简单，见（3）

     （3）r1=r2时CSC轨迹外切点求法

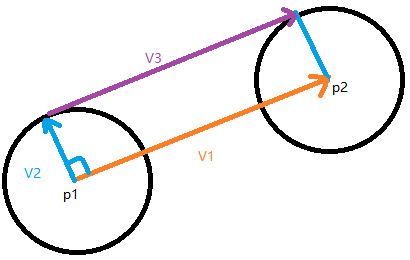
     方法1：向量v2与v1间夹角为90度，再加上atan2（v1）即可得到向量v2与x轴夹角，从而求出第一条外切线位于c1上的切点，同理可得c2上的切点，c2上的切点也可由向量v1与v3等价求得。
     方法2：将向量v1单位化，并旋转90度，便得到了与向量v2方向相同的单位向量，乘以向量v2的长度即r1，在加上p1点坐标，便可得到第一条外切线在c1上的切点，第一条外切线在c2上的切点，可由v1与v3等价求得，同理可求出第二条外切线的切点

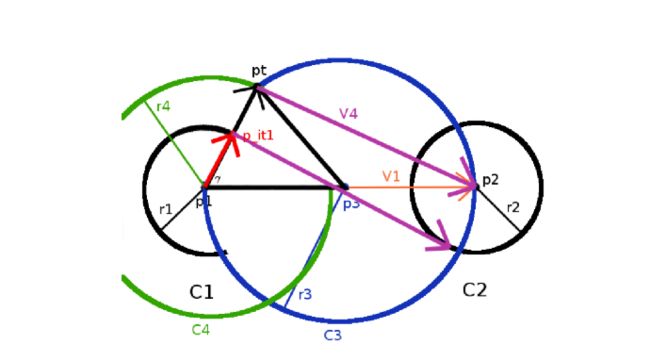
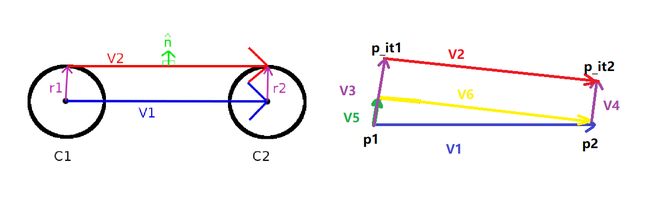
     （4）向量法求CSC轨迹外切点

     Andy G’s Blog中给出了下面的左图，我根据理解绘制了更加详细的右图，为了突出向量间的变化省去了两个圆
     此时，同样假设r1>r2,r1=r2时的求法见（3），首先假设与向量v2垂直的单位向量n，单位向量n与向量v3、v4、v5方向相同，可知向量n与向量v6垂直，向量v6可由v1-v5求得，其中v5又可以由（r1-r2）乘以单位向量n表示，由单位向量n与向量v6点积为0，可得到cos∠p2p1p_it1=（r2-r1）/D,其中D为向量v1的模，为了方便将（r2-r1）/D记作c，为已知量，将向量v1单位化，并旋转∠p2p1p_it1度便可以得到单位向量n，乘以r1，再加上p1，便可得到切点p_it1的坐标，利用向量v2与v6等价，便可得到切点p_it2的坐标，同理可得另一条外切线坐标

     （5）向量法求CSC轨迹内切点

     向量法求CSC轨迹内切点的方法与求外切点类似，不过向量V5的长度由r1-r2变为了r1+r2，从而cos∠p2p1p_it1=（r2+r1）/D，示意图如下所示，加上一个棕色的T形，再画上几道风，是不是很像一辆疾驰的自行车 (｡◕ˇ∀ˇ◕)？该画出自极简抽象派画者-慕羽ヾ(◍°∇°◍)ﾉﾞ

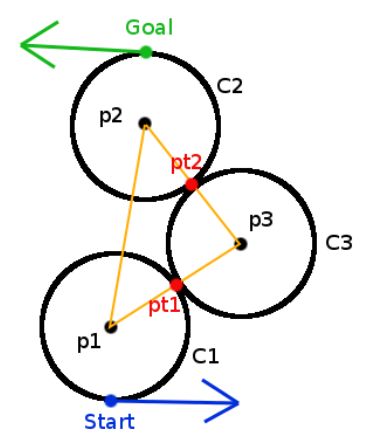
     （6）CCC轨迹切点

     首先通过余弦定理求出∠p2p1p3，然后通过atan2（v1）求出向量v1（向量v1即p2-p1）距离x轴角度θ，对于RLR轨迹，应该在θ的基础上加上∠p2p1p3，对于LRL轨迹应该在θ的基础上减去∠p2p1p3，从而得到向量p3-p1距离x轴的夹角，从而计算出p3的坐标，有了p3的坐标，很容易通过比例由向量p3-p2、向量p3-p1分别计算出切点pt2和pt1的坐标，下图为一个LRL的例子

     关于CCC轨迹，需要强调的是当前点和目标点必须彼此接近才能使三个圆圈的这种排列成为可能。Andy G’s Blog中提到当前点和目标点之间距离小于4r，则CCC曲线有效。若等于4r，则CSC轨迹更佳。若c3圆的半径与c1和c2则采用其他四种轨迹更优

四、论文Classification of the Dubins set介绍方法的计算思路

     注：本部分仅对结论和思路进行整理，推导过程可见文章第一部分给出参考资料6

     论文Classification of the Dubins set中介绍了，另一种求解Dubins曲线的思路，为方便计算，在计算前先进行了坐标变换，设起点为s（xi，yi，αi） ， 终点为g（xg，yg，βg） ，先将起点平移支原点，并放置 θ 角，则终点也落在 x 轴上，变换后起点和终点的坐标为 s（0，0，α）和g（d，0，β）

     这里将最小转弯半径正则化为1，这样每个最小转弯半径都为1，由角度计算弧长时更方便，弧长即等于角度（弧度制）

     本部分内容对应的MATLAB程序如下（首行在dubins_core.m文件66行左右）：

    dx = p2(1) - p1(1);
    dy = p2(2) - p1(2);
    D = sqrt( dx^2 + dy^2 );
    d = D / r;                  % distance is shrunk by r, this make lengh calculation very easy
    theta = mod(atan2( dy, dx ), 2*pi);
    alpha = mod((p1(3) - theta), 2*pi);
    beta  = mod((p2(3) - theta), 2*pi);

     做完以上变换就可以开始计算了，要强调的一点是变换后，长度的衡量单位不再是1，而是最小转弯半径R，比如起点和终点间距离为D，但在后续计算中均 使 用 d = D/R来计算
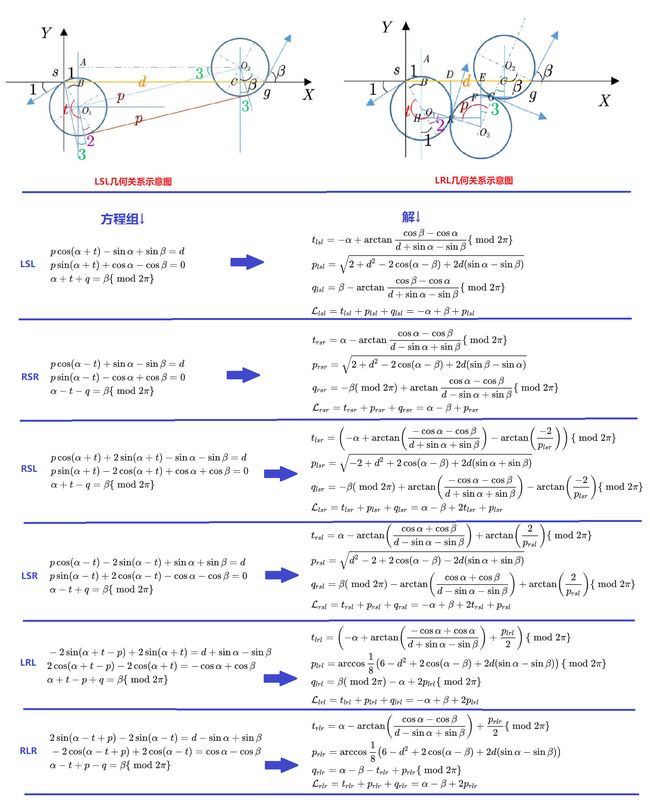
     计算方法是对于每种轨迹，均单独进行分析，并寻找其之间的几何关系，列等式解方程组，直接计算出每种轨迹对应的三段轨迹的长度，如下所示（拖拽或点击可查看大图）

     本部分内容对应的MATLAB程序如下（首行在dubins_core.m文件108行左右）

function param = dubins_LSL(alpha, beta, d)
    tmp0 = d + sin(alpha) - sin(beta);
    p_squared = 2 + (d*d) -(2*cos(alpha - beta)) + (2*d*(sin(alpha) - sin(beta)));
    if( p_squared < 0 )
        param = [-1, -1, -1];
        return;
    else
        tmp1 = atan2( (cos(beta)-cos(alpha)), tmp0 );
        t = mod((-alpha + tmp1 ), 2*pi);
        p = sqrt( p_squared );
        q = mod((beta - tmp1 ), 2*pi);
        param(1) = t; 
        param(2) = p; 
        param(3) = q;
        return ;
    end
end
function param = dubins_LSR(alpha, beta, d)
    p_squared = -2 + (d*d) + (2*cos(alpha - beta)) + (2*d*(sin(alpha)+sin(beta)));
    if( p_squared < 0 )
        param = [-1, -1, -1];
        return;
    else
        p    = sqrt( p_squared );
        tmp2 = atan2( (-cos(alpha)-cos(beta)), (d+sin(alpha)+sin(beta)) ) - atan2(-2.0, p);
        t    = mod((-alpha + tmp2), 2*pi);
        q    = mod(( -mod((beta), 2*pi) + tmp2 ), 2*pi);
        param(1) = t; 
        param(2) = p; 
        param(3) = q;
        return ;
    end
end
function param = dubins_RSL(alpha, beta, d)
    p_squared = (d*d) -2 + (2*cos(alpha - beta)) - (2*d*(sin(alpha)+sin(beta)));
    if( p_squared< 0 ) 
        param = [-1, -1, -1];
        return;
    else
        p    = sqrt( p_squared );
        tmp2 = atan2( (cos(alpha)+cos(beta)), (d-sin(alpha)-sin(beta)) ) - atan2(2.0, p);
        t    = mod((alpha - tmp2), 2*pi);
        q    = mod((beta - tmp2), 2*pi);
        param(1) = t;
        param(2) = p; 
        param(3) = q;
        return ;
    end
end
function param = dubins_RSR(alpha, beta, d)
    tmp0 = d-sin(alpha)+sin(beta);
    p_squared = 2 + (d*d) -(2*cos(alpha - beta)) + (2*d*(sin(beta)-sin(alpha)));
    if( p_squared < 0 )
        param = [-1, -1, -1];
        return;
    else
        tmp1 = atan2( (cos(alpha)-cos(beta)), tmp0 );
        t = mod(( alpha - tmp1 ), 2*pi);
        p = sqrt( p_squared );
        q = mod(( -beta + tmp1 ), 2*pi);
        param(1) = t; 
        param(2) = p; 
        param(3) = q;
        return;
    end
end
function param = dubins_RLR(alpha, beta, d)
    tmp_rlr = (6. - d*d + 2*cos(alpha - beta) + 2*d*(sin(alpha)-sin(beta))) / 8.;
    if( abs(tmp_rlr) > 1)
        param = [-1, -1, -1];
        return;
    else
        p = mod(( 2*pi - acos( tmp_rlr ) ), 2*pi);
        t = mod((alpha - atan2( cos(alpha)-cos(beta), d-sin(alpha)+sin(beta) ) + mod(p/2, 2*pi)), 2*pi);
        q = mod((alpha - beta - t + mod(p, 2*pi)), 2*pi);
        param(1) = t;
        param(2) = p;
        param(3) = q;
        
        return;
    end
end
function param = dubins_LRL(alpha, beta, d)
    tmp_lrl = (6. - d*d + 2*cos(alpha - beta) + 2*d*(- sin(alpha) + sin(beta))) / 8.;
    if( abs(tmp_lrl) > 1)
        param = [-1, -1, -1]; return;
    else
        p = mod(( 2*pi - acos( tmp_lrl ) ), 2*pi);
        t = mod((-alpha - atan2( cos(alpha)-cos(beta), d+sin(alpha)-sin(beta) ) + p/2), 2*pi);
        q = mod((mod(beta, 2*pi) - alpha -t + mod(p, 2*pi)), 2*pi);
        param(1) = t;
        param(2) = p;
        param(3) = q;
        return;
    end
end

     得到轨迹中三段轨迹的长度后，还需要计算出三段轨迹之间的两个衔接点，依然采用了几何分析的方式，结论如下（拖拽或点击可查看大图）

     本部分内容对应的MATLAB程序如下（首行在dubins_curve.m文件226行左右）

function seg_end = dubins_segment(seg_param, seg_init, seg_type)
    L_SEG = 1;
    S_SEG = 2;
    R_SEG = 3;
    if( seg_type == L_SEG ) 
        seg_end(1) = seg_init(1) + sin(seg_init(3)+seg_param) - sin(seg_init(3));
        seg_end(2) = seg_init(2) - cos(seg_init(3)+seg_param) + cos(seg_init(3));
        seg_end(3) = seg_init(3) + seg_param;
    elseif( seg_type == R_SEG )
        seg_end(1) = seg_init(1) - sin(seg_init(3)-seg_param) + sin(seg_init(3));
        seg_end(2) = seg_init(2) + cos(seg_init(3)-seg_param) - cos(seg_init(3));
        seg_end(3) = seg_init(3) - seg_param;
    elseif( seg_type == S_SEG ) 
        seg_end(1) = seg_init(1) + cos(seg_init(3)) * seg_param;
        seg_end(2) = seg_init(2) + sin(seg_init(3)) * seg_param;
        seg_end(3) = seg_init(3);
    end
end

     以上公式除了可以计算轨迹间衔接点之外，还可以用来计算轨迹上的每个点，对于左转和右转，只需要改变t就可以求其他点，对于直行只需要改变p就可以求其他点，至此，我们可以求出轨迹上的任何需要的点，完成了Dubins曲线的生成