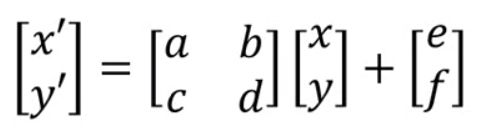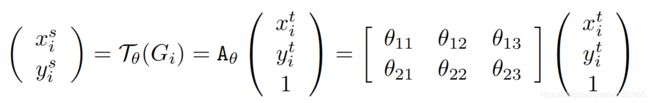STN(Spatial Transformer Networks)
上一篇介绍了通道注意力机制SENET,有兴趣的同学可以去看一下SENET。今天较少一篇空间上的注意力机制网络Spatial Transformer Networks(STN)。同样先上传一下原文地址:STN。STN是2016年发表在CVPR,其实它是在SENET之前发表的,但是SENET更容易理解,我就将它作为注意力机制的第一篇博客。相信看了上一篇博客的同学肯定对注意力机制有一定的了解了,那么本篇文章作为注意力机制的第二篇,即空间注意力机制。
卷积神经网络定义了一个非常健壮的模型,但仍然受到限制,缺乏以计算和参数有效的方式对输入数据进行空间不变的能力的应对。STN引入了一个新的可学习的空间转换模块,它可以使模型具有空间不变性。这个可微分模块可以插入到现有的卷积结构中,使神经网络能够在Feature Map本身的条件下自动地对特征进行空间变换,而无需任何额外的训练监督或优化过程的修改。
空间不变性
理解STN之前,先理解图像的不变性。
图像的不变形包括:
平移不变性:Translation Invariance
旋转/视角不变性:Ratation/Viewpoint Invariance
尺度不变性:Size Invariance
光照不变性:Illumination Invariance
用一个例子解释一下不变性,例如我们熟悉的平移不变性,请看下图:
平移不变性
我们总说CNN网络是具有平移不变性的,意思就是上面这只小年不管位置在哪我们都可以通过网络的训练来识别出来它是一只鸟,但是我们发现在移动输入样本的时候,模型预测结果时发生变化的,如上面这只小鸟,在右下角的时候甚至连类别有预测错误。我们做分类或者目标检测的时候,像上面这只小鸟,在居中、右下方或其它位置的时候,虽然我们都识别出来它是鸟,但是我们对模型的识别结果都是有差别的,我们举个简单的小例子来了解一下,为什么会模型的识别结果会有差别呢?
例如我们在网络的某一步输入数据位00110011,如下图所示:
上图中输入数据为00110011,经过步长为2的最大池化操作,则输出为0101。
将shift:0的输入数据项做平移一位,则shift:1的输入变为01100110,经过步长为2的最大池化之后输入为1111。
从上面的例子中可以看出,池化操作仅仅移动了以为,但是输出却有着天壤的差别。其实,导致CNN网络模型平移不变性损失的主要就是池化操作。《Making Convolutional Networks Shift-Invariant Again》提出了BlurPool方法,有效解决池化操作的平移不变性的问题,以后有机会再出一篇关于该论文的解释,这里就不再赘述了(这是B站上一个关于该论文的视频讲解,还是不错的)。这里只是为了说明现有的深度神经网络模型在空间上的不变性是有必要解决的一个问题。
李宏毅老师讲的STN是非常清晰的有兴趣的同学也可以看一下视频。
STN模型
我们回到STN模型中,我们的理想的模型中,特征空间转换之后,模型依然可以给出同样的正确结果,STN模型就是针对网络模型的空间不变性问题而生,使其具有更鲁棒的空间不变性。
STN模型效果
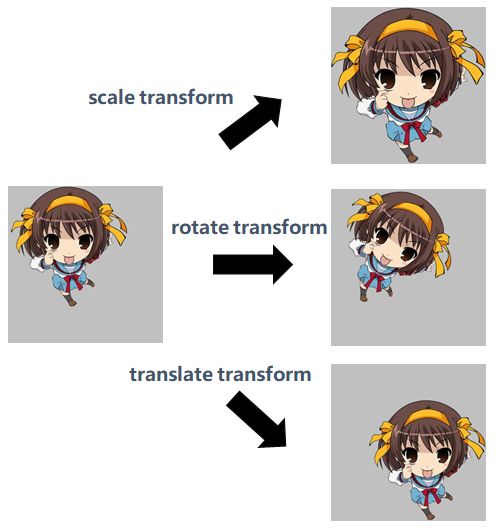
文章开头我们提到过,CNN中模型的空间不变性有:平移不变性、旋转不变性、尺度不变性,请看下面凉春宫日的图片更直观,分别是缩放、旋转、平移:
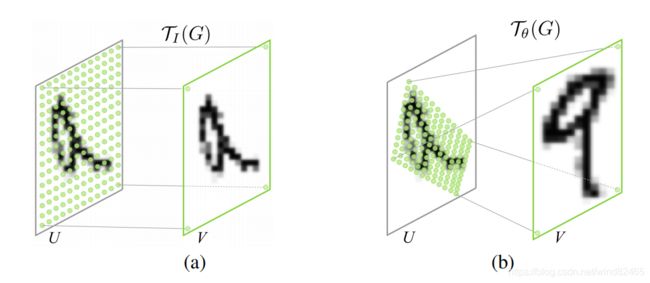
那么,再看一下STN效果是什么样的,我们用熟悉的MNIST举例:
上图中(a)是输入数据,(b)是STN模块,(c)是STN模块的输出。可以看出经过STN模块之后有效的将空间数据提取放大再传递给下一层。并且STN模块可以作为单独的模块嵌入到CNN网络中,所以它不止是针对输入图片,同样可以在任意的Feature Map中,增加网络鲁棒性和识别置信度。
STN模型
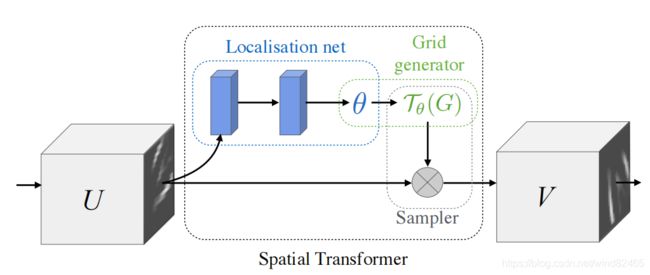
下图是ST模块的结构图:
ST模块有三个模块组成,分别是:Localisation net、Grid generator和Sampler,下面分别对其进行解释。
Localisation net
Localisation net以下简称L操作,从结构图可以看出,L操作的输入时U(U可以是输入图片也可以是Feature Map),经过L模块操作之后输出![]() 。L操作其实是经过了一系列的仿射变换得到
。L操作其实是经过了一系列的仿射变换得到![]() 。
。
是什么意思呢,其实就是L操作反应输入数据位置和输出位置的对应关系,那么这个仿射变换就是这个对应的公式,举例来说:
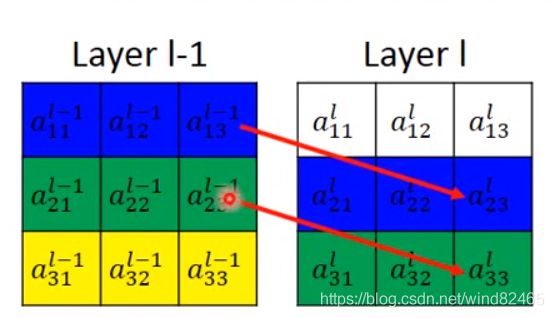
上图中,Layer l-1表示输入数据,Layer l表示输出层,红色箭头表示L操作的对应关系,它反应Layer l-1中的![]() 到Layer l中的
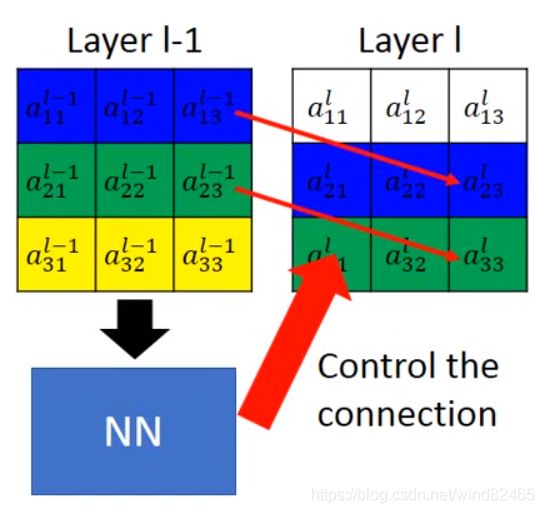
到Layer l中的![]() 是如何对应上的,它控制输出Feature和输入Feature在空间上的对应关系,也就是下面这张图,Layer l -1经过NN模块(L操作)转换成了Layer l。
是如何对应上的,它控制输出Feature和输入Feature在空间上的对应关系,也就是下面这张图,Layer l -1经过NN模块(L操作)转换成了Layer l。
我相信到这大家都会明白L操作的作用了,那么L是如何将经过移动的输出的Feature Map和输入对应上的呢?我们看下面这张图,这是一个放大2倍的操作![]() 表示输入Feature的一个坐标,
表示输入Feature的一个坐标,![]() 表示要放大的一个坐标:
表示要放大的一个坐标:
我们的目的就是将![]() 移动到
移动到![]() 处,那么矩阵乘法很好解决:
处,那么矩阵乘法很好解决:
经过矩阵相乘就可以方便的得到![]() 的坐标值,后面的[0,0]表示平移距离,这里为0表示没有平移,只有放大操作。
的坐标值,后面的[0,0]表示平移距离,这里为0表示没有平移,只有放大操作。
同理,我们也可以计算出下面这种缩小1/4,并且向右移0.5的操作:
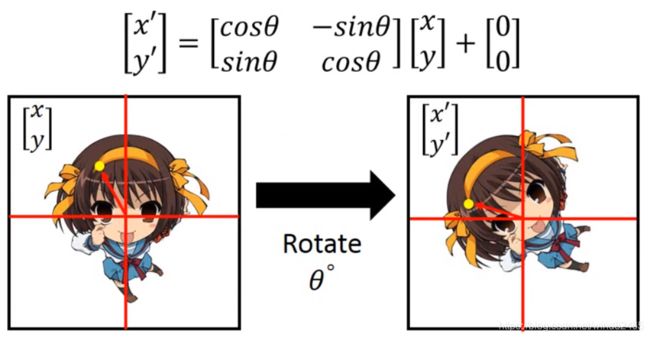
到此,我们就可以得到放大、缩小、平移的计算方法了,下面我们再看一下旋转计算方法,下图,又是凉春宫日:
上面三步我们就把空间不变性的相关都计算出来了,分别是缩放、平移和旋转,从上面三种情况的计算可以总结出来,我们的空间不变性与六个参数有关系,如下公式所示:
放大、缩小、旋转由a、b、c、d控制,e和f控制平移。到这里L操作我们就完成了。
L操作就是得到![]() = {a,b,c,d,e,f},得到这6个参数就是得到了输入和输出的Feature Map的映射关系。到此,L操作我们就基本讲完了,还有没明白的同学可以私信我。
= {a,b,c,d,e,f},得到这6个参数就是得到了输入和输出的Feature Map的映射关系。到此,L操作我们就基本讲完了,还有没明白的同学可以私信我。
注:对旋转不太了解的同学可以看一下下面的公式推导(仅做参考,可以跳过):
Grid generator
Grid generator以下简称G操作,G操作作用就是根据L得到的参数生成输入与输出Feature Map的对应关系,也就是将Feature Map通过 ![]() = {a,b,c,d,e,f}进行空间数据变换。如下图所示:
= {a,b,c,d,e,f}进行空间数据变换。如下图所示:
如上图所示,只管的反映出G操作的目的。(a)表示没有使用G操作,直接恒等映射得到的输出结果V。(b)是经过G的操作之后得到的输出结果V。明显可以看出,经过L和G的空间变换之后的结果更直观,更便于训练和识别。操作如下公式:
将输入的Feature Map的每个值与 ![]() = {a,b,c,d,e,f}进行矩阵乘法,得到输出结果V。也就是得到了输入U和输出V的对应关系。
= {a,b,c,d,e,f}进行矩阵乘法,得到输出结果V。也就是得到了输入U和输出V的对应关系。
Sample
Sample操作以下简称S操作。这里要回忆一下上面的L操作,我们对输入Feature Map进行空间变换,不知道有没有同学发现问题?想一想,想一想......
可能有的同学看出来了,就是L操作的例子中,我们得到的都是整数,输出的U可以和输入V的每个点一一对应。但是,如果出现小数怎么办呢?请看下面这个例子:
这个例子,取L的输出的六个参数为a = 0,b = 0.5,c = 1,d = 0,e = 0.6,f = 0.4。我们把Layer I的![]() 带入公式,就是上图中最上面的矩阵运算,得出Layer I对应的坐标为x = 2*0 + 2*0.5 + 0.6 = 1.6;y = 1*2 + 0*2 + 0.4 = 2.4。所以对应Layer I的
带入公式,就是上图中最上面的矩阵运算,得出Layer I对应的坐标为x = 2*0 + 2*0.5 + 0.6 = 1.6;y = 1*2 + 0*2 + 0.4 = 2.4。所以对应Layer I的![]() 对应Layer I -1的位置是[1.6,2.4]......呦呵,小数!ε=(´ο`*)))!唉,显然,这是无法对应我们要的坐标位置的。可能四舍五入得到[2,2]正好对应Lyaer I -1了,但是这真的能对应上我们的位置么?
对应Layer I -1的位置是[1.6,2.4]......呦呵,小数!ε=(´ο`*)))!唉,显然,这是无法对应我们要的坐标位置的。可能四舍五入得到[2,2]正好对应Lyaer I -1了,但是这真的能对应上我们的位置么?
我们再使用两个Layer I的位置![]() 和
和![]() 再计算一下Layer I-1对应的坐标,带入公式
再计算一下Layer I-1对应的坐标,带入公式
计算出对应的Layer I-1的位置(a = 0,b = 0.5,c = 1,d = 0,e = 0.6,f = 0.4):
(1)![]()
![]() = 0*1 + 0.5*1 + 0.6 = 1.1
= 0*1 + 0.5*1 + 0.6 = 1.1 ![]() = 1*1 + 0*1 + 0.4 = 1.4
= 1*1 + 0*1 + 0.4 = 1.4
所以,![]() ={1.1,14}
={1.1,14}
(2)![]()
![]() = 0*2 + 0.5*3 + 0.6 = 2.1
= 0*2 + 0.5*3 + 0.6 = 2.1 ![]() = 1*2 + 0*3 + 0.4 = 2.4
= 1*2 + 0*3 + 0.4 = 2.4
所以,![]() ={2.1,2.4}
={2.1,2.4}
四舍五入方式,![]() = {1,1}还是可以对应上输入,但是
= {1,1}还是可以对应上输入,但是![]() = {2,2},显然
= {2,2},显然![]() 与
与![]() 重叠了。
重叠了。
那么在![]() 、
、![]() ,同理,只要我们的{x,y}的坐标只要在x∈{1.5,2},y∈{2.0,2.4}之间的梯度都是0,所以网络是不可微分的,导致网络无法反向传播。
,同理,只要我们的{x,y}的坐标只要在x∈{1.5,2},y∈{2.0,2.4}之间的梯度都是0,所以网络是不可微分的,导致网络无法反向传播。
S操作中,为了避免上述问题,使用如下公式解决:
其中,![]() 表示输出的通道为c的Feature Map,
表示输出的通道为c的Feature Map,![]() 表示输入通道为c的(n,m)位置的值,k表示采样核,
表示输入通道为c的(n,m)位置的值,k表示采样核,![]() 和
和![]() 表示k的参数,(n,m)表示U中要计算数值的位置。
表示k的参数,(n,m)表示U中要计算数值的位置。
在图像处理中,我们通常使用双线性插值解决输入输出的映射关系,论文也是这么做的,那么,将公式(3)使用双线性插值,如下公式:
公式看起来是不是很费劲,举个例子说明一下吧^_^,还拿上面![]() 的例子,请看下图:
的例子,请看下图:
输出层Layer I的![]() ={1.6,2.4},为了计算
={1.6,2.4},为了计算![]() ,将输入值带入公式(5),得:
,将输入值带入公式(5),得:
V = ![]() *(1 - |1.6-1|)*(1 - |2.4 - 2|) +
*(1 - |1.6-1|)*(1 - |2.4 - 2|) + ![]() *(1 - |1.6 - 1|)*(1 - |2.4 - 3|) +
*(1 - |1.6 - 1|)*(1 - |2.4 - 3|) + ![]() (1 - |1.6 - 2|)*(1 - |2.4 - 2|) +
(1 - |1.6 - 2|)*(1 - |2.4 - 2|) + ![]() *(1 - |1.6 - 2|) * (1 - |2.4 - 3|)
*(1 - |1.6 - 2|) * (1 - |2.4 - 3|)
=![]() *(1 - 0.6)*(1 - 0.4) +
*(1 - 0.6)*(1 - 0.4) + ![]() *(1 - 0.6)*(1 - 0.6) +
*(1 - 0.6)*(1 - 0.6) + ![]() (1 -0.4)*(1 -0.4) +
(1 -0.4)*(1 -0.4) + ![]() *(1 - 0.4) * (1 - 0.6)
*(1 - 0.4) * (1 - 0.6)
从之前的公式:
就可以看出来,只有参数或者输入特征值变化,就会因为输出对应Feature的值的变化,这样可以利用梯度下降更新参数达到最优解。
STN(Spatial Transformer Networks)总结
再回顾一下ST模块的结构图:
ST模块可以方便的嵌入到CNN网络中,利用非线性差值将输入U和输出V进行仿射变换得到映射关系,从而利用网络反向传播优化参数,达到数据在空间位置上的最优值。
STN效果
我们已经了解STN的原理及使用方法,最后我们看一下STN的实验效果,首先看一下在MNIST数据上的效果:
经过ST模块之后将有效数据放大居中,增加网络识别效果。
下面是论文中的门牌识别效果:
门牌数字识别中,每张图有1-5个门牌数字,每个数字输出为11维数据,0~10维代表数字0-9,11维代表没有数字。从实验结果可以看出,带ST模块的CNN网络错误率都低于其他网络,并且在使用多ST模块的网络中速度仅仅比不带ST的CNN满了6%。
论文中的鸟类识别效果:
鸟类识别中,每步使用了两个ST模块,分别提取了鸟类的不同位置(头部和身体)再进行识别。从实验结果可以看出来到ST的CNN效果都优于没有ST的CNN。
以上就是STN模型的分享,利用空间变化上实现了空间注意力的效果,从而提升了CNN的识别效果。有疑问或者愿意交流的同学可以留言。觉得文章还不错的同学,希望点个赞,求个关注,谢谢支持^_^。下一篇分享CBAM注意力机制。