ICCV2023｜DSConv：用于管状结构分割的动态蛇形卷积

题目：Dynamic Snake Convolution based on Topological Geometric Constraints for Tubular Structure Segmentation
论文：https://arxiv.org/abs/2307.08388
代码：https://github.com/YaoleiQi/DSCNet（代码会在未来的四周内全部更新完毕）
审稿：Accepted by ICCV 2023
联系: [email protected]

简介

管状结构（例如血管、道路）是临床、自然界等各领域场景中十分重要的一种结构，其的精确分割可以保证下游任务的准确性与效率。然而这并不是一个简单的任务，主要的挑战源于细长微弱的局部结构特征与复杂多变的全局形态特征。本文关注到管状结构细长连续的特点，并利用这一信息在神经网络以下三个阶段同时增强感知：特征提取、特征融合和损失约束。分别设计了动态蛇形卷积（Dynamic Snake Convolution），多视角特征融合策略与连续性拓扑约束损失。我们同时给出了基于2D和3D的方法设计，通过实验证明了本文所提出的DSCNet在管状结构分割任务上提供了更好的精度和连续性。

思考

在开始介绍工作之前，我想和读者讨论下在大模型时代下，专用分割方法的价值。

随着SAM（Segment Anything）[1]、Universal Model [2] 等一众非常优秀的分割基础模型的提出，越来越多的分割目标只需要在大模型的基础上，直接测试或简单微调，就能够得到让人十分满意的结果。这不免让人感到迷茫，继续做专用分割工作是否还有价值？后续的研究方向是否是要去拼大模型？或者站在前人的肩膀上去研究如何将大模型微调到专用领域？

值得注意的是，仍存在一些复杂的领域，大模型还未能够很好的覆盖（也许只是时间问题）。例如伪装目标、非显著性目标，以及本文所关注的特殊管状结构（占比小、特征弱且分布广）等等。同时，当分割的对象上升到3D乃至4D的数据时，一些复杂的结构（3D的血管、气管等）也困扰着大模型。当然，一些特殊的场景，需要非常高的精度，例如临床，1%的误差对于诊断都有着非常大的危险。

因此，将专用模型与大模型相结合，会促进研究发展地更快、更好。大模型关注更多的是普适性，通用性和便捷性，在此基础上，大模型针对性地补充领域专有的特征信息，能够更加快捷地获得更高的精度。

挑战

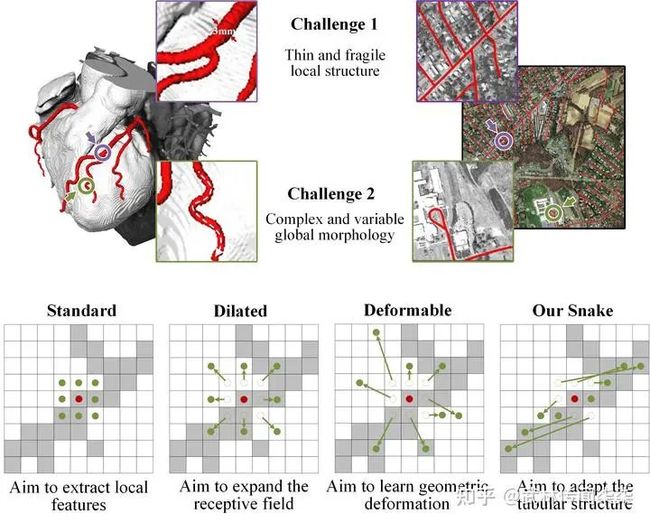
图1. 上图：显示了三维心脏血管数据集和二维遥感道路数据集，这两个数据集都旨在提取管状结构，但由于脆弱的局部结构和复杂的全球形态，这项任务存在很多挑战。下图：标准卷积核旨在提取局部特征。在此基础上，可变形卷积核丰富其应用，并适应不同目标的几何形态，但针对细长的管状结构容易丢失关注

管状结构的精确提取仍然具有挑战：

细长且脆弱的局部结构。如图1所示，细长的结构仅占整个图像的一小部分，像素的组成有限。此外，这些结构容易受到复杂背景的干扰，因此模型很难精确分辨目标的细微变化，从而导致分割出现破碎与断裂。

复杂且多变的全局形态。图1显示了细长管状结构复杂多变的形态，即使在同一张图像中也是如此。位于不同区域的目标的形态变化取决于分支的数量、分叉的位置，路径长度以及其在图像中的位置。因此当数据表现出未曾见过的形态特征时，模型倾向于过拟合到已见过的特征，无法识别未见过的特征形态，从而导致泛化性较弱。

动机

受到Deformable Convolution[3]的启发，我们希望模型在学习特征的过程中，改变卷积核的形状，从而关注管状结构的核心结构特点。由此衍生出很多工作[4] [5]，并在视网膜血管的分割工作中得到了应用。然而在我们的初期实验中发现，由于管状结构所占比例较小，模型不可避免地失去对相应结构的感知，卷积核完全游离在目标以外。因此我们希望根据管状结构的特点来设计特定的网络结构，从而指导模型关注关键特征。

方法

图2. 完整框架图

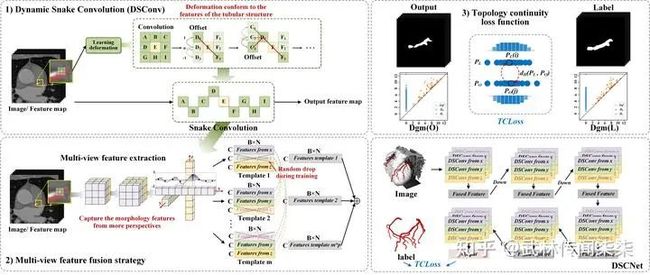
动态蛇形卷积核（Dynamic Snake Convolution, DSConv）

我们希望卷积核一方面能够自由地贴合结构学习特征，另一方面能够在约束条件下不偏离目标结构太远。在观察管状结构的细长连续的特征后，脑海里想到了一个动物——蛇。我们希望卷积核能够像蛇一样动态地扭动，来贴合目标的结构。

我们观察一下形变卷积的操作核心[3]：

图3. 可形变卷积中的偏置学习

我们会发现，操控单个卷积核形变的所有偏置(offset)，是在网络中一次性全部学到的，并且阅读其核心代码会发现，对于这一个偏置只有一个范围的约束，即感受野范围(extend)。控制所有的卷积发生形变，是依赖于整个网络最终的损失约束回传，这个变化过程是相当自由的。

图4. 左图：DSConv坐标的计算方法。右图：DSConv的真实感受范围

完全的自由，容易让模型丢失占比小的细小结构特征，这对于细长管状结构分割任务来说，是一个巨大挑战。因此，如图4所示，我们以蛇来举例，蛇的连续移动，是其头带动身体，一节一节如同波浪一般。因此，我们将连续性约束加入卷积核的设计中。每一个卷积位置都由其前一个位置作为基准，自由选择摆动方向，从而在自由选择的同时确保感受的连续性。（具体的公式可以参考论文与代码）

这样的设计是否真的有用？我们进行了可视化验证：

图5. 我们在每张图像上叠加3层的卷积核位置，共计729个点（红色），以显示给定点（黄色）的卷积核的位置和形状。底部：热图显示了每个卷积的感兴趣区域。

以2D的视网膜数据为例，无论血管的走向、粗细等，我们的蛇形卷积核确实能够更好地自适应到管状结构的细长结构，并且关注到核心特征。

多视角特征融合

图6. 多视角特征融合策略

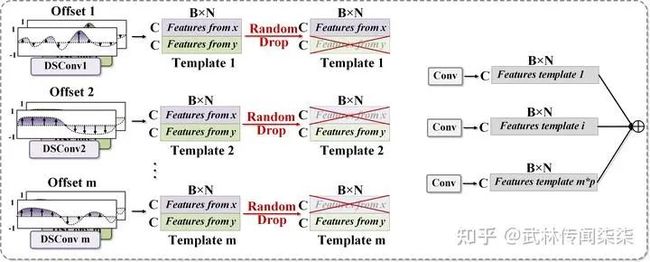
我们考虑到管状结构的走向与视角从来不是单一的，因此在设计中融合多视角特征也是必然的选择。然而，融合更多的特征带来的必然结果，就是更大的网络负载，且如此多的特征难免会出现冗余，因此我们在特征融合的训练过程中加入了分组与随机丢弃的策略，一定程度上缓解了网络内内存的压力并避免模型陷入过拟合。

基于持续同调的拓扑连续损失（TCLoss）

图7. 基于持续同调的连续性拓扑约束

我们的目标是构建数据的拓扑结构，并提取复杂管状结构中的高维关系，也就是持续同源性（Persistence Homology, PH）。基于PH所设计的拓扑损失函数也有很多优秀的工作[6] [7]已经采用，拓扑约束确实针对这类细长且占比小的结构非常有效，设计中所采用的推土机距离（Wasserstein Distance, WD）用来衡量点集的差异。简单描述，WD用来衡量的是从一种离散分布，转变为另一种离散分布需要的代价。在[6] [7]的方法中，利用这一算法来计算点与点的最佳匹配，点集中的离散点会被匹配到对角线（刚出现就消失的点聚集在对角线上），因此这些离散的点不会参与损失函数的计算与约束。

假设PO的上端存在着一个异常的离散点（横坐标表示出现的时间，纵坐标表示消失的时间），这表明存在一个构件直到最后才与其他构件获得连接从而消失。因此我们在本文中采用的是豪斯多夫距离（Hausdorff Distance, HD），HD也是用于衡量点集相似度的一个重要算法，对离散点也非常敏感。

实验

文中，我们使用了三个数据集，包含两个公共数据集和一个内部数据来验证我们的方法。在2D中，我们评估了DRIVE视网膜数据集和Massachusetts Roads数据集。在3D中，我们使用了一个名为心脏CCTA数据的数据集（私有数据）。后续，我们也在3D KIPA公开数据上做了验证，并且正在致力于用该方法测试多组公开挑战赛数据集，实验结果会在后续逐步公布。

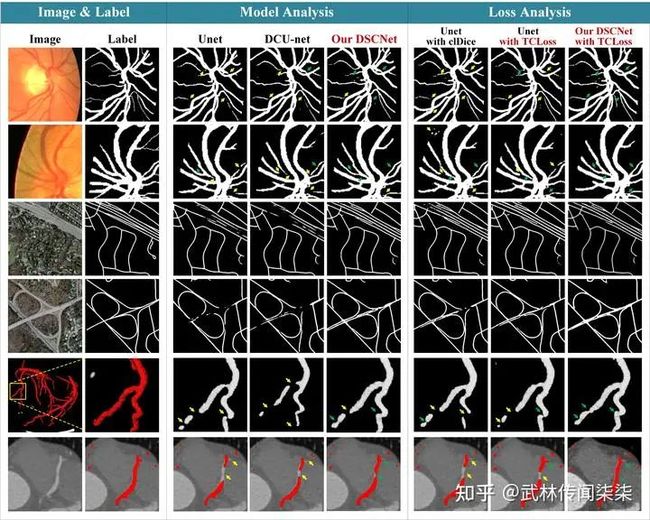
图8. 可视化结果

从可视化结果可以发现，我们的方法确实对管状结构数据有着很好的分割效果，尤其是在遥感道路数据以及冠脉血管数据上。

图9. 量化结果

总结

我们提出的框架针对细长管状结构进行了相应设计，并成功地将形态学特征与拓扑学知识融为一体，以共同指导模型自适应的分割。然而，其他形态学结构的目标是否也有类似的范式，并能够通过这一方法获得更好的性能仍然是一个有趣的话题。同时，我们也正在尝试将其进一步优化，能够作为基础大模型中的一个通用框架，为这类特征难以鉴别的结构提供一种可行的范式。