纳什均衡

纳什均衡

如果对于所有参与人$i$有$$u_i({\sigma }_i^{\ast },{\sigma }_{-i}^{\ast })\ge u_i(s_i,{\sigma }_{-i}^{\ast })(s_i\in S_i)$$那么混合策略组合${\sigma }^{\ast }$是一种纳什均衡

严格纳什均衡

如果对于所有参与人$i$有$$u_i(s_i^{\ast },s_{-i}^{\ast })\ge u_i(s_i,s_{-i}^{\ast })(s_i\in S_i)$$等号成立当且仅当$s_i=s_i^{\ast }$
那么纯策略组合${\sigma }^{\ast }$是一种严格纳什均衡

纳什均衡计算方法

例1. 考虑以下鹰兔博弈，求所有纳什均衡

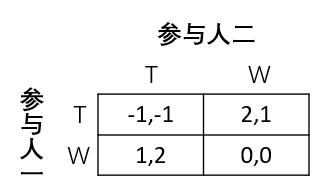
纳什均衡的意义在于利益最大化，所以仅需将利益最大化时策略间的关系求出即可
令$x={\sigma }_1(T),y={\sigma }_2(T)$，则${\sigma }_1(W)=1-x,{\sigma }_2(W)=1-y$，效用为$$u_1({\sigma }_1)=-xy+2x(1-y)+(1-x)y=x(2-4y)+y$$对于$y<\frac{1}{2}$，$x=1$；对于$y>\frac{1}{2}$，$x=0$；对于$y=\frac{1}{2}$，$x\in [0,1]$ $$x=\{\begin{array}{ll}1,& 0\le y<\frac{1}{2}\\ 0,& \frac{1}{2}<y\le 1\\ x\in [0,1],& y=\frac{1}{2}\end{array}$$
同理得到参与人二的利益最大函数$$y=\{\begin{array}{ll}1,& 0\le x<\frac{1}{2}\\ 0,& \frac{1}{2}<x\le 1\\ y\in [0,1],& x=\frac{1}{2}\end{array}$$
将两个函数绘制在一个坐标系中

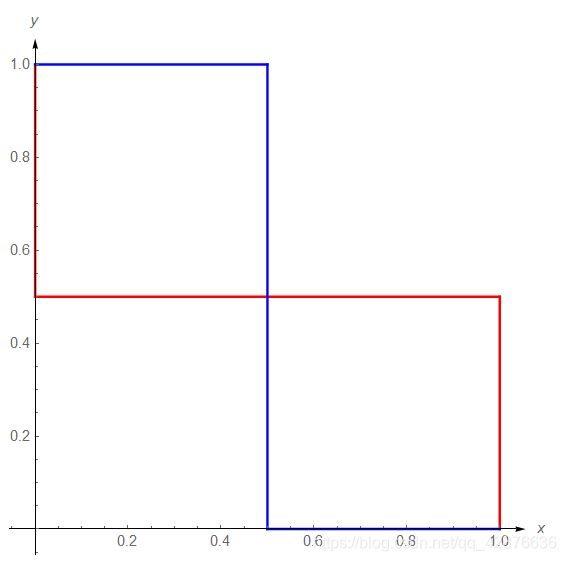
红色曲线为参与人一利益最大曲线，蓝色为参与人二利益最大曲线
不难看出有三个点两个参与人利益均最大，即$(0,1),(1,0),(\frac{1}{2},\frac{1}{2})$
故此三个点对应的策略组合即为纳什均衡

例2. 在某地有两个产商垄断市场，分别生产$q_1,q_2$的商品。若市场价格与总产量$q=q_1+q_2$的关系为$p(q)$，第$i$个厂商生产的单位成本为$c_i(q_i)$，每个产商会根据对方的产量调整自己的产量以是自己的利益最大化，$p(q)=1-q$，$c_i(q_i)=c{q}_i$（$c$为常数），求两个产商最终稳定的产量（即求纳什均衡）

第$i$个的厂商的利润为$u_i=q_{i}p(q)-c_i(q_i)$，由于利益最大，则$$\frac{\partial u_i}{\partial q_i}=q_i{p}^{\prime }(q)+p(q)-c_i^{\prime }(q)=0$$代入$p(q)=1-q,c_i(q_i)=c{q}_i$得到$-q_i+1-q-c=0$，即$q+q_i=1-c$，则$$\{\begin{array}{l}2q_1+q_2=1-c\\ q_1+2q_2=1-c\end{array}$$解得$$\{\begin{array}{l}{q}_1=\frac{1-c}{3}\\ q_2=\frac{1-c}{3}\end{array}$$

结合例题不难看出，纳什均衡的求解方法就是找出利益最大曲线，然后解出交点