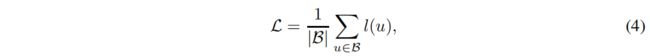【论文阅读】GraphCL:Contrastive Self-Supervised Learning of Graph Representations
图表示的对比自监督学习
- 摘要
- 1 引言
- 2 方法
-
- 2.1 背景情况
- 2.2 GraphCL
- 2.3 GraphCL概述
- 3 实验
摘要
本文提出了图对比学习(GraphCL),一个以自监督方式学习节点表示的一般框架。GraphCL 通过最大化同一节点局部子图的内在特征和链接结构的两个随机扰动版本的表示之间的相似性来学习节点嵌入。我们使用GNN生成同一节点的两种表示,并利用对比学习损失来最大化它们之间的一致性。在transductive和inductive学习设置中,我们证明了我们的方法在许多节点分类基准上显著优于最新的无监督学习。
1 引言
图表示学习面临的主要挑战之一是学习同时捕获节点特征和图结构的节点嵌入。
为了弥补标签或预定义任务的缺失,部分无监督方法采用了同质性假设,即相连节点应该在嵌入空间中相邻。受将单词嵌入潜在空间的Skipgram算法(相邻向量对应于句子中的共同出现的单词)的启发,这些方法中的大多数使用随机游动生成类似句子的序列,其中共同出现的节点在嵌入空间中很近。其他方法,如autoencoders,也通过重建邻接矩阵或节点的邻域来使用上述同质性假设。尽管这些方法在学习表示方面取得了成功,但基于同质性假设,这些方法偏向于强调节点的直接邻近拓扑信息。DGI的成功归因于输入的全局和局部部分之间的互信息最大化。这需要学习整个图的全局表示,这在处理大型图时可能非常昂贵,甚至难以处理。
本文引入了GraphCL,一个通用的对比学习框架,它通过最大化同一节点局部子图的两个随机扰动版本的表示之间的相似性来学习节点嵌入。除了学习对图的随机扰动具有鲁棒性的节点表示外,GraphCL还允许有效的自监督学习节点表示。
GraphCL的灵感来自于最近一种方法的成功,该方法利用对比学习损失来学习视觉表征,从而在同一图像的多个视图中捕获共享信息。这些方法基于这样的假设,即重要信息在不同的视图之间共享。有的论文使用数据增强技术生成同一图像的多个视图,而有的则将图像的不同通道视作不同的视图。
在GraphCL中,对于每个节点,随机扰动都应用于它的 L − h o p L-hop L−hop 子图。该扰动包括随机dropout边的一个子集和节点的 L − h o p L-hop L−hop 子图的内在特征。dropout概率是超参数。
2 方法
2.1 背景情况
(1)公式定义
G = ( V , E ) \mathcal{G}=(\mathcal{V},\mathcal{E}) G=(V,E)是一个无向图,其中 V \mathcal{V} V是节点集, E ⊆ V × V \mathcal{E} ⊆\mathcal{V}×\mathcal{V} E⊆V×V是边集。每个节点 u ∈ V u∈\mathcal{V} u∈V由一个特征向量 x u ∈ R P x_u∈\mathbb{R}^P xu∈RP表示。邻接矩阵 A ∈ R N × N A∈\mathbb{R}^{N×N} A∈RN×N表示图的拓扑结构,其中 N = ∣ V ∣ N=|\mathcal{V}| N=∣V∣是图中的节点数。在不失一般性的情况下,我们假设图是不加权的,即如果 ( u , v ) ∈ E (u,v)∈\mathcal{E} (u,v)∈E,则 A u , v = 1 A_{u,v}=1 Au,v=1,否则 A u , v = 0 A_{u,v}=0 Au,v=0。我们还提供了节点特征集,即 X = { x 1 , x 2 , . . . , x N } X=\{x_1,x_2,...,x_N\} X={x1,x2,...,xN}。
设 G u = ( V u , E u ) \mathcal{G}_u=(\mathcal{V}_u,\mathcal{E}_u) Gu=(Vu,Eu)是以节点 u u u为中心的 L − h o p L-hop L−hop 子图, X u = { x j } j ∈ V u X_u=\{x_j\}_{j∈\mathcal{V}_u} Xu={xj}j∈Vu是与 u u u的邻域子图中的节点相对应的特征向量集。 u u u子图中的关系信息由其对应的邻接矩阵 A u A_u Au表示。我们的目标是学习节点的表示。这将通过学习一个GNN编码器 f f f来实现,该编码器将节点级信息和图结构映射到更高阶的表示,即对于每个 u ∈ V u∈\mathcal{V} u∈V, f ( X u , A u ) = h u ( L ) ∈ R P ′ f(X_u,A_u)=h_u^{(L)}∈\mathbb{R}^{P'} f(Xu,Au)=hu(L)∈RP′,其中 P ′ P' P′为嵌入大小。值得指出的是,嵌入 h u ( L ) h_u^{(L)} hu(L)对应于GNN的第 L L L层的输出,它涉及到节点 u u u的 L − h o p L-hop L−hop 子图中的节点。在本文的其余部分中, h u h_u hu指的是GNN最后一层的输出,即 h u = h u ( L ) h_u=h_u^{(L)} hu=hu(L)。
(2)GNNs
GNNs是一种图嵌入架构,它除了使用节点和边特征外,还使用图结构为每个节点生成一个表示向量(即嵌入)。最近的GNNs通过聚合相邻节点和边的特征来学习节点表示。这些GNNs的第 l l l层的输出通常表示为:
![]()
其中, h u ( l ) h_u^{(l)} hu(l)是由 h u ( 0 ) = x u h_u^{(0)}=x_u hu(0)=xu初始化的第 l l l层的节点 u u u的特征向量, N ( u ) \mathcal{N}(u) N(u)是节点 u u u的一阶邻域的集合。不同的GNNs使用不同的COMBINE(组合)和AGGREGATE(聚合)函数;本文使用的将在下一节中描述。
2.2 GraphCL

GraphCL框架有三个主要组成部分:随机扰动、基于GNN的编码器和对比损失函数。我们首先介绍每个组件,然后给出该方法的高级概述。
- (1)随机扰动:我们将随机扰动应用于以每个节点为中心的 L − h o p L-hop L−hop 子图,从而得到两个邻域子图,它允许我们获得同一节点的两个表示,我们将其看作正例。在这项工作中,我们考虑节点特征和子图连通性的同时变换。子图结构通过使用来自伯努利分布的样本以概率 p p p随机丢弃边来转换。对于节点的内在特征,我们应用了类似的策略,即仅将dropout应用到输入特征中;如图1所示。
- (2)GNN编码器:我们应用了一个基于GNN的编码器来学习与每个节点 u u u相关联的两个转换后的 L − h o p L-hop L−hop 子图的表示。我们的框架支持GNN的多种选择。我们选择 mean-pooling 传播规则作为主要构件,并对 inductive和transductive设置采取了不同的选择。
- (3)对比损失函数:我们定义了一个pretext预测任务,其目的是在给定一组生成的示例的情况下,识别表示 h u , 1 h_{u,1} hu,1的相应正示例 h u , 2 h_{u,2} hu,2,其中 h u , 1 h_{u,1} hu,1和 h u , 2 h_{u,2} hu,2是一对正示例(即,从同一节点周围 L − h o p L-hop L−hop 子图的两个变换的GNN表示中获得)。
我们随机采样一个包含 M M M个节点的minibatch B \mathcal{B} B,并定义它们相应的 L − h o p L-hop L−hop 子图。我们对每个节点的子图应用2个变换,从而得到 2 M 2M 2M个子图,使我们能够得到用于对比预测任务的正表示对。与明确采样负例相反,我们将minibatch中的其他 ( 2 M − 2 ) (2M-2) (2M−2)【 ( M − 1 ) × 2 (M-1)×2 (M−1)×2】个例子视为负例。
对于minibatch中的每个节点 u u u,我们计算以下损失函数,它基于一个归一化的温度尺度交叉熵(a normalized temperature-scaled cross entropy):
![]()
其中, l i , j ( u ) l_{i,j}(u) li,j(u)被定义为:

其中, s ( h u , i , h u , j ) = h u , i T h u , j / ∣ ∣ h u , i ∣ ∣ ∣ ∣ h u , j ∣ ∣ s(h_{u,i},h_{u,j})=h^T_{u,i}h_{u,j}/||h_{u,i}|| ||h_{u,j}|| s(hu,i,hu,j)=hu,iThu,j/∣∣hu,i∣∣∣∣hu,j∣∣是两个表示 h u , i h_{u,i} hu,i和 h u , j h_{u,j} hu,j之间的余弦相似度, 1 [ u ≠ v ] \mathbb{1}_{[u≠v]} 1[u=v]是一个指示器函数,当 u ≠ v u≠v u=v时等于 1 1 1, τ τ τ是一个温度参数。【分母是 ( M − 1 ) (M-1) (M−1)个负例】
2.3 GraphCL概述
对于每个取样的minibatch B \mathcal{B} B,我们应用以下步骤:
- 对于minibatch中的每个节点 u u u,我们将 ( X u , A u ) (X_u,A_u) (Xu,Au)定义为子图,其中包含图中最多距离 u u u L − h o p s L-hops L−hops 的所有节点和边及其相应的特征;
- 绘制两个随机扰动 t 1 t_1 t1和 t 2 t_2 t2,并将它们应用于 u u u的 L − h o p L-hop L−hop 邻域子图:
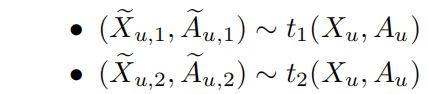
- 利用编码器得到节点 u u u的两个表示:

- 使用下列损失函数更新编码器 f f f: