【二叉树的链式结构（二叉链）及实现】
二叉树的链式结构
在看二叉树基本操作前，再回顾下二叉树的概念，二叉树是：
1. 空树
2. 非空：根节点，根节点的左子树、根节点的右子树组成的。
（注意： 到这里就不再有左右孩子结点的概念，因为要应用递归思想，因此只有根节点、左子树、右子树的概念 ）
从概念中可以看出，二叉树定义是递归式的，因此后序基本操作中基本都是按照该概念实现的。
- 这里需要注意的是链式二叉树基于其特殊的物理结构，我们不像实现其它数据结构时去实现它的增删查改，因为比起这些操作，二叉树更有价值的是它特殊的递归结构 ，因此我们所研究的是如何去利用其递归结构，二叉树的增删查改一定程度上是无意义的，当然后续一些特殊的二叉树，如搜索二叉树等，增删查改才有意义，但不在我们当前研究范围内，因此这种特殊情况就先不考虑。
链式二叉树的实现
前置说明
在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。由于现在我们对二叉树结构掌握还不够深入，为了降低学习成本，此处可以手动快速创建一棵简单的二叉树，快速进入二叉树操作学习，等二叉树结构了解的差不多时，反过头再来研究二叉树真正的创建方式，创建方式如下：
//首先要定义表示结点的结构体
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
//其次要写一个构建结点的函数
BTNode* BuyNode(BTDataType x)
{
BTNode* node =(BTNode*) malloc(sizeof(BTNode));
if (node == NULL)
{
perror("malloc fail");
exit(-1);
}
node->data = x;
node->left = NULL;
node->right = NULL;
return node;
}
//最后构建二叉树，先造结点，后链接结点
BTNode* CreatBinaryTree()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}
int main()
{
BTNode* BTtree = CreatBinaryTree();
return 0;
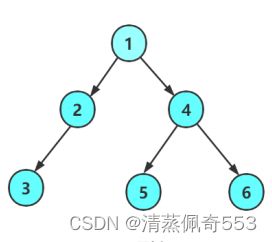
}根据以上代码造的二叉树图示如下：
注意：上述代码并不是创建二叉树的方式，真正创建二叉树方式后序详解重点讲解。
有了二叉树， 我们就可以来实现链式二叉树相关操作的各个接口：
二叉树的遍历
前序、中序以及后序遍历
学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。
按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：
1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问顺序为：根节点->左子树->右子树。
2. 中序遍历(Inorder Traversal)——访问顺序为：根节点->左子树->右子树
3. 后序遍历(Postorder Traversal)——访问顺序为：根节点->左子树->右子树
由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
（为了学习二叉树结构的精华，当更节点无子树时，就称其左右子树为空，用空指针NULL表示）
下面通过一个示例来加深理解
根据以上结构，我们很容易看出不同遍历时的访问情况，据此我们就可用递归的方式来分别实现三种遍历 。
// 二叉树前序遍历
void PreOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%d ", root->data);
PreOrder(root->left);
PreOrder(root->right);
}
// 二叉树中序遍历
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}
// 二叉树后序遍历
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
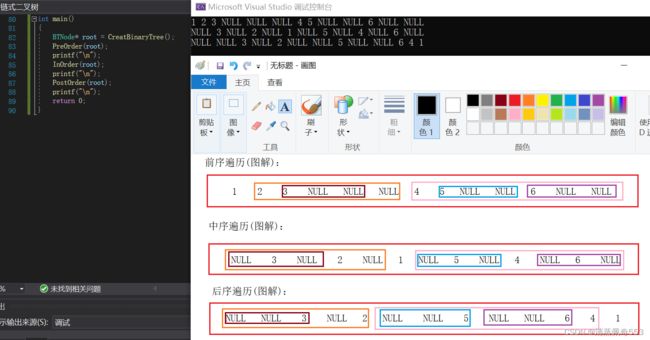
}运行测试结果如下，与之前分析结果一致，即为正确：
层序遍历
除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。
为了实现层序遍历，我们需要用到队列这一数据结构，具体实现过程图解如下：
代码如下（因为需要用到队列，故要把我们之前写过的queue.h和queue.c两个文件拷贝到此工程中）：
//二叉树层序遍历
int BinaryTreeSize(BTNode* root);
void LevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q,root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
printf("%d", front->data);
QueuePop(&q);
if (front->left)
QueuePush(&q, front->left);
if (front->right)
QueuePush(&q, front->right);
}
printf("\n");
QueueDestroy(&q);
}注意以下几点：
1.结点入队列的时候，我们只需要将结点的地址存进去即可，因此我们在queue.h中要把Queuedatatype的类型定位BTNode*,此时还要把定义BTNode这一结构体移到queue.h中定义队列结点之前，否则找不到BTNode*这一类型
2.记得初始化队列以及销毁队列
测试结果如下，即为成功：
二叉树的相关计算
求二叉树节点个数
二叉树求总结点数用递归子问题的角度来分析，可以看做左子树结点数+右子树节点数+1,当根节点为NULL时，返回0，代码如下：
// 二叉树节点个数 int BinaryTreeSize(BTNode* root) { if (root == NULL) return 0; int leftnode = BinaryTreeSize(root->left); int rightnode = BinaryTreeSize(root->right); return leftnode + rightnode + 1; }递归分析图示：
还有更加简洁的写法写成下列写法(三目操作符)：
// 二叉树节点个数 int BinaryTreeSize(BTNode* root) { return root==NULL?0:BinaryTreeSize(root->left)+BinaryTreeSize(root->right)+1; }
求二叉树叶子节点个数
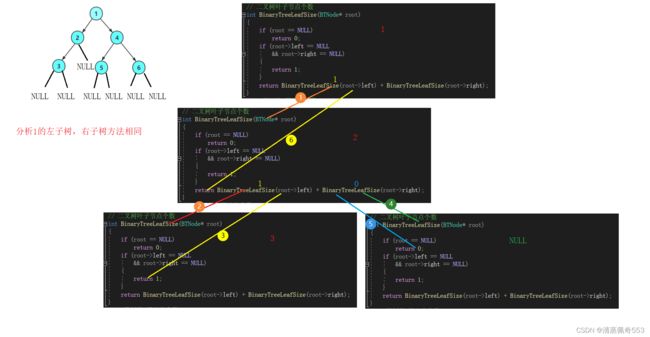
求叶子结点个数同样可以用递归的思想来看，可以看做左子树的叶子结点数+右子树的叶子节点数，根节点为NULL时，返回0，当根节点的左子树和右子树为空时，说明该节点是叶子结点返回，代码如下：
// 二叉树叶子节点个数 int BinaryTreeLeafSize(BTNode* root) { if (root == NULL) return 0; if (root->left == NULL && root->right == NULL) { return 1; } return BinaryTreeLeafSize(root->left)+BinaryTreeLeafSize(root->right); }递归分析图示：
求二叉树第k层的结点个数
从递归子问题的角度，求第k层节点个数可以想成左子树的第k-1层节点个数+右子树第k-1层节点个数，根节点为NULL时返回0，当k=1时,说明此时求的是这颗树的第一层，而二叉树的第一层节点个数是1，返回1,代码如下：
int BinaryTreeLevelKSize(BTNode* root, int k) { if (root == NULL) return 0; if (k==1) return 1; return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1); }递归分析图示：
二叉树查找值为x的节点
从递归子问题角度来考虑，相当于根节点的值与所给值比较，相等就直接返回该节点地址，不相等就看该节点左右子树的根节点的值是否与所给值相等，若相等，返回对应的根节点，若没有相等，则返回空指针，若根节点本身为空也直接返回空指针，代码如下：
// 二叉树查找值为x的节点 BTNode* BinaryTreeFind(BTNode* root, BTDataType x) { if (root == NULL) return NULL; if (root->data == x) return root; struct BinaryTreeNode* ret1 = BinaryTreeFind(root->left, x); if (ret1) return ret1; struct BinaryTreeNode* ret2 = BinaryTreeFind(root->left, x); if (ret2) return ret2; //if (BinaryTreeFind(root->left, x)) // return BinaryTreeFind(root->left, x); //if(BinaryTreeFind(root->right, x)) // BinaryTreeFind(root->right, x); return NULL; }递归过程都和前三个大同小异，可以根据需求自己尝试画图
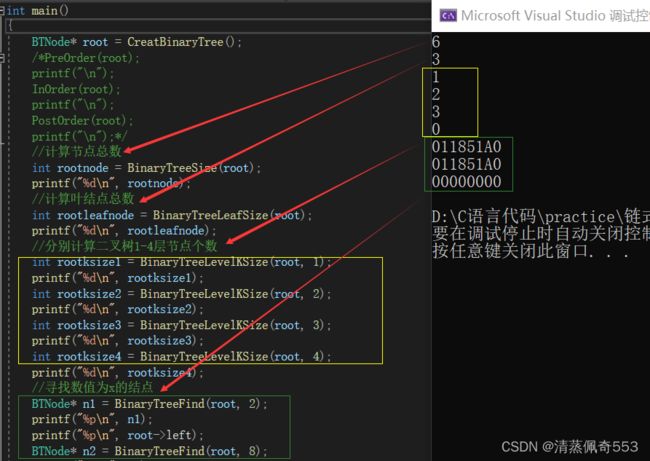
测试以上四段代码，若结果如下，则为正确：
二叉树的创建和销毁
二叉树的创建：
我们基于一道OJ题来解决此问题：
根据我们之前学习前序遍历的遍历特点，我们可以画出如下树形结构：
代码如下，测试通过，说明代码正确：
#include
#include
//创建表示树结点的结构体
struct TreeNode
{
char data;
struct TreeNode*left;
struct TreeNode*right;
};
//前序遍历数组创建二叉树
struct TreeNode* RebuildTree(char*str,int* pi)//接收i的地址，就能达到改变主函数中i值的效果
{
//是‘#’就返回空
if(str[*pi]=='#')//不能写成str[(*pi)++]=='#'，因为这样就算不等于‘#’，下标也会+1
{
(*pi)++;//不要忘记是‘#’也要存到数组里
return NULL;
}
//不是‘#’，就创建新结点
struct TreeNode*root=(struct TreeNode*)malloc(sizeof(struct TreeNode));
root->data=str[(*pi)++];//创建好的新结点的值就可以存到数组里，同样要让下标++
root->left=RebuildTree(str,pi);//读取到的下一个值就直接链接到当前节点的左边，开始递归
root->right=RebuildTree(str,pi);//左边递归回来后的下一个值就直接链接到当前节点的右边
return root;
}
//中序遍历
void InOrder(struct TreeNode* root)
{
if (root == NULL)
{
return;
}
InOrder(root->left);
printf("%c ", root->data);
InOrder(root->right);
}
int main() {
char str[100]={0};//根据题目要求创建一个能容纳100个字符串的数组
while(scanf("%s",str)!=EOF)//根据题目要求，能输入多组测试用例
{
int i=0;
struct TreeNode*ret= RebuildTree(str,&i);//用一个值接收创建好的树的根节点
InOrder(ret);//对创建好的树进行中序遍历
}
return 0;
} 二叉树的销毁：
销毁二叉树我们要用到后序遍历的思想，即要先销毁左子树再消除右子树最后销毁根，因为如果把根先销毁了，就找不到左右子树了，代码如下：
//销毁二叉树
void BinaryTreeDestory(BTNode* root)
{
if (root != NULL)
{
BinaryTreeDestory(root->left);
BinaryTreeDestory(root->right);
free(root);
root = NULL;
}
}判断二叉树是否是完全二叉树：
//判断是否为完全二叉树
bool TreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q,root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front == NULL)
{
break;
}
else
{
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front != NULL)
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}链式二叉树应用（OJ练习）：题目均来源于leetcode，均附有链接
单值二叉树
力扣
如果二叉树每个节点都具有相同的值，那么该二叉树就是单值二叉树。只有给定的树是单值二叉树时，才返回
true；否则返回false。
bool isUnivalTree(struct TreeNode* root){
if(root==NULL)
return true;
if(root->left&&root->left->val!=root->val)
return false;
if(root->right&&root->right->val!=root->val)
return false;
return isUnivalTree(root->left)&&isUnivalTree(root->right);
}检查两棵树是否相等
力扣
给你两棵二叉树的根节点
p和q，编写一个函数来检验这两棵树是否相同。如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
if(p==NULL&&q==NULL)
return true;
if(p==NULL||q==NULL)
return false;
if(p->val!=q->val)
return false;
return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}判断一个树是否为另一个树的子树
力扣
https://leetcode.cn/problems/subtree-of-another-tree/
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
if(p==NULL&&q==NULL)
return true;
if(p==NULL||q==NULL)
return false;
if(p->val!=q->val)
return false;
return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
if(root==NULL)
return false;
if(isSameTree(root,subRoot))
return true;
return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
}对称二叉树
力扣https://leetcode.cn/problems/symmetric-tree/
给你一个二叉树的根节点
root， 检查它是否轴对称。
bool isSymmetric1(struct TreeNode* root1,struct TreeNode* root2)
{
if(root1==NULL&&root2==NULL)
return true;
if(root1==NULL||root2==NULL)
return false;
if(root1->val!=root2->val)
return false;
return isSymmetric1(root1->left,root2->right)&&isSymmetric1(root1->right,root2->left);
}
bool isSymmetric(struct TreeNode* root){
if(root==NULL)
return true;
struct TreeNode* root1= root->left;
struct TreeNode* root2= root->right;
return isSymmetric1(root1,root2);
}二叉树的前序遍历
力扣https://leetcode.cn/problems/binary-tree-preorder-traversal/
给你二叉树的根节点
root，返回它节点值的 前序 遍历。提示：
- 树中节点数目在范围
[0, 100]内-100 <= Node.val <= 100
void preorder(struct TreeNode* root,int* a,int* returnSize)
{
if(root==NULL)
return ;
a[(*returnSize)++]=root->val;
preorder(root->left,a,returnSize);
preorder(root->right,a,returnSize);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
int*arr=(int*)malloc(sizeof(int*)*100);
*returnSize=0;
preorder(root,arr,returnSize);
return arr;
}二叉树的中序遍历（要求同前序遍历）
力扣https://leetcode.cn/problems/binary-tree-inorder-traversal/
void inorder(struct TreeNode* root,int* a,int* returnSize)
{
if(root==NULL)
return ;
inorder(root->left,a,returnSize);
a[(*returnSize)++]=root->val;
inorder(root->right,a,returnSize);
}
int* inorderTraversal(struct TreeNode* root, int* returnSize){
int*arr=(int*)malloc(sizeof(int*)*100);
*returnSize=0;
inorder(root,arr,returnSize);
return arr;
}二叉树的后序遍历（要求同前序遍历）
力扣https://leetcode.cn/problems/binary-tree-postorder-traversal/
void postorder(struct TreeNode* root,int* a,int* returnSize)
{
if(root==NULL)
return ;
postorder(root->left,a,returnSize);
postorder(root->right,a,returnSize);
a[(*returnSize)++]=root->val;
}
int* postorderTraversal(struct TreeNode* root, int* returnSize){
int*arr=(int*)malloc(sizeof(int*)*100);
*returnSize=0;
postorder(root,arr,returnSize);
return arr;
}以上就是链式二叉树（二叉链）的实现及应用，相关全部代码见下链接，欢迎参考指正：
链式二叉树 · 王哲/practice - 码云 - 开源中国 (gitee.com)https://gitee.com/ace-zhe/practice/tree/master/%E9%93%BE%E5%BC%8F%E4%BA%8C%E5%8F%89%E6%A0%91