位1的个数,编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 ‘1‘ 的个数(也被称为汉明重量)。
题记:
编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 ‘1’ 的个数(也被称为汉明重量)。
提示:
请注意,在某些语言(如 Java)中,没有无符号整数类型。在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因为无论整数是有符号的还是无符号的,其内部的二进制表示形式都是相同的。
在 Java 中,编译器使用二进制补码记法来表示有符号整数。因此,在 示例 3 中,输入表示有符号整数 -3。
示例 1:
输入:n = 00000000000000000000000000001011
输出:3
解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 ‘1’。
示例 2:
输入:n = 00000000000000000000000010000000
输出:1
解释:输入的二进制串 00000000000000000000000010000000 中,共有一位为 ‘1’。
示例 3:
输入:n = 11111111111111111111111111111101
输出:31
解释:输入的二进制串 11111111111111111111111111111101 中,共有 31 位为 ‘1’。
提示:
- 输入必须是长度为 32 的 二进制串 。
进阶:
如果多次调用这个函数,你将如何优化你的算法?
题目来源:
作者:LeetCode
链接:https://leetcode.cn/leetbook/read/top-interview-questions-easy/xn1m0i/
来源:力扣(LeetCode)
解题方法:
java的18种写法,之前在公众号[数据结构和算法]中分为3个系列专门写过,这里就不在细写了,我把答案全部列出来,因为太多,我只给一些简单的提示,如果不懂的可以看下前面写的那3个系列,有图文分析
《364,位1的个数系列(一)》
《385,位1的个数系列(二)》
《402,位1的个数系列(三)》
或者也可以在下面留言,我来给你解答。
一:把n往右移32次,每次都和1进行与运算
public int hammingWeight(int n) {
int count = 0;
for (int i = 0; i < 32; i++) {
if (((n >>> i) & 1) == 1) {
count++;
}
}
return count;
}
二:原理和上面一样,做了一点优化
public int hammingWeight(int n) {
int count = 0;
for (int i = 0; i < 32; i++) {
if ((n & (1 << i)) != 0) {
count++;
}
}
return count;
}
转换为PHP代码为:
function hammingWeight($n) {
$count = 0;
while($n){
$count += $n & 1;
$n = $n >> 1;
}
return $count;
}
三:1每次往左移一位,再和n进行与运算
public int hammingWeight(int n) {
int count = 0;
for (int i = 0; i < 32; i++) {
if ((n & (1 << i)) != 0) {
count++;
}
}
return count;
}
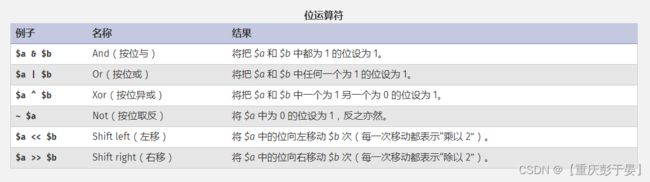
首先先来弄清楚位运算符:
位运算符
位运算符允许对整型数中指定的位进行求值和操作。
位移在 PHP
中是数学运算。向任何方向移出去的位都被丢弃。左移时右侧以零填充,符号位被移走意味着正负号不被保留。右移时左侧以符号位填充,意味着正负号被保留。要用括号确保想要的优先级。例如 $a & b = = t r u e 先进行比较再进行按位与;而 ( b == true 先进行比较再进行按位与;而 ( b==true先进行比较再进行按位与;而(a & $b) == true
则先进行按位与再进行比较。如果 &、 | 和 ^ 运算符的左右两个操作对象都是字符串,将对会组成字符串的字符 ASCII
值执行操作,结果也是一个字符串。除此之外,两个操作对象都将 转换为整数 ,结果也将会是整数。如果 ~ 运算符的操作对象是字符串,则将对组成字符串的字符 ASCII 值进行操作, 结果将会是字符串,否则操作对象和结构都会是整数。
<< 和 >> 运算符的操作对象和结果始终都是整数。
弄清楚位运算符之后再来看一下方法一的原理:
我们知道在java语言中一个int类型有32个0或1组成。我们要计算有多少个1,这里主要以int型数据为例来分析。比如15在二进制中表示的是1111,有4个1,所以返回4。再比如16在二进制中表示的是10000,只有一个1,所以返回1。这题解法比较多,我们将会逐个分析。
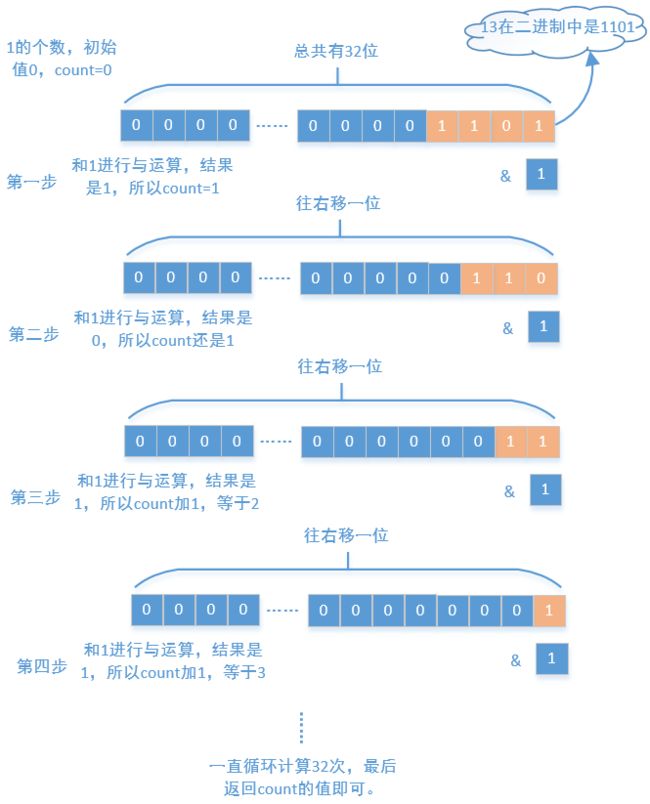
通过移动数字计算
首先想到的是把要求的数字不停的往右移,然后再和1进行与运算,我们就以13为例画个图来分析下
public int bitCount(int n) {
int count = 0;
for (int i = 0; i < 32; i++) {
if (((n >>> i) & 1) == 1) {
count++;
}
}
return count;
}
上面的分析中我们看到,如果一个数往右移了几步之后结果为0了,就没必要在计算了,所以代码我们还可以在优化一点
public int bitCount(int n) {
int count = 0;
while (n != 0) {
count += n & 1;
n = n >>> 1;
}
return count;
}
方法二的原理:
上面我们使用的是把一个数字不断的往右移动,其实我们还可以保持原数字不变,用1和他进行与运算,然后通过移动1的位置来计算,这里我们判断的标准不是等于1,而是不等于0。我们还以13为例来画个图分析一下
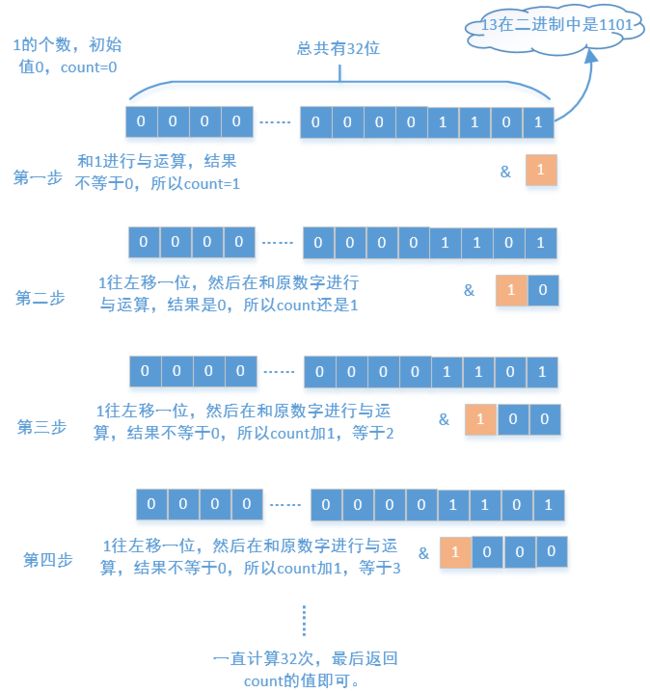
这次我们移动的是1,我们来看一下代码
public int bitCount(int n) {
int count = 0;
for (int i = 0; i < 32; i++) {
if ((n & (1 << i)) != 0) {
count++;
}
}
return count;
}
当然我们还可以通过运算的结果是否是1来判断也是可以的,我们只需要把往左移的1和n运算完之后再往右移即可,我们来看下代码
public int bitCount(int i) {
int count = 0;
for (int j = 0; j < 32; j++) {
if ((i & (1 << j)) >>> j == 1)
count++;
}
return count;
}
其他方法:
四:1每次往左移一位,把运算的结果在右移判断是否是1
public int hammingWeight(int i) {
int count = 0;
for (int j = 0; j < 32; j++) {
if ((i & (1 << j)) >>> j == 1)
count++;
}
return count;
}
五:这个是最常见的,每次消去最右边的1,直到消完为止
public int hammingWeight(int n) {
int count = 0;
while (n != 0) {
n &= n - 1;
count++;
}
return count;
}
六:把上面的改为递归
public int hammingWeight(int n) {
return n == 0 ? 0 : 1 + hammingWeight(n & (n - 1));
}
七:查表
public int hammingWeight(int i) {
//table是0到15转化为二进制时1的个数
int table[] = {0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4};
int count = 0;
while (i != 0) {//通过每4位计算一次,求出包含1的个数
count += table[i & 0xf];
i >>>= 4;
}
return count;
}
八:每两位存储,使用加法(先运算再移位)
public int hammingWeight(int n) {
n = ((n & 0xaaaaaaaa) >>> 1) + (n & 0x55555555);
n = ((n & 0xcccccccc) >>> 2) + (n & 0x33333333);
n = (((n & 0xf0f0f0f0) >>> 4) + (n & 0x0f0f0f0f));
n = n + (n >>> 8);
n = n + (n >>> 16);
return n & 63;
}
九:每两位存储,使用加法(先移位再运算)
public int hammingWeight(int n) {
n = ((n >>> 1) & 0x55555555) + (n & 0x55555555);
n = ((n >>> 2) & 0x33333333) + (n & 0x33333333);
n = (((n >>> 4) & 0x0f0f0f0f) + (n & 0x0f0f0f0f));
n = n + (n >>> 8);
n = n + (n >>> 16);
return n & 63;
}
十:和第8种思路差不多,只不过在最后几行计算的时候过滤的比较干净
public int hammingWeight(int n) {
n = ((n & 0xaaaaaaaa) >>> 1) + (n & 0x55555555);
n = ((n & 0xcccccccc) >>> 2) + (n & 0x33333333);
n = (((n & 0xf0f0f0f0) >>> 4) + (n & 0x0f0f0f0f));
n = (((n & 0xff00ff00) >>> 8) + (n & 0x00ff00ff));
n = (((n & 0xffff0000) >>> 16) + (n & 0x0000ffff));
return n;
}
十一:每4位存储,使用加法
public int hammingWeight(int n) {
n = (n & 0x11111111) + ((n >>> 1) & 0x11111111) + ((n >>> 2) & 0x11111111) + ((n >>> 3) & 0x11111111);
n = (((n & 0xf0f0f0f0) >>> 4) + (n & 0x0f0f0f0f));
n = n + (n >>> 8);
n = n + (n >>> 16);
return n & 63;
}
十二:每3位存储,使用加法
public int hammingWeight(int n) {
n = (n & 011111111111) + ((n >>> 1) & 011111111111) + ((n >>> 2) & 011111111111);
n = ((n + (n >>> 3)) & 030707070707);
n = ((n + (n >>> 6)) & 07700770077);
n = ((n + (n >>> 12)) & 037700007777);
return ((n + (n >>> 24))) & 63;
}
十三:每5位存储,使用加法
public int hammingWeight(int n) {
n = (n & 0x42108421) + ((n >>> 1) & 0x42108421) + ((n >>> 2) & 0x42108421) + ((n >>> 3) & 0x42108421) + ((n >>> 4) & 0x42108421);
n = ((n + (n >>> 5)) & 0xc1f07c1f);
n = ((n + (n >>> 10) + (n >>> 20) + (n >>> 30)) & 63);
return n;
}
十四:每两位存储,使用减法(先运算再移位)
public int hammingWeight(int i) {
i = i - ((i >>> 1) & 0x55555555);
i = (i & 0x33333333) + ((i >>> 2) & 0x33333333);
i = (i + (i >>> 4)) & 0x0f0f0f0f;
i = i + (i >>> 8);
i = i + (i >>> 16);
return i & 0x3f;
}
十五:每3位存储,使用减法
public int hammingWeight(int n) {
n = n - ((n >>> 1) & 033333333333) - ((n >>> 2) & 011111111111);
n = ((n + (n >>> 3)) & 030707070707);
n = ((n + (n >>> 6)) & 07700770077);
n = ((n + (n >>> 12)) & 037700007777);
return ((n + (n >>> 24))) & 63;
}
十六:每4位存储,使用减法
public int hammingWeight(int n) {
int tmp = n - ((n >>> 1) & 0x77777777) - ((n >>> 2) & 0x33333333) - ((n >>> 3) & 0x11111111);
tmp = ((tmp + (tmp >>> 4)) & 0x0f0f0f0f);
tmp = ((tmp + (tmp >>> 8)) & 0x00ff00ff);
return ((tmp + (tmp >>> 16)) & 0x0000ffff) % 63;
}
十七:每5位存储,使用减法
public int hammingWeight(int n) {
n = n - ((n >>> 1) & 0xdef7bdef) - ((n >>> 2) & 0xce739ce7) - ((n >>> 3) & 0xc6318c63) - ((n >>> 4) & 0x02108421);
n = ((n + (n >>> 5)) & 0xc1f07c1f);
n = ((n + (n >>> 10) + (n >>> 20) + (n >>> 30)) & 63);
return n;
}
十八:每次消去最右边的1,可以参照第5种解法
public static int hammingWeight(int num) {
int total = 0;
while (num != 0) {
num -= num & (-num);
total++;
}
return total;
}
这题如果一直写下去,再写10种也没问题,如果上面的代码你都能看懂,你也会有和我一样的想法。但解这题的最终思路还是没变,所以再写下去也没有太大价值。上面有些写法其实也很鸡肋,这里只是告诉大家这样写也是可以实现的,虽然可能你永远都不这样去写。
方法来源:
作者:数据结构和算法
链接:https://leetcode.cn/leetbook/read/top-interview-questions-easy/xn1m0i/?discussion=BDVi4v
来源:力扣(LeetCode)