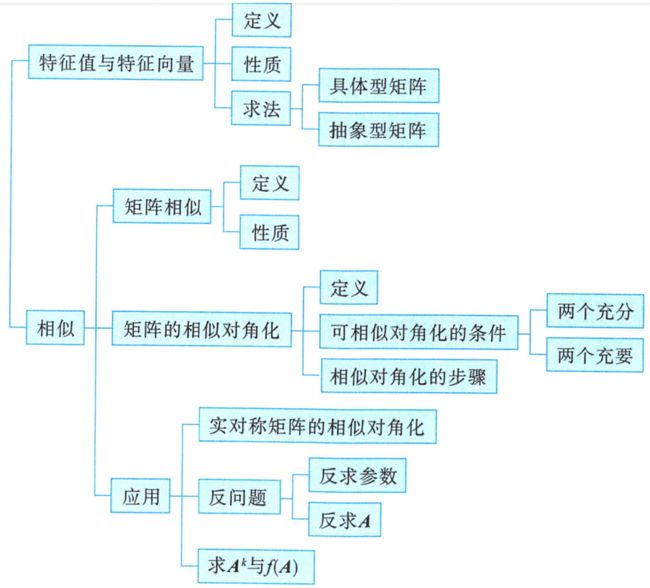
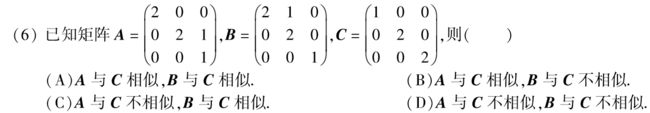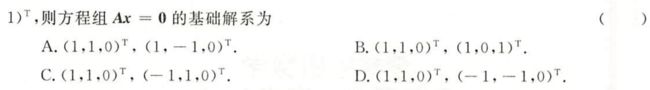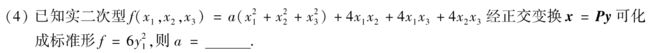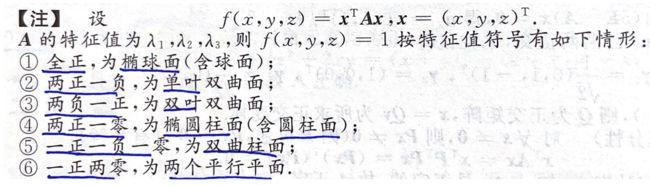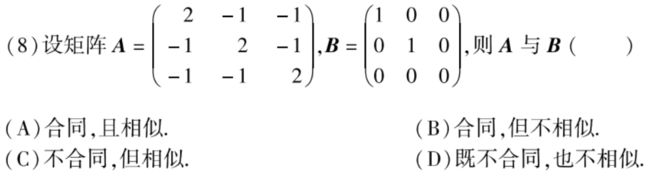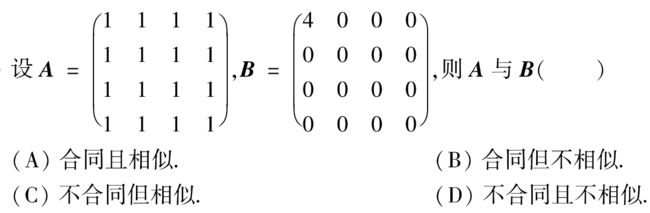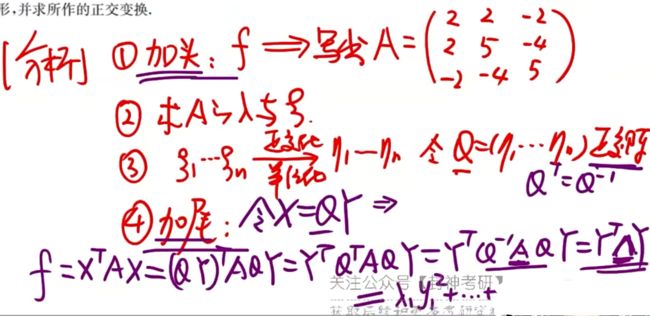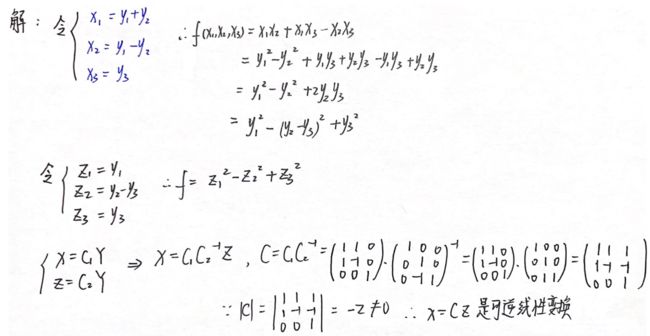线性代数(应用篇):第五章:特征值与特征向量、第六章:二次型
文章目录
-
- 第5章 特征值与特征向量、相似矩阵
- (一) 特征值与特征向量
-
- 1.定义
- 2.性质
- 3.求解
-
- (1)具体型矩阵
-
- 试根法、多项式带余除法:三阶多项式分解因式
- (2)抽象型矩阵
- (二) 相似
-
- 1.矩阵相似
-
- (1)定义
- (2)性质
- 2.相似对角化
-
- (1)定义
- (2)相似对角化的条件(n阶矩阵A可相似对角化的条件)
- (3)相似对角化的性质
- 3.实对称矩阵的相似对角化
-
- 1.实对称矩阵对角化的性质、步骤
- 2.正交矩阵、正交变换
-
- (1)正交矩阵Q
- (2)正交变换
- 3.反求参数、反求矩阵A、 A k A^k Ak
- 4.两矩阵是否相似的判别与证明
-
- (1)两个实对称/可相似对角化的矩阵相似的充要条件:
- (2)非实对称矩阵相似
- 第6章 二次型
- (一) 二次型的定义与矩阵表示
-
- 1.二次型定义
- 2.二次型的矩阵表示:二次型与矩阵的对应关系
- 3.二次型与二次曲面
- (二) 化二次型为标准型、规范型
-
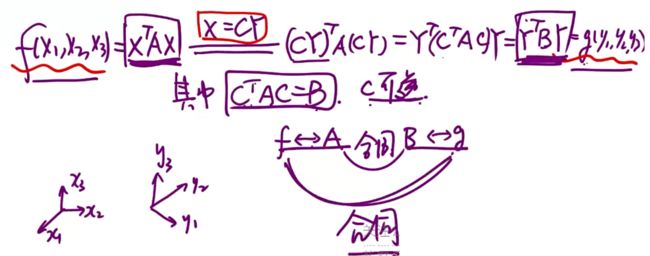
- 1.可逆线性变换 X=CY
- 2.合同
-
- (1)定义
- (2)性质
- (3)相似与合同
- 3.标准形、规范形
-
- (1)正交变换法 化二次型为标准形:得对角阵,系数为特征值
- (2)配方法 化二次型为标准形、规范形
- (三) 正定二次型
-
-
- 1.惯性定理
- 2.正定二次型、正定矩阵、 二次型正定性的判别
-
- (1)概念
- (2)性质(充要条件)
-
第5章 特征值与特征向量、相似矩阵
(一) 特征值与特征向量
1.定义
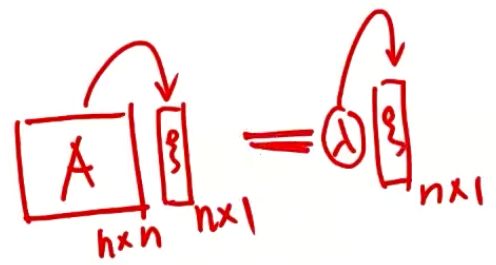
设 A A A是 n n n阶方阵, λ λ λ是一个数,若存在 n n n维非零列向量 ξ ξ ξ,使得 A ξ = λ ξ ( ξ ≠ 0 ) Aξ=λξ \quad (ξ≠0) Aξ=λξ(ξ=0)则称 λ λ λ是 A A A的特征值, ξ ξ ξ是 A A A的对应于(属于)特征值 λ λ λ的特征向量。
注:
①只有方阵才有特征值和特征向量
②n阶方阵有n个特征值

A n × n × ξ n × 1 = λ ξ n × 1 A_{n×n}×ξ_{n×1}=λξ_{n×1} An×n×ξn×1=λξn×1:即矩阵A作用在ξ上的效果,和一个数λ作用在ξ上的效果,是划等号的。即可用这个值来代表这个矩阵,即λ为矩阵的特征值。
其他概念:
①特征矩阵:λE-A
②特征多项式: f ( λ ) = ∣ λ E − A ∣ f(λ)=|λE-A| f(λ)=∣λE−A∣
③特征方程:f(λ)=|λE-A|=0
2.性质
1.特征值的性质:
(1)特征值之和 = 主对角线元素之和,特征值之积 = 行列式

(2)上下三角矩阵、对角阵的主对角线元素,就是特征值
(3)秩为1的实对称矩阵的特征值:λ₁=tr(A),λ₂=λ₃=0
2.特征向量的性质:
①k重特征值至多有k个线性无关的特征向量
②不同特征值对应的特征向量线性无关
③特征向量的线性组合,依然为特征向量 (只要求整体非零) (特征向量就是非零齐次解,齐次解的线性组合仍为齐次解)

3.求解
(1)具体型矩阵
①求特征值:解 ∣ λ E − A ∣ = 0 |λE-A|=0 ∣λE−A∣=0,求出n个 λ i λ_i λi
②求特征向量:将n个 λ i λ_i λi代回齐次线性方程组 ( λ i E − A ) x = 0 (λ_iE-A)x=0 (λiE−A)x=0,分别求出属于每个 λ i λ_i λi的非零解 ξ i ξ_i ξi,这是基础解系。则齐次方程组的通解去掉零解为 λ i λ_i λi的全部特征向量,即 k i ξ i k_iξ_i kiξi(ki≠0) 为对应于 λ i λ_i λi的全部特征向量。
试根法、多项式带余除法:三阶多项式分解因式
当该3阶矩阵的特征方程 ∣ λ E − A ∣ = 0 |λE-A|=0 ∣λE−A∣=0 不好求特征根时,可全部展开为3次多项式,使用试根法先求出一个根,得到 ( λ − λ 1 ) (λ-λ_1) (λ−λ1),再用多项式带余除法,得到 ( λ − λ 2 ) ( λ − λ 3 ) (λ-λ_2)(λ-λ_3) (λ−λ2)(λ−λ3)
1.试根法
对于 f ( λ ) = a k λ k + . . . + a 3 λ 3 + a 2 λ 2 + a 1 λ + a 0 = 0 f(λ)=a_kλ^k+...+a_3λ^3+a_2λ^2+a_1λ+a_0=0 f(λ)=akλk+...+a3λ3+a2λ2+a1λ+a0=0
①若 a 0 = 0 a_0=0 a0=0,则 f ( λ ) = 0 f(λ)=0 f(λ)=0 是根
②若 系数之和为0,则 f ( λ ) = 1 f(λ)=1 f(λ)=1 是根
③若 奇次方系数 = 偶次方系数,则 f ( λ ) = − 1 f(λ)=-1 f(λ)=−1 是根
④若 a k = 1 a_k=1 ak=1,各系数均为整数,则 根均为整数,且 根均为 a 0 a_0 a0的因子
例题2:真题,不太方便直接求出特征值,可考虑直接展开为3次多项式,用试根法+多项式带余除法

(2)抽象型矩阵
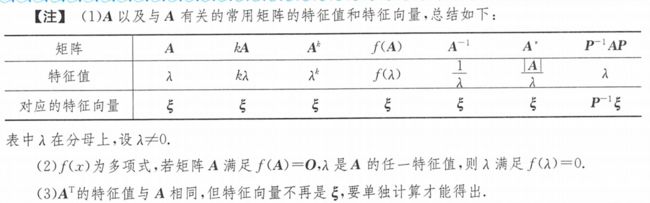
已经A的特征向量为ξ,则kA、A-1、A*、Ak、f(A)的特征向量均为ξ
但仅有 kA、A-1的特征向量为ξ时,也有A的特征向量为ξ
② ∣ λ E − A ∣ = 0 |λE-A|=0 ∣λE−A∣=0, ( λ E − A ) ξ = 0 (λE-A)ξ=0 (λE−A)ξ=0
③特征值的性质: ∣ A ∣ = λ 1 λ 2 . . . λ n , t r ( A ) = λ 1 + λ 2 + . . . + λ n = a 1 + a 2 + . . . + a n |A|=λ_1λ_2...λ_n,tr(A)=λ_1+λ_2+...+λ_n=a_1+a_2+...+a_n ∣A∣=λ1λ2...λn,tr(A)=λ1+λ2+...+λn=a1+a2+...+an
④特征向量的性质:特征向量的非零线性组合,仍为特征向量。【∴求特征向量时,求出基础解系是ξ后,要加k。最终的(全部的) 特征向量为kξ (k≠0)】
分析: λ ∗ = ∣ A ∣ λ λ^*=\dfrac{|A|}{λ} λ∗=λ∣A∣

答案:11
例题2:23李林六套卷(六)15. 特征值的性质:主对角线元素之和 = 迹 = 特征值之和

答案:1
例题3:18年13.

分析:特征向量的线性组合也为特征向量

答案:-1
(二) 相似
相似理论:①A~B ②A~Λ ③应用
1.矩阵相似
(1)定义
设A,B为n阶方阵,若存在可逆矩阵P,使得 P-1AP = B,则称 矩阵A与B相似,或称A,B是相似矩阵,记为A~B 。称P为A到B的相似变换矩阵或过渡矩阵。
(2)性质
若A、B相似,则 秩、行列式、迹、特征值相同。若可相似对角化,则相似于同一个对角阵。
(1)若 A ∼ B A\sim B A∼B,则
①行列式相等 ∣ A ∣ = ∣ B ∣ = λ 1 ⋅ λ 2 ⋅ λ 3 |A|=|B|=λ₁·λ₂·λ₃ ∣A∣=∣B∣=λ1⋅λ2⋅λ3 且 ∣ λ E − A ∣ = ∣ λ E − B ∣ |λE-A|=|λE-B| ∣λE−A∣=∣λE−B∣
②迹相等 t r ( A ) = t r ( B ) = λ 1 + λ 2 + λ 3 tr(A)=tr(B)=λ₁+λ₂+λ₃ tr(A)=tr(B)=λ1+λ2+λ3
③ A , B A,B A,B有相同的特征值 (特征值相同+实对称矩阵 → 相似)
④秩相等 r ( A ) = r ( B ) r(A)=r(B) r(A)=r(B) 、 r ( λ E − A ) = r ( λ E − B ) r(λE-A)=r(λE-B) r(λE−A)=r(λE−B)
⑤若A~B,则A等价于B,即A可通过初等变换化为B
这些性质只是必要条件,即使都满足,也无法证明 A~B
(2)若 A ∼ B ,则 { f ( A ) ∼ f ( B ) , A m ∼ B m A − 1 ∼ B − 1 ( 可逆 ) A ∗ ∼ B ∗ ( 可逆 ) A T ∼ B T A\sim B,则\left\{ \begin{aligned} f(A) &\sim f(B),A^m \sim B^m \\ A^{-1}& \sim B^{-1} \ (可逆) \\ A^* & \sim B^* \quad (可逆) \\ A^T & \sim B^T \end{aligned} \right. A∼B,则⎩ ⎨ ⎧f(A)A−1A∗AT∼f(B),Am∼Bm∼B−1 (可逆)∼B∗(可逆)∼BT
A~B,若A可逆,则 AB~BA。
证明:∵A可逆 ∴A-1(AB)A=BA ∴AB~BA
例题1:15年21.(1)、20年20.(1)
∵ A ∼ B ∴ { t r ( A ) = t r ( B ) ∣ A ∣ = ∣ B ∣ \quad∵A\sim B \qquad∴\left \{\begin{array}{cc} tr(A) = tr(B)\\ |A|=|B| \end{array}\right. ∵A∼B∴{tr(A)=tr(B)∣A∣=∣B∣
分析:需要掌握相似性质的证明
已知A~B,则若存在可逆矩阵P使得P-1AP = B。此题额外附加了A、B均为可逆矩阵的条件
①证明:A-1~B-1
∵P-1AP = B
对两边取逆
得 P-1A-1P = B-1,即A-1~B-1
②证明:AT~BT
∵P-1AP=B
对两边取转置
得 PTAT(P-1)T = BT
即 [(PT)-1]-1AT(PT)-1 = BT
令Q = (PT)-1 = (P-1)T,则 Q-1ATQ = BT,则 AT~BT
③在此题A、B均为可逆矩阵的前提下,D正确
P-1AP = B
P-1A-1P = B-1
∴P-1(A+A-1)P = B+B-1
④C,需要A、B均为实对称矩阵
答案:C
2.相似对角化
(1)定义
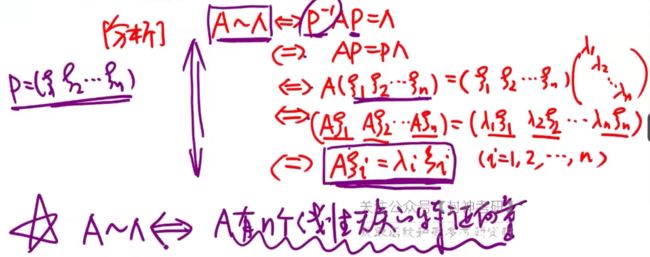
A可相似于对角阵,称为A可相似对角化,即:
对于n阶矩阵A,存在n阶可逆矩阵P,使得 P − 1 A P = Λ = ( λ 1 λ 2 λ 3 ) P^{-1}AP=Λ=\left(\begin{array}{cc} λ₁ & & \\ & λ₂ & \\ & & λ₃\\ \end{array}\right) P−1AP=Λ= λ1λ2λ3 ,其中 Λ Λ Λ为对角阵,记作 A ∼ Λ A\sim Λ A∼Λ,称A可相似对角化。称 Λ Λ Λ是A的相似标准形。
(2)相似对角化的条件(n阶矩阵A可相似对角化的条件)
| n阶矩阵A可相似对角化的条件 | |
| 充要条件 | ①A有n个线性无关的特征向量 |
| ②A的每一个k重特征值,都有k个线性无关的特征向量 即 k=n-r(λE-A),λ是k重根 |
|
| 充分条件 | ①A为实对称矩阵 |
| ②A有n个互异的特征值 | |
② k i = n − r ( λ i E − A ) k_i=n-r(λ_iE-A) ki=n−r(λiE−A), λ i λ_i λi是 k i k_i ki重根
注:
1.对于普通矩阵A:
①特征值不同 ( λ 1 ≠ λ 2 λ₁≠λ₂ λ1=λ2):特征向量 ξ 1 ξ 2 ξ₁ξ₂ ξ1ξ2一定线性无关
②特征值相同 ( λ 1 = λ 2 λ₁=λ₂ λ1=λ2):特征向量 ξ 1 ξ 2 ξ₁ξ₂ ξ1ξ2 可能无关,可能相关
2.A可相似对角化最本质的充要条件:A有n个线性无关的特征向量
(3)相似对角化的性质
相似的两矩阵若均可相似对角化,则可以相似于同一个对角矩阵。该对角矩阵的主对角线元素即为特征值 λ1、λ2、λ3
例题0:给定矩阵A,求可逆矩阵P,使得A可相似对角化,即 P − 1 A P = Λ P^{-1}AP=Λ P−1AP=Λ
步骤:①求特征值与特征向量 λ、ξ ②验证ξ₁,ξ₂,ξ₃线性无关 ③令 P = ( ξ 1 , ξ 2 , ξ 3 ) P=(ξ₁,ξ₂,ξ₃) P=(ξ1,ξ2,ξ3),验可逆 ④若P可逆,则有 P − 1 A P = Λ = ( λ 1 λ 2 λ 3 ) P^{-1}AP=Λ=\left(\begin{array}{cc} λ₁ & & \\ & λ₂ & \\ & & λ₃\\ \end{array}\right) P−1AP=Λ= λ1λ2λ3
分析:
A、B为上三角矩阵,C为对角矩阵。显然,A、B、C的特征值均为 2,2,1。
判断A、B是否与C相似, 即A、B能否相似对角化。
由相似对角化的充要条件:2重根,要有2个线性无关的特征向量,n-r(λE-A)=3-1=2 ∴r(λE-A)=1
显然,r(2E-A)=1,而r(2E-B)=2,∴A可以相似对角化,B不可以
答案:B
例题2:15年21.(2)
求可逆矩阵P,使P-1AP为对角矩阵:
只需求出其特征值,以及对应的n个线性无关的特征向量即可

分析:
①求特征值:A~B,∴A和B特征值相同。因为B的0更多,特征值更好求,所以用矩阵B来求特征值。
②求特征向量:分别将3个特征值λ代入λE-A,化简矩阵,得线性无关的特征向量
解题步骤:
①|λE-B|= |三阶行列式| =(λ-1)2(λ-5) ∴B的特征值为1,1,5
∵A~B ∴A的特征值也为1,1,5
②将λ=1代入(λE-A)x=0,即(E-A)x=0
E-A =()→(),得A的属于特征值λ=1的线性无关的特征向量为α1=( ),α2=( )
将λ=5代入(λE-A)x=0,即(5E-A)x=0
5E-A=()→(),得A的属于特征值λ=5的线性无关的特征向量为α3=( )
令P=(α1,α2,α3),则P-1AP = ʌ =()
例题4:20年20.(2)
3.实对称矩阵的相似对角化
1.实对称矩阵对角化的性质、步骤
1.实对称矩阵的性质
①实对称矩阵必能相似对角化
②实对称矩阵必有n个线性无关的特征向量
③实对称矩阵 不同特征值对应的特征向量一定正交
④实对称矩阵的特征值都是实数
⑤非零的幂零矩阵一定不能相似对角化
2.对于任一n阶实对称矩阵A,必存在正交矩阵Q,使得 Q − 1 A Q = Q T A Q = Λ = ( λ 1 λ 2 . . . λ n ) Q^{-1}AQ=Q^TAQ=Λ=\left(\begin{array}{cc} λ₁ & & \\ & λ₂ & \\ & & ...\\ &&& λ_n \end{array}\right) Q−1AQ=QTAQ=Λ= λ1λ2...λn
其中 λ 1 , λ 2 , . . . , λ n λ₁,λ₂,...,λ_n λ1,λ2,...,λn为A的n个实特征值,矩阵Q的列向量为A的依次对应于 λ 1 , λ 2 , . . . , λ n λ₁,λ₂,...,λ_n λ1,λ2,...,λn的两两正交的单位特征向量
3.根据上述结论,总结出正交变换矩阵Q将实对称矩阵A对角化的步骤为:
(1)求出A的全部特征值 λ 1 , λ 2 , . . . , λ n λ₁,λ₂,...,λ_n λ1,λ2,...,λn
(2)对每个特征值 λ i λ_i λi,求出其特征向量
(3)将特征向量正交化,再单位化
(4)将这些单位向量作为列向量构成正交矩阵Q,从而有 Q − 1 A Q = Q T A Q = Λ = ( λ 1 λ 2 . . . λ n ) Q^{-1}AQ=Q^TAQ=Λ=\left(\begin{array}{cc} λ₁ & & \\ & λ₂ & \\ & & ...\\ &&& λ_n \end{array}\right) Q−1AQ=QTAQ=Λ= λ1λ2...λn
答案:B
2.正交矩阵、正交变换
(1)正交矩阵Q
1.正交矩阵定义: Q Q T = Q T Q = E QQ^T=Q^TQ=E QQT=QTQ=E
两向量正交:内积为0
2.正交矩阵性质:(A,B均为n阶正交矩阵)
(1) Q − 1 = Q T Q^{-1}=Q^T Q−1=QT
(2) Q的各行向量两两正交,各列向量两两正交
(3) ∣ Q ∣ = ± 1 |Q|=±1 ∣Q∣=±1
(4) Q − 1 、 Q T 、 Q B Q^{-1}、Q^T、QB Q−1、QT、QB也是正交阵
(5)方阵Q是正交矩阵的充要条件:Q的列向量组或行向量组为标准正交向量组
3.求正交矩阵Q,使得 Q T A Q \rm Q^TAQ QTAQ为对角矩阵:
①求A的特征值:即求A的特征方程|λE-A|=0的全部解
②求A的特征向量:对求得的每一个特征值,将其代入 ( λ E − A ) x = 0 (λE-A)x=0 (λE−A)x=0,求出每个特征值对应的特征向量
③特征向量正交化
④特征向量单位化。然后组成正交矩阵Q

(2)正交变换
1.定义:
若Q为正交矩阵,则线性变换x=Qy称为正交变换。正交变换属于相似变换,不改变矩阵的特征值。
对任一n阶实对称矩阵A,必存在正交矩阵Q 使得A可以相似对角化,即 Q − 1 A Q = Q T A Q = Λ = ( λ 1 λ 2 . . . λ n ) Q^{-1}AQ=Q^TAQ=Λ=\left(\begin{array}{cc} λ₁ & & \\ & λ₂ & \\ & & ...\\ &&& λ_n \end{array}\right) Q−1AQ=QTAQ=Λ= λ1λ2...λn
2.性质:
(1)正交变换保持向量的内积不变
(2)正交变换保持向量的长度不变
(3)正交变换保持向量的夹角不变
只会将图形在坐标系中旋转,而不会扭曲图形
例题1:11年13. 正交变换不改变矩阵的特征值、行列式=特征值之积
![]()
答案:1
例题2:22年21.(2) ①二次型的定义 ②求正交矩阵、正交变换法化二次型为标准型 ③配方法

答案:
例题3:20年20(2)
3.反求参数、反求矩阵A、 A k A^k Ak
P − 1 A P = Λ P^{-1}AP=Λ P−1AP=Λ,则有:
① A = P Λ P − 1 A=PΛP^{-1} A=PΛP−1
② A k = P Λ k P − 1 A^k=PΛ^kP^{-1} Ak=PΛkP−1
③ f ( A ) = P f ( A ) P − 1 f(A)=Pf(A)P^{-1} f(A)=Pf(A)P−1
分析:
f ( λ 1 ) = f ( 1 ) = − 2 , f ( λ 2 ) = f ( 2 ) = − 2 , f ( λ 3 ) = f ( 3 ) = − 2 f(λ₁)=f(1)=-2,f(λ₂)=f(2)=-2,f(λ₃)=f(3)=-2 f(λ1)=f(1)=−2,f(λ2)=f(2)=−2,f(λ3)=f(3)=−2
B = f ( A ) = P f ( Λ ) P − 1 = P ( f ( λ 1 ) f ( λ 2 ) f ( λ 3 ) ) P − 1 = − 2 P E P − 1 = − 2 E B=f(A)=Pf(Λ)P^{-1}=P\left(\begin{array}{cc} f(λ₁) & & \\ & f(λ₂) & \\ & & f(λ₃)\\ \end{array}\right) P^{-1}=-2PEP^{-1}=-2E B=f(A)=Pf(Λ)P−1=P f(λ1)f(λ2)f(λ3) P−1=−2PEP−1=−2E
答案:-2E
4.两矩阵是否相似的判别与证明
1.判断A B 相似:
①定义法: P − 1 A P = B P^{-1}AP=B P−1AP=B,则 A ∼ B A \sim B A∼B
②传递法: A ∼ Λ 1 , B ∼ Λ 2 , λ A = λ B A\sim Λ₁,B\sim Λ₂,λ_A=λ_B A∼Λ1,B∼Λ2,λA=λB,则 Λ 1 = Λ 2 Λ₁=Λ₂ Λ1=Λ2,即 A ∼ Λ ∼ B A \sim Λ \sim B A∼Λ∼B
(1)两个实对称/可相似对角化的矩阵相似的充要条件:
两实对称矩阵/两可相似对角化的矩阵 相似 ⇦⇨ 特征多项式相同 ⇦⇨ 特征值全部相同
对于普通矩阵来说,特征多项式相同、特征值相同,只是相似的必要条件。
但对于两个 实对称/可对角化 的矩阵 来说,特征多项式相同、特征值相同等相似的必要条件,就变成了相似的充分必要条件。
证明:
1.若A、B均可相似对角化,且A、B特征值相同,则A、B相似于同一个对角阵。则 P − 1 A P = Λ , A ∼ Λ P − 1 B P = Λ , B ∼ Λ P^{-1}AP=Λ,A\sim Λ \qquad P^{-1}BP=Λ,B\sim Λ P−1AP=Λ,A∼ΛP−1BP=Λ,B∼Λ
由相似的传递性,可知 A ∼ Λ ∼ B , ∴ A ∼ B A\sim Λ \sim B,∴A\sim B A∼Λ∼B,∴A∼B
2.若A、B均为实对称矩阵。实对称矩阵一定可以相似对角化,再接1的证明
条件由强到弱依次是:
①实对称
②不对称但可相似对角化
③不对称,也不可相似对角化
(2)非实对称矩阵相似
(1)充要条件:若两矩阵相似,则特征矩阵也相似,则特征矩阵的秩相等。即 A ∼ B ⇦⇨ k E − A ∼ k E − B A\sim B \ \ ⇦⇨ \ \ kE-A\sim kE-B A∼B ⇦⇨ kE−A∼kE−B
(2)必要条件:A~B → r(A)=r(B)
λE-A ~ λE-B → r(λE-A) = r(λE-B)
分析:
显然,M、A、B、C、D的特征值均为1,1,1。 M ∼ A ⇦⇨ k E − M ∼ k E − A → r ( k E − M ) = r ( k E − A ) M\sim A\ \ ⇦⇨\ \ kE-M\sim kE-A \ → r(kE-M)=r(kE-A) M∼A ⇦⇨ kE−M∼kE−A →r(kE−M)=r(kE−A)
r(E-M)=2,r(E-A)=2,r(E-B)=r(E-C)=r(E-D)=1,∴E-M~E-A
答案:A
第6章 二次型
(一) 二次型的定义与矩阵表示
1.二次型定义
二次型的矩阵表达式: f ( x ) = x T A x f(x)=x^TAx f(x)=xTAx
即 f ( x 1 , x 2 , x 3 ) = ( x 1 , x 2 , x 3 ) ( a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ) ( x 1 x 2 x 3 ) = a 11 x 1 2 + a 22 x 2 2 + a 33 x 3 2 + f(x_1,x_2,x_3)=(x_1,x_2,x_3)\left(\begin{array}{cc} a₁₁ & a₁₂ & a₁₃ \\ a₂₁ & a₂₂ & a₂₃ \\ a₃₁ & a₃₂ & a₃₃ \\ \end{array}\right) \left(\begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array}\right)=a₁₁x₁^2+ a₂₂x₂^2+a₃₃x_3^2+ f(x1,x2,x3)=(x1,x2,x3) a11a21a31a12a22a32a13a23a33 x1x2x3 =a11x12+a22x22+a33x32+ ( a 12 + a 21 ) x 1 x 2 + ( a 13 + a 31 ) x 1 x 3 + ( a 23 + a 32 ) x 2 x 3 (a₁₂+a₂₁)x_1x_2+(a₁₃+a₃₁)x_1x_3+(a₂₃+a₃₂)x_2x_3 (a12+a21)x1x2+(a13+a31)x1x3+(a23+a32)x2x3
A为实对称矩阵 ( A = A T A=A^T A=AT),称为二次型的系数矩阵。
平方项: x i 2 x^2_i xi2、交叉项(混合项): x i x j 、 x j x i x_ix_j、x_jx_i xixj、xjxi
2.二次型的矩阵表示:二次型与矩阵的对应关系
1.看到二次型能写出矩阵,看到矩阵能写出它的二次型。
2.二次型f的矩阵,就是A,不能带x。二次型的定义是 f ( x ) = x T A x f(x)=x^TAx f(x)=xTAx
分析:对二次型进行正交变换得标准形,实际上就是对矩阵进行相似对角化。正交变换得到的标准形对应矩阵都是对角矩阵,标准形系数都是特征值。

答案:2
例题2:23李林六套卷(五)15. 二次型定义、合同的定义及性质

答案:

3.二次型与二次曲面
例题1:16年06. 二次型与二次曲面
![]()
答案:B
(二) 化二次型为标准型、规范型
1.可逆线性变换 X=CY
2.合同
(1)定义
设A,B为n阶方阵,若存在可逆矩阵C,使得 B = C T A C B=C^TAC B=CTAC,则称 矩阵A与B合同。记作 A ≃ B A\simeq B A≃B。此时称对应的二次型f(x)与g(y)为合同二次型。
(2)性质
1.两是对称矩阵A、B合同:
⇦⇨ A、B 正、负惯性指数 相同 【两合同矩阵的正负特征值个数相同】
⇦⇨ A、B 正惯性指数相同 + 秩相同
⇦⇨ p、q、r均相同
2.对称矩阵和不对称矩阵,不可能合同
证明:设A与B合同,A=AT,B≠BT。
存在可逆矩阵C,使得 CTAC=B①。两边取转置得,CTATC=BT
∵A=AT,得CTAC=BT②
∵B≠BT ∴①与②矛盾。故对称矩阵与不对称矩阵不合同。
(3)相似与合同
(两实对称矩阵)相似→合同:(实对称矩阵)相似 ⇨ 特征值相同 ⇨ 正负特征值个数一定相同 ⇨ 合同
两实对称矩阵:若相似,则一定合同。
对称矩阵与非对称矩阵,一定不合同。
例题1:
分析:相似还是合同,只需要看特征值

由|λE-A|=0求得A的特征值为3,3,0。对角阵B的特征值为1,1,0。可见AB特征值不相同,不相似。但是 正惯性指数和秩相同,因此AB合同。
答案:B
分析:A、B均为实对称矩阵
由|λE-A|=0求得A的特征值为 λ₁=4,λ₂=λ₃=λ₄=0
对角阵B的特征值也为λ₁=4,λ₂=λ₃=λ₄=0
特征值相同,∴A、B相似。
特征值相同,则正负惯性指数也必然相同,∴A、B合同
答案:A
3.标准形、规范形
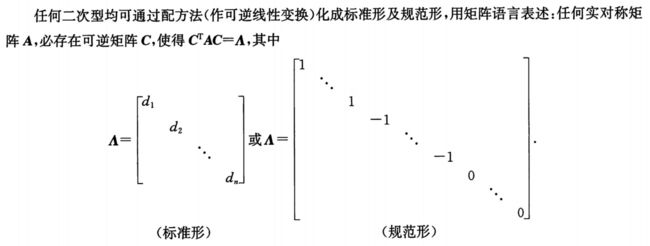
1.标准形:
与对角矩阵对应的二次型f( 只含有平方项),即为标准形。
2.规范形:
平方项的系数为+1或-1
①为什么要化为“标准形”、“规范形”?
答:标准形、规范形只含平方项,二次型对应的二次曲面方便找出最大值。
②如何化为标准形、规范形?
对A做相似对角化,化为相似的对角阵,主对角线元素均为特征值。满足只含平方项。
分析:
(1)平方和为0,则每个括号内都为0
(2)
(1)正交变换法 化二次型为标准形:得对角阵,系数为特征值
1.定理
任意给定实二次型 f = x T A x ( A T = A ) f=x^TAx\quad(A^T=A) f=xTAx(AT=A),一定存在正交变换 x = Q y x=Qy x=Qy,使f 化为标准形 f = λ 1 y 1 2 + λ 2 y 2 2 + . . . + λ n y n 2 f= λ_1y_1^2+λ_2y_2^2+...+λ_ny_n^2 f=λ1y12+λ2y22+...+λnyn2 。其中 λ i ( i = 1 , 2 , . . . , n ) λ_i(i=1,2,...,n) λi(i=1,2,...,n)为二次型矩阵A的特征值。
2.性质
①正交变换相当于对实对称矩阵A做了相似对角化,得到的平方项系数即为A的特征值。【而配方法得到的系数一般不是特征值。】
②正交变换法只能化二次型为标准形,不能化为规范形(除非特征值都属于{1,-1,0})
3.用正交变换化二次型为标准形的步骤:
(1)写出二次型对应的实对称矩阵A
(2)求出A的所有特征值和特征向量
(3)将特征向量正交化、单位化,得η1,η2,…,ηn,得正交矩阵Q=(η1,η2,…,ηn)
(4)作正交变换 x=Qy,得f的标准形: f = x T A x = x = Q y ( Q y ) T A Q y = y T ( Q T A Q ) y = y T ( Q − 1 A Q ) y = y T Λ y = λ 1 y 1 2 + λ 2 y 2 2 + . . . + λ n y n 2 f=x^TAx\xlongequal{\rm x=Qy}(Qy)^TAQy=y^T(Q^TAQ)y=y^T(Q^{-1}AQ)y=y^TΛy=λ_1y_1^2+λ_2y_2^2+...+λ_ny_n^2 f=xTAxx=Qy(Qy)TAQy=yT(QTAQ)y=yT(Q−1AQ)y=yTΛy=λ1y12+λ2y22+...+λnyn2
其中正交变换为 x = Q y = ( 正交矩阵 Q ) ( 列向量 y ) x=Qy=(正交矩阵Q)(列向量y) x=Qy=(正交矩阵Q)(列向量y)
答案:A
分析:
(1)①二次型与矩阵的对应关系 ②正交变换也是相似变换
(2) ∵二阶矩阵A、B均有2个互异的特征值,∴A、B均可相似对角化
且∵A~B,∴A、B相似于同一个对角矩阵
设A ~ Λ,则存在可逆矩阵P1使得 P 1 − 1 A P 1 = Λ P_1^{-1}AP_1=Λ P1−1AP1=Λ
设B ~ Λ,则存在可逆矩阵P2使得 P 2 − 1 B P 2 = Λ P_2^{-1}BP_2=Λ P2−1BP2=Λ
∴ B = P 2 Λ P 2 − 1 = P 2 P 1 − 1 A P 1 P 2 − 1 ∴B=P_2ΛP_2^{-1}=P_2P_1^{-1}AP_1P_2^{-1} ∴B=P2ΛP2−1=P2P1−1AP1P2−1
令 P = P 1 P 2 − 1 P=P_1P_2^{-1} P=P1P2−1, ∴ B = P − 1 A P ∴B=P^{-1}AP ∴B=P−1AP
所以,求出P1、P2,得 P = P 1 P 2 − 1 P=P_1P_2^{-1} P=P1P2−1。对P进行正交化单位化,得正交矩阵Q
分析:秩的性质、正交变换的步骤
答案:(1)a = -1
(2)配方法 化二次型为标准形、规范形
配方法:
①将某个 x i x_i xi的平方项及与其有关的混合项,一次性配成一个完全平方。如此,直到全部配成完全平方项。
②n元要n换,缺项要补项(+0倍 x 3 x_3 x3,令 y 3 = x 3 y_3=x_3 y3=x3),得到 Y = C − 1 X Y=C^{-1}X Y=C−1X
③反解出C,即 X=CY
若要化二次型为规范形,只可使用配方法。正交变换法只能化到标准形,正交变换化的标准形的系数是实对称矩阵A的特征值。

例题1:没有平方项,创造平方项
![]()
分析:化为规范形,只能使用配方法
例题2:14年13. 配方法求二次型的标准形
![]()
答案:[-2,2]
(三) 正定二次型
1.惯性定理
①正惯性指数p:正特征值的个数
②负惯性指数q:负特征值的个数。满秩时,负惯性指数为奇数,行列式<0
③ r = p + q r=p+q r=p+q
分析:
求特征值时,不可进行初等变换(初等变换会改变特征值),不要化为行最简。此题直接求特征值困难。
满秩时,负惯性指数为奇数,行列式<0
答案:[-2,2]
2.正定二次型、正定矩阵、 二次型正定性的判别
(1)概念
设 f = x T A x ( A T = A ) f=x^TAx \ (A^T=A) f=xTAx (AT=A)为实二次型,若对于任意非零向量 x x x,
(1)恒有 xTAx >0,则称 f=xTAx 为正定二次型,称矩阵A为正定矩阵;
恒有 xTAx <0,则称f=xTAx 为负定二次型,称矩阵A为负定矩阵;
(2)恒有 xTAx ≥ 0,则称 f=xTAx为 半正定二次型,称矩阵A为半正定矩阵;
恒有 xTAx ≤ 0,则称 f=xTAx为 半负定二次型,称矩阵A为半负定矩阵;
(3)若f=xTAx的值时而为正,时而为负,则称 f=xTAx 为不定二次型
(2)性质(充要条件)
矩阵A正定 (抽象型矩阵:先说A是实对称, A T = A A^T=A AT=A,再用充要条件)
⇦⇨ ①A的各阶顺序主子式 Δ i > 0 Δ_i>0 Δi>0 (从左上角或右下角开始都可) 【具体型矩阵】
⇦⇨ ②A的所有特征值均为正值 λ i > 0 λ_i>0 λi>0 【具体型、抽象型】
⇦⇨ ③A的正惯性指数 p = r = n p=r=n p=r=n 【配方法求】
⇦⇨ ④对任意n维非零列向量 x x x,总有 f = x T A x > 0 f=x^TAx>0 f=xTAx>0 (正定的定义)
⇦⇨ ⑤A与单位阵E合同,即 P T A P = E P^TAP=E PTAP=E
⇦⇨ ⑥存在可逆矩阵Q,使得 A = Q T Q A=Q^TQ A=QTQ