剑指offor刷题---java版
面试题03. 数组中重复的数字
找出数组中重复的数字。
在一个长度为 n 的数组 nums 里的所有数字都在 0~n-1 的范围内。数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。
示例 1:
输入:
[2, 3, 1, 0, 2, 5, 3]
输出:2 或 3
class Solution {
public int findRepeatNumber(int[] nums) {
/**方法一 暴力双循环
for (int i = 0;i
Set<Integer> set = new HashSet<>();
int index = -1;
for(int num : nums){
if(!set.add(num)){
index = num;
}
}
return index;
}
}
面试题04. 二维数组中的查找
在一个 n * m 的二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
示例:现有矩阵 matrix 如下:
[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]
给定 target = 5,返回 true。
给定 target = 20,返回 false。
class Solution {
public static boolean findNumberIn2DArray(int[][] matrix, int target) {
if(matrix == null || matrix.length == 0 || matrix[0].length == 0){
return false;
}
//行数
int rows = matrix.length;
//列数
int cols = matrix[0].length;
int r =0,c =cols -1;//从右上角开始遍历数组元素
while(r<rows & c>=0){
if(matrix[r][c] == target){
return true;
}else if(matrix[r][c] > target){
c--;
}else{
r++;
}
}
return false;
}
}
面试题05. 替换空格
请实现一个函数,把字符串 s 中的每个空格替换成"%20"。
示例 1:
输入:s = “We are happy.”
输出:“We%20are%20happy.”
class Solution {
public static String replaceSpace(String s) {
StringBuffer str = new StringBuffer(s);
int p1 = str.length()-1;
for(int i = 0;i <= p1; i++){
if(str.charAt(i) == ' '){
str.append(" ");
}
}
int p2 = str.length()-1;
while(p1 >= 0 && p2>p1 ){
char c = s.charAt(p1--);
if(c == ' '){
str.setCharAt(p2--,'0');
str.setCharAt(p2--,'2');
str.setCharAt(p2--,'%');
}else{
str.setCharAt(p2--,c);
}
}
return str.toString();
}
}
面试题06. 从尾到头打印链表
输入一个链表的头节点,从尾到头反过来返回每个节点的值(用数组返回)。示例 1:
输入:head = [1,3,2]
输出:[2,3,1]
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public int[] reversePrint(ListNode head) {
ArrayList<Integer> al = new ArrayList<>();
while(head != null){
al.add(head.val);
head = head.next;
}
int[] arr = new int[al.size()];
for(int i = 0;i<al.size();i++){
arr[i] = al.get(i);
}
for(int i=0,j=arr.length-1;i<=j;i++,j--){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
return arr;
}
}
面试题07. 重建二叉树
输入某二叉树的前序遍历和中序遍历的结果,请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
例如,给出前序遍历 preorder = [3,9,20,15,7]中序遍历 inorder = [9,3,15,20,7]返回如下的二叉树:
3
/
9 20
/
15 7
限制:
0 <= 节点个数 <= 5000
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
int preindex = 0,inindex = 0;
public TreeNode buildTree(int[] preorder, int[] inorder) {
return dfs(preorder,inorder,null);
}
private TreeNode dfs(int[] preorder,int[] inorder,TreeNode finish){
if(preindex == preorder.length || (finish != null && finish.val == inorder[inindex]))
return null;
TreeNode root = new TreeNode(preorder[preindex++]);//根结点
//左节点
root.left = dfs(preorder,inorder,root);
inindex++;
//右节点
root.right = dfs(preorder,inorder,finish);
//返回null的情况
return root;
}
}
面试题09. 用两个栈实现队列
用两个栈实现一个队列。队列的声明如下,请实现它的两个函数 appendTail 和 deleteHead ,分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素,deleteHead 操作返回 -1 )
示例 1:输入:
[“CQueue”,“appendTail”,“deleteHead”,“deleteHead”]
[[],[3],[],[]]
输出:[null,null,3,-1]
示例 2:输入:
[“CQueue”,“deleteHead”,“appendTail”,“appendTail”,“deleteHead”,“deleteHead”]
[[],[],[5],[2],[],[]]
输出:[null,-1,null,null,5,2]
提示:1 <= values <= 10000
最多会对 appendTail、deleteHead 进行 10000 次调用
class CQueue {
Stack stk1,stk2;
int size;
public CQueue() {
stk1 = new Stack<Integer>();
stk2 = new Stack<Integer>();
size = 0;
}
public void appendTail(int value) {
while(!stk1.isEmpty())
stk2.push(stk1.pop());
stk1.push(value);
size++;
while(!stk2.isEmpty())
stk1.push(stk2.pop());
}
public int deleteHead() {
if(size == 0){
return -1;
}
int res = (int) stk1.pop();
size--;
return res;
}
}
面试题10- I. 斐波那契数列
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项。斐波那契数列的定义如下:
F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始,之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入:n = 2
输出:1
示例 2:
输入:n = 5
输出:5
提示:0 <= n <= 100
class Solution {
public int fib(int n) {
if(n == 0)
return 0;
if(n == 1)
return 1;
int first = 0;
int second = 1;
int res = 0;
for (int i = 2; i <= n ;i++){
res = (first+second) % 1000000007;
first = second % 1000000007;
second = res % 1000000007;
}
return res % 1000000007;
}
}
面试题10- II. 青蛙跳台阶问题
只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1
输入:n = 2
输出:2
示例 2:
输入:n = 7
输出:21
提示:0 <= n <= 100
class Solution {
public int numWays(int n) {
if(n == 0)
return 1;
if(n == 1)
return 1;
int first = 1;
int second = 1;
int res = 0;
for (int i = 2; i <= n ;i++){
res = (first+second) % 1000000007;
first = second % 1000000007;
second = res % 1000000007;
}
return res % 1000000007;
}
}
面试题11. 旋转数组的最小数字
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个递增排序的数组的一个旋转,输出旋转数组的最小元素。例如,数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一个旋转,该数组的最小值为1。
示例 1:
输入:[3,4,5,1,2]
输出:1
示例 2:
输入:[2,2,2,0,1]
输出:0
class Solution {
public int minArray(int[] numbers) {
if(numbers.length == 0) return 0;
int min = numbers[0];
for (int i : numbers) {
if(i<min)
return i;
}
return min;
}
}
面试题12. 矩阵中的路径
请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一格开始,每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格,那么该路径不能再次进入该格子。例如,在下面的3×4的矩阵中包含一条字符串“bfce”的路径(路径中的字母用加粗标出)。
[[“a”,“b”,“c”,“e”],
[“s”,“f”,“c”,“s”],
[“a”,“d”,“e”,“e”]]
但矩阵中不包含字符串“abfb”的路径,因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后,路径不能再次进入这个格子。
示例 1:
输入:board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCCED”
输出:true
示例 2:
输入:board = [[“a”,“b”],[“c”,“d”]], word = “abcd”
输出:false
提示:
1 <= board.length <= 200
1 <= board[i].length <= 200
class Solution {
public boolean exist(char[][] board, String word) {
for(int i = 0;i < board.length;i++){
for(int j = 0;j<board[0].length;j++){
if(dfs(board,word,0,i,j))
return true;
}
}
return false;
}
public boolean dfs(char[][] board,String word,int i,int x,int y){
if(x >= board.length || x < 0 || y >= board[0].length || y < 0 || board[x][y] != word.charAt(i) )
return false;
if(i == word.length() - 1)
return true;
char temp = board[x][y];
board[x][y] = '*';
boolean flag = dfs(board,word,i + 1,x + 1,y) || dfs(board,word,i + 1,x - 1,y) || dfs(board,word,i + 1,x ,y + 1)
|| dfs(board,word,i + 1,x,y - 1);
board[x][y] = temp;
return flag;
}
}
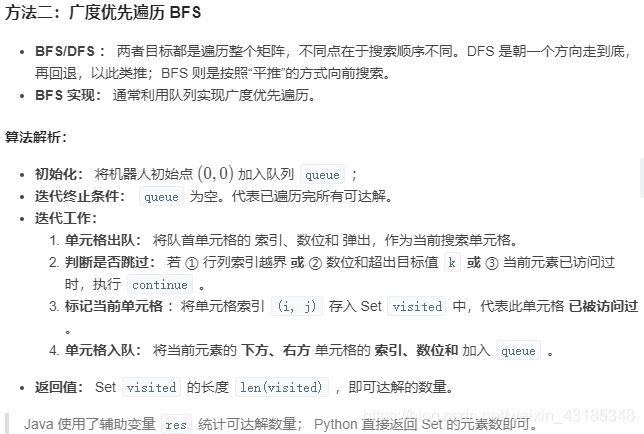
面试题13. 机器人的运动范围
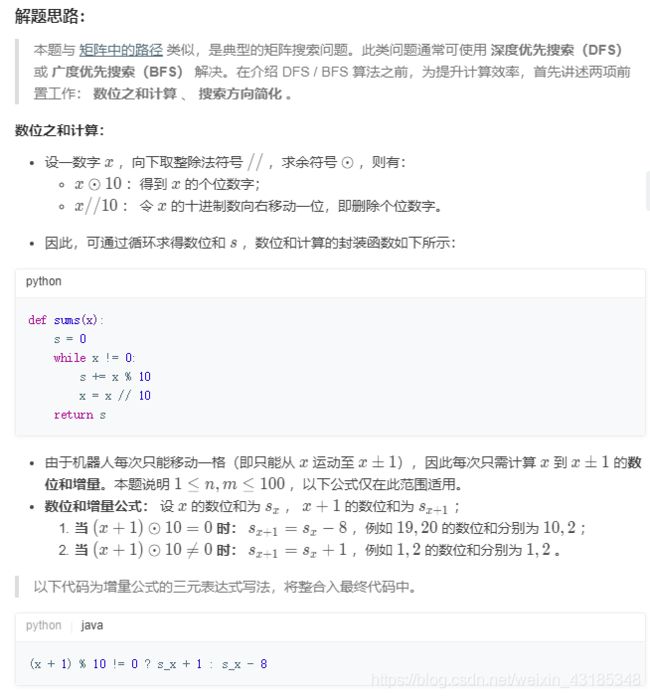
地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],因为3+5+3+8=19。请问该机器人能够到达多少个格子?
示例 1:
输入:m = 2, n = 3, k = 1
输出:3
示例 2:
输入:m = 3, n = 1, k = 0
输出:1
提示:
1 <= n,m <= 100
0 <= k <= 20

class Solution {
int m, n, k;
boolean[][] visited;
public int movingCount(int m, int n, int k) {
this.m = m; this.n = n; this.k = k;
this.visited = new boolean[m][n];
return dfs(0, 0, 0, 0);
}
public int dfs(int i, int j, int si, int sj) {
if(i >= m || j >= n || k < si + sj || visited[i][j]) return 0;
visited[i][j] = true;
return 1 + dfs(i + 1, j, (i + 1) % 10 != 0 ? si + 1 : si - 8, sj) + dfs(i, j + 1, si, (j + 1) % 10 != 0 ? sj + 1: sj - 8);
}
}
class Solution {
public int movingCount(int m, int n, int k) {
boolean[][] visited = new boolean[m][n];
int res = 0;
Queue<int[]> queue= new LinkedList<int[]>();
queue.add(new int[] { 0, 0, 0, 0 });
while(queue.size() > 0) {
int[] x = queue.poll();
int i = x[0], j = x[1], si = x[2], sj = x[3];
if(i >= m || j >= n || k < si + sj || visited[i][j]) continue;
visited[i][j] = true;
res ++;
queue.add(new int[] { i + 1, j, (i + 1) % 10 != 0 ? si + 1 : si - 8, sj });
queue.add(new int[] { i, j + 1, si, (j + 1) % 10 != 0 ? sj + 1 : sj - 8 });
}
return res;
}
}
面试题14- I. 剪绳子
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]…k[m-1] 。请问 k[0]k[1]…*k[m-1] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
示例 1:
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1
示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36
提示:
class Solution {
public int cuttingRope(int n) {
if(n <= 3) return n - 1;
int a = n / 3, b = n % 3;
if(b == 0) return (int)Math.pow(3, a);
if(b == 1) return (int)Math.pow(3, a - 1) * 4;
return (int)Math.pow(3, a) * 2;
}
}
面试题14- II. 剪绳子 II
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]…k[m] 。请问 k[0]k[1]…*k[m] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1
示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36
提示:
2 <= n <= 1000
class Solution {
public int cuttingRope(int n) {
long res = 1;
if(n <= 3)
return n - 1;
while(n > 4){
res = (res * 3) % 1000000007;
n -= 3;
}
return (int)(res * n % 1000000007);
}
}
面试题15. 二进制中1的个数
请实现一个函数,输入一个整数,输出该数二进制表示中 1 的个数。例如,把 9 表示成二进制是 1001,有 2 位是 1。因此,如果输入 9,则该函数输出 2。
示例 1:
输入:00000000000000000000000000001011
输出:3
解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 ‘1’。
示例 2:
输入:00000000000000000000000010000000
输出:1
解释:输入的二进制串 00000000000000000000000010000000 中,共有一位为 ‘1’。
示例 3:
输入:11111111111111111111111111111101
输出:31
解释:输入的二进制串 11111111111111111111111111111101 中,共有 31 位为 ‘1’。

public class Solution {
public int hammingWeight(int n) {
int res = 0;
while(n != 0) {
res += n & 1;
n >>>= 1;
}
return res;
}
}
public class Solution {
public int hammingWeight(int n) {
int res = 0;
while(n != 0) {
res++;
n &= n - 1;
}
return res;
}
}
面试题16. 数值的整数次方
实现函数double Power(double base, int exponent),求base的exponent次方。不得使用库函数,同时不需要考虑大数问题。
示例 1:
输入: 2.00000, 10
输出: 1024.00000
示例 2:
输入: 2.10000, 3
输出: 9.26100
示例 3:
输入: 2.00000, -2
输出: 0.25000
解释: 2-2 = 1/22 = 1/4 = 0.25
说明:
-100.0 < x < 100.0
n 是 32 位有符号整数,其数值范围是 [−231, 231 − 1] 。



class Solution {
public double myPow(double x, int n) {
if(x == 0) return 0;
long b = n;
double res = 1.0;
if(b < 0) {
x = 1 / x;
b = -b;
}
while(b > 0) {
if((b & 1) == 1) res *= x;
x *= x;
b >>= 1;
}
return res;
}
}
要注意的一点是,虽然题目中告诉我们不需要考虑大数问题,但是给出的 n 可以取到 -2147483648−2147483648(整型负数的最小值),因此,在编码的时候,需要将 n 转换成 long 类型
写法一:递归写法(分治思想)
public class Solution {
public double myPow(double x, int n) {
// 特判,也可以认为是递归终止条件
long N = n;
if (N < 0) {
return 1 / myPow(x, -N);
}
return myPow(x, N);
}
private double myPow(double x, long n) {
if (n == 0) {
return 1;
}
if (x == 1) {
return 1;
}
// 根据指数是奇数还是偶数进行分类讨论
// 使用位运算的 与 运算符代替了求余数运算
if ((n % 2) == 0) {
// 分治思想:分
double square = myPow(x, n / 2);
// 分治思想:合,下面同理
return square * square;
} else {
// 是奇数的时候
double square = myPow(x, (n - 1) / 2);
return square * square * x;
}
}
}
写法二:非递归写法(将指数看成二进制数)
把指数 n 做“二进制分解”,在底数不断自身乘以自身的过程中,将最终结果需要的部分保存下来

public class Solution {
public double myPow(double x, int n) {
long N = n;
if (N < 0) {
x = 1 / x;
N *= -1;
}
double res = 1;
while (N > 0) {
if ((N % 2) == 1) {
res *= x;
}
x *= x;
N /= 2;
}
return res;
}
}
面试题17. 打印从1到最大的n位数
输入数字 n,按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3,则打印出 1、2、3 一直到最大的 3 位数 999。
示例 1:
输入: n = 1
输出: [1,2,3,4,5,6,7,8,9]
class Solution {
public int[] printNumbers(int n) {
int finalNum = 0;
while(n != 0){
finalNum += (int) (9 * Math.pow(10, n-1));
n--;
}
System.out.println(finalNum);
int[] res = new int[finalNum];
for (int i = 0;i<finalNum;i++){
res[i] = i + 1;
}
return res;
}
}
面试题18. 删除链表的节点
给定单向链表的头指针和一个要删除的节点的值,定义一个函数删除该节点。
返回删除后的链表的头节点。
注意:此题对比原题有改动
示例 1:
输入: head = [4,5,1,9], val = 5
输出: [4,1,9]
解释: 给定你链表中值为 5 的第二个节点,那么在调用了你的函数之后,该链表应变为 4 -> 1 -> 9.
示例 2:
输入: head = [4,5,1,9], val = 1
输出: [4,5,9]
解释: 给定你链表中值为 1 的第三个节点,那么在调用了你的函数之后,该链表应变为 4 -> 5 -> 9
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode deleteNode(ListNode head, int val) {
if(head == null)return null;
if(head.val == val) return head.next;
ListNode res = head;
while(res.next.val != val){
res = res.next;
}
res.next = res.next.next;
return head;
}
}
面试题19. 正则表达式匹配
请实现一个函数用来匹配包含’. ‘和’‘的正则表达式。模式中的字符’.‘表示任意一个字符,而’'表示它前面的字符可以出现任意次(含0次)。在本题中,匹配是指字符串的所有字符匹配整个模式。例如,字符串"aaa"与模式"a.a"和"abaca"匹配,但与"aa.a"和"ab*a"均不匹配。
示例 1:
输入:
s = “aa”
p = “a”
输出: false
解释: “a” 无法匹配 “aa” 整个字符串。
示例 2:
输入:
s = “aa”
p = “a*”
输出: true
解释: 因为 ‘*’ 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 ‘a’。因此,字符串 “aa” 可被视为 ‘a’ 重复了一次。
示例 3:
输入:
s = “ab”
p = “."
输出: true
解释: ".” 表示可匹配零个或多个(’*’)任意字符(’.’)。
示例 4:
输入:
s = “aab”
p = “cab”
输出: true
解释: 因为 ‘*’ 表示零个或多个,这里 ‘c’ 为 0 个, ‘a’ 被重复一次。因此可以匹配字符串 “aab”。
示例 5:
输入:
s = “mississippi”
p = “misisp*.”
输出: false
s 可能为空,且只包含从 a-z 的小写字母。
p 可能为空,且只包含从 a-z 的小写字母以及字符 . 和 ,无连续的 '’。


class Solution {
public boolean isMatch(String A, String B) {
int n = A.length();
int m = B.length();
boolean[][] f = new boolean[n + 1][m + 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= m; j++) {
//分成空正则和非空正则两种
if (j == 0) {
f[i][j] = i == 0;
} else {
//非空正则分为两种情况 * 和 非*
if (B.charAt(j - 1) != '*') {
if (i > 0 && (A.charAt(i - 1) == B.charAt(j - 1) || B.charAt(j - 1) == '.')) {
f[i][j] = f[i - 1][j - 1];
}
} else {
//碰到 * 了,分为看和不看两种情况
//不看
if (j >= 2) {
f[i][j] |= f[i][j - 2];
}
//看
if (i >= 1 && j >= 2 && (A.charAt(i - 1) == B.charAt(j - 2) || B.charAt(j - 2) == '.')) {
f[i][j] |= f[i - 1][j];
}
}
}
}
}
return f[n][m];
}
}
面试题20. 表示数值的字符串
请实现一个函数用来判断字符串是否表示数值(包括整数和小数)。例如,字符串"+100"、“5e2”、"-123"、“3.1416”、“0123"都表示数。但"12e”、“1a3.14”、“1.2.3”、“±5”、"-1E-16"及"12e+5.4"都不是。
class Solution {
public boolean isNumber(String s) {
char[] ch = s.trim().toCharArray();
boolean num = false;
boolean dot = false;
boolean e = false;
for(int i = 0; i < ch.length; i++){
char c = ch[i];
if(c >= '0' && c <= '9'){
num = true;
} else if(c == 'e'){
if(!num || e)
return false;
e = true;
num = false;
} else if(c == '.'){
if(dot || e)
return false;
dot = true;
} else if(c == '+' || c == '-'){
if(i != 0 && ch[i-1] != 'e' && ch[i-1] != 'E'){
return false;
}
}else{
return false;
}
}
return num;
}
}
面试题21. 调整数组顺序使奇数位于偶数前面
输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有奇数位于数组的前半部分,所有偶数位于数组的后半部分。
示例:
输入:nums = [1,2,3,4]
输出:[1,3,2,4]
注:[3,1,2,4] 也是正确的答案之一。
提示:
1 <= nums.length <= 50000
1 <= nums[i] <= 10000
class Solution {
public int[] exchange(int[] nums) {
int i = 0, j = nums.length - 1, tmp;
while(i < j) {
while((i < j) && (nums[i] & 1) == 1) i++;
while((i < j) && (nums[j] & 1) == 0) j--;
tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
return nums;
}
}
面试题22. 链表中倒数第k个节点
输入一个链表,输出该链表中倒数第k个节点。为了符合大多数人的习惯,本题从1开始计数,即链表的尾节点是倒数第1个节点。例如,一个链表有6个节点,从头节点开始,它们的值依次是1、2、3、4、5、6。这个链表的倒数第3个节点是值为4的节点。
示例:
给定一个链表: 1->2->3->4->5, 和 k = 2.
返回链表 4->5.
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode getKthFromEnd(ListNode head, int k) {
ListNode pre = head,lat = head;
for(int i = 0;i < k; i++){
pre = pre.next;
}while(pre != null){
pre = pre.next;
lat = lat.next;
}
return lat;
}
}
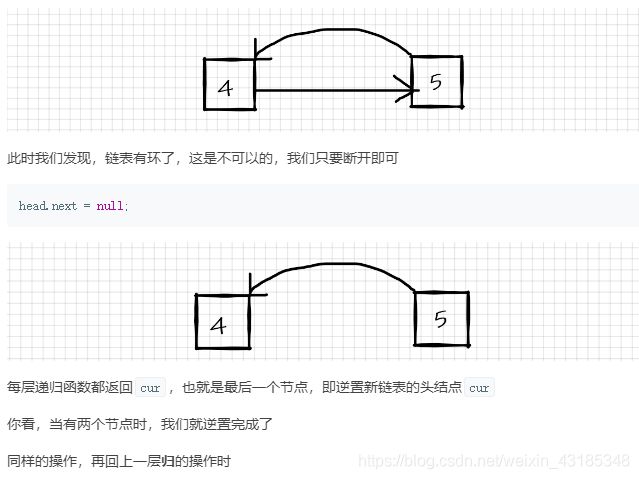
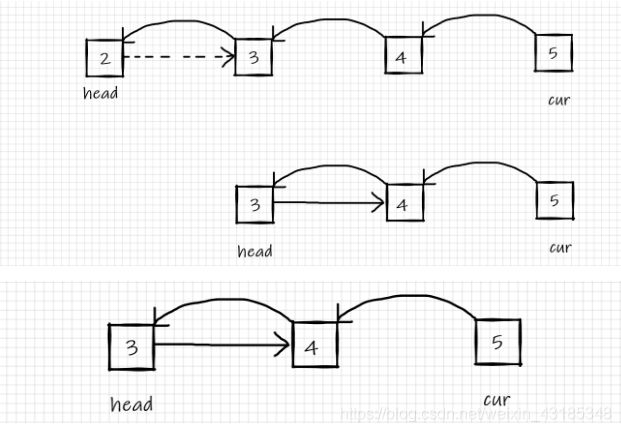
面试题24. 反转链表
定义一个函数,输入一个链表的头节点,反转该链表并输出反转后链表的头节点。
示例:
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL
限制:0 <= 节点个数 <= 5000
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode reverseList(ListNode head) {
//递归终止条件是当前为空,或者下一个节点为空
if(head == null || head.next == null){
return head;
}
//递归调用来反转每一个节点
ListNode cur = reverseList(head.next);
//每一个节点是怎么反转的
head.next.next = head;
//防止链表循环,需要将head.next设置为空
head.next = null;
//每层递归函数都返回cur也就是最后一个节点
return cur;
}
}
我们通过力扣上的题来再对递归思想和代码有个深入的了解
1. 首先找到递归的出口
就是找到链表最后一个节点(尾结点),我们要反转当前的链表,就必须从尾结点开始,因为链表的性质就是:通过头结点来找到后面的节点进行操作,CRUD都需要从头结点开始找。
找到当前链表的尾结点,就是反转链表的头结点(先不考虑头结点是否设立标兵)。
if(head == null || head.next == null)
这个条件对应两种情况:
当链表只有空结点时:
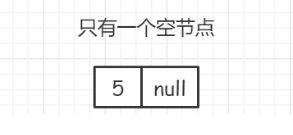
链表到尾结点时:
2. 递和归
为了形象的让大家理解这个过程,我们先以求阶乘为例:
注意点
递归函数必须要有终止条件,否则会出错;
递归函数先不断调用自身,直到遇到终止条件后进行回溯,最终返回答案
递操作:
那么针对此题中问题的拆分,我们可以这样:
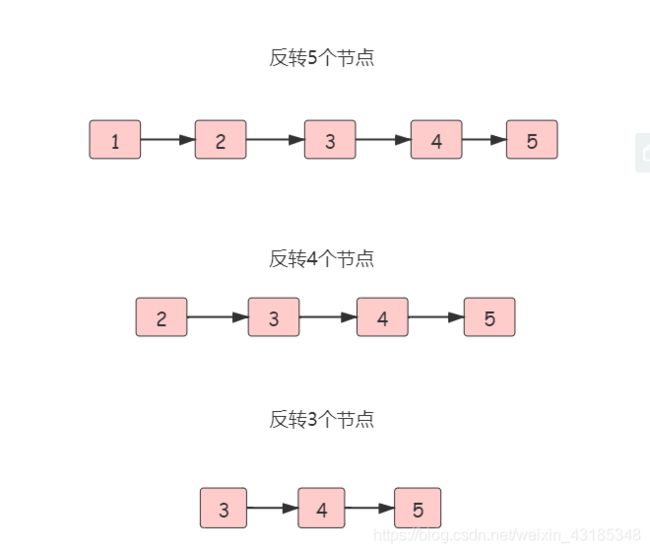
那最后剩余这个节点怎么办呀?
1这个节点是尾结点,它反转只要让它指向前驱节点即可
ListNode cur = reverseList(head.next);
cur是不变的,始终都等于1
真正完成节点反转的(就是节点间的指向发生改变的)是这句话:
head.next.next = head;
谁写的这句话,真的是太妙了
如果链表是 1 -> 2 -> 3 -> 4 -> 5,那么此时的cur就是5
而head是4,head的下一个是5,下下一个是空
所以head.next.next 就是4 -> 5
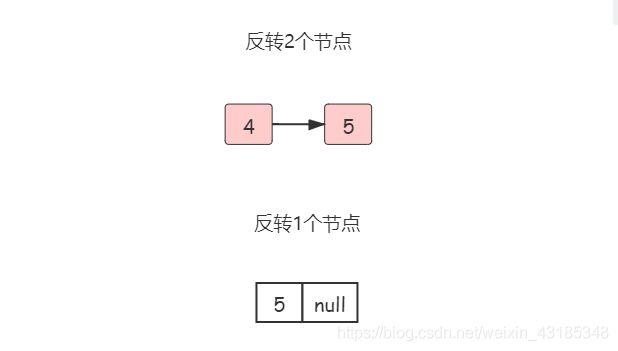
有一个小疑问就是:
head怎么就是4了?head作为头结点,一开始从尾结点反转时,应该是5呀!并且是怎么一步步来反转每一个节点呢?
这就是递归解法的精髓所在了。
首先经过上面的递操作之后,我们此时应该是这样的

此时head确实是5,满足了出口条件,变返回到了上一层,即有两个节点的情况。
由于是递归调用,head就向前走了一步,此时head==4
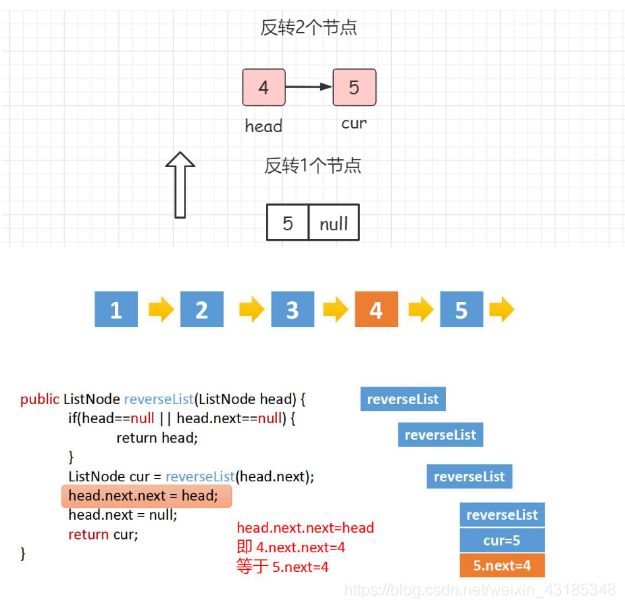
此时,head=4,head.next 是cur = 5,即head.next = cur = 5
我们要让cur指向head来反转,而不再指向为空
就是让cur.next = head = 4
消除中间等价量cur
那么就等价于head.next.next = head
面试题25. 合并两个排序的链表
输入两个递增排序的链表,合并这两个链表并使新链表中的节点仍然是递增排序的。
示例1:
输入:1->2->4, 1->3->4
输出:1->1->2->3->4->4
限制:0 <= 链表长度 <= 1000
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
ListNode dum = new ListNode(0);
ListNode cur = dum;
while(l1 != null && l2 != null){
if(l1.val >= l2.val){
cur.next = l2;
l2 = l2.next;
}else {
cur.next = l1;
l1 = l1.next;
}
cur = cur.next;
}
if(l2 == null) cur.next = l1;
if(l1 == null) cur.next = l2;
return dum.next;
}
}
面试题26. 树的子结构
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构, 即 A中有出现和B相同的结构和节点值。
例如:
给定的树 A:
3
/ \
4 5
/
1 2
给定的树 B:
4
/
1
返回 true,因为 B 与 A 的一个子树拥有相同的结构和节点值
示例 1:
输入:A = [1,2,3], B = [3,1]
输出:false
示例 2:
输入:A = [3,4,5,1,2], B = [4,1]
输出:true
限制:0 <= 节点个数 <= 10000
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public boolean isSubStructure(TreeNode A, TreeNode B) {
return (A != null && B != null)&&(recur(A,B)||isSubStructure(A.left, B)||isSubStructure(A.right, B));
}
public boolean recur(TreeNode A,TreeNode B){
if(B == null) return true;
if(A == null || A.val != B.val) return false;
return recur(A.left,B.left)&&recur(A.right,B.right);
}
}
面试题27. 二叉树的镜像
请完成一个函数,输入一个二叉树,该函数输出它的镜像。
例如输入:
4
/
2 7
/ \ /
1 3 6 9
镜像输出:
4
/
7 2
/ \ /
9 6 3 1
示例 1:
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode mirrorTree(TreeNode root) {
if(root == null) return null;
TreeNode temp = root.left;
root.left = mirrorTree(root.right);
root.right = mirrorTree(temp);
return root;
}
}
面试题28. 对称的二叉树
请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/
2 2
/ \ /
3 4 4 3
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1
/
2 2
\
3 3
示例 1:
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:
输入:root = [1,2,2,null,3,null,3]
输出:false
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public boolean isSymmetric(TreeNode root) {
if(root == null) return true;
return recur(root.left,root.right);
}
public boolean recur(TreeNode L,TreeNode R){
if(L == null && R == null) return true;
if(L == null || R == null || L.val != R.val) return false;
return recur(L.left, R.right) && recur(L.right, R.left);
}
}
面试题29. 顺时针打印矩阵
输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
示例 2:
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
限制:
0 <= matrix.length <= 100
0 <= matrix[i].length <= 100
可以将矩阵看成若干层,首先打印最外层的元素,其次打印次外层的元素,直到打印最内层的元素。
定义矩阵的第 kk 层是到最近边界距离为 kk 的所有顶点。例如,下图矩阵最外层元素都是第 11 层,次外层元素都是第 22 层,剩下的元素都是第 33 层。
class Solution {
public int[] spiralOrder(int[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return new int[0];
}
int rows = matrix.length, columns = matrix[0].length;
int[] order = new int[rows * columns];
int index = 0;
int left = 0, right = columns - 1, top = 0, bottom = rows - 1;
while (left <= right && top <= bottom) {
for (int column = left; column <= right; column++) {
order[index++] = matrix[top][column];
}
for (int row = top + 1; row <= bottom; row++) {
order[index++] = matrix[row][right];
}
if (left < right && top < bottom) {
for (int column = right - 1; column > left; column--) {
order[index++] = matrix[bottom][column];
}
for (int row = bottom; row > top; row--) {
order[index++] = matrix[row][left];
}
}
left++;
right--;
top++;
bottom--;
}
return order;
}
}
面试题30. 包含min函数的栈
定义栈的数据结构,请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中,调用 min、push 及 pop 的时间复杂度都是 O(1)。示例:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.min(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.min(); --> 返回 -2.
提示:
各函数的调用总次数不超过 20000 次
class MinStack {
Stack<Integer> A, B;
public MinStack() {
A = new Stack<>();
B = new Stack<>();
}
public void push(int x) {
A.push(x);
if(B.empty() || B.peek() >= x)
B.push(x);
}
public void pop() {
if(A.pop().equals(B.peek()))
B.pop();
}
public int top() {
return A.peek();
}
public int min() {
return B.peek();
}
}
/**
* Your MinStack object will be instantiated and called as such:
* MinStack obj = new MinStack();
* obj.push(x);
* obj.pop();
* int param_3 = obj.top();
* int param_4 = obj.min();
*/
面试题31. 栈的压入、弹出序列
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如,序列 {1,2,3,4,5} 是某栈的压栈序列,序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列,但 {4,3,5,1,2} 就不可能是该压栈序列的弹出序列。
示例 1:
输入:pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出:true
解释:我们可以按以下顺序执行:
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1
示例 2:
输入:pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出:false
解释:1 不能在 2 之前弹出。
提示:
0 <= pushed.length == popped.length <= 1000
0 <= pushed[i], popped[i] < 1000
pushed 是 popped 的排列。
class Solution {
public boolean validateStackSequences(int[] pushed, int[] popped) {
Stack<Integer> s =new Stack<>();
int i = 0;
for (Integer push : pushed) {
s.add(push);
while(!s.isEmpty() && s.peek() == popped[i]){
s.pop();
i++;
}
}
return s.isEmpty();
}
}
面试题32 - I. 从上到下打印二叉树
从上到下打印出二叉树的每个节点,同一层的节点按照从左到右的顺序打印。
例如:
给定二叉树: [3,9,20,null,null,15,7],
3
/
9 20
/
15 7
返回:
[3,9,20,15,7]
提示:
节点总数 <= 1000
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public int[] levelOrder(TreeNode root) {
if(root == null) return new int[0];
Queue<TreeNode> q = new LinkedList<>();
q.add(root);
ArrayList<Integer> arra = new ArrayList<>();
while(!q.isEmpty()){
TreeNode node = q.poll();
arra.add(node.val);
if(node.left != null)q.add(node.left);
if(node.right != null)q.add(node.right);
}
int[] res = new int[arra.size()];
for(int i = 0; i <= arra.size() - 1; i++){
res[i] = arra.get(i);
}
return res;
}
}
面试题32 - II. 从上到下打印二叉树 II
从上到下按层打印二叉树,同一层的节点按从左到右的顺序打印,每一层打印到一行。
例如:
给定二叉树: [3,9,20,null,null,15,7],
3
/
9 20
/
15 7
返回其层次遍历结果:
[
[3],
[9,20],
[15,7]
]
提示:
节点总数 <= 1000
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
Queue<TreeNode> q = new LinkedList<>();
if(root != null) q.add(root);
List<List<Integer>> arra = new ArrayList<>();
while(!q.isEmpty()){
List<Integer> temp = new ArrayList<>();
for(int j = q.size() - 1; j >= 0; j--){
TreeNode node = q.poll();
temp.add(node.val);
if(node.left != null)q.add(node.left);
if(node.right != null)q.add(node.right);
}
arra.add(temp);
}
return arra;
}
}
面试题32 - III. 从上到下打印二叉树 III
请实现一个函数按照之字形顺序打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右到左的顺序打印,第三行再按照从左到右的顺序打印,其他行以此类推。
例如:
给定二叉树: [3,9,20,null,null,15,7],
3
/
9 20
/
15 7
返回其层次遍历结果:
[
[3],
[20,9],
[15,7]
]
提示:
节点总数 <= 1000
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
Deque<TreeNode> q = new LinkedList<>();
if(root != null)q.add(root);
List<List<Integer>> arra = new ArrayList<>();
while(!q.isEmpty()){
List<Integer> temp = new ArrayList<>();
for(int j = q.size() - 1; j >= 0; j--){
TreeNode node = q.poll();
temp.add(node.val);
if(node.left != null)q.add(node.left);
if(node.right != null)q.add(node.right);
}
if(arra.size() % 2 == 1) Collections.reverse(temp);
arra.add(temp);
}
return arra;
}
}
面试题33. 二叉搜索树的后序遍历序列
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
参考以下这颗二叉搜索树:
5
/ \
2 6
/
1 3
示例 1:
输入: [1,6,3,2,5]
输出: false
示例 2:
输入: [1,3,2,6,5]
输出: true
提示:数组长度 <= 1000
class Solution {
public boolean verifyPostorder(int[] postorder) {
return recur(postorder,0,postorder.length - 1);
}
private boolean recur(int[] postorder, int i, int j) {
if(i > j)return true;
int p = i;
while(postorder[p] < postorder[j])p++;
int m = p;
while(postorder[p] > postorder[j])p++;
return (p == j)&&(recur(postorder,i,m-1))&&(recur(postorder,m,j - 1));
}
}
面试题34. 二叉树中和为某一值的路径
输入一棵二叉树和一个整数,打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ / \
7 2 5 1
返回:
[
[5,4,11,2],
[5,8,4,5]
]
提示:
节点总数 <= 10000
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
List<List<Integer>> res = new LinkedList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> pathSum(TreeNode root, int sum) {
recur(root,sum);
return res;
}
void recur(TreeNode root,int tar){
if(root == null)return;
path.add(root.val);
tar -= root.val;
if(tar == 0 && root.left == null && root.right == null){
res.add(new LinkedList(path));
}
recur(root.left, tar);
recur(root.right, tar);
path.removeLast();
}
}
面试题35. 复杂链表的复制
请实现 copyRandomList 函数,复制一个复杂链表。在复杂链表中,每个节点除了有一个 next 指针指向下一个节点,还有一个 random 指针指向链表中的任意节点或者 null。
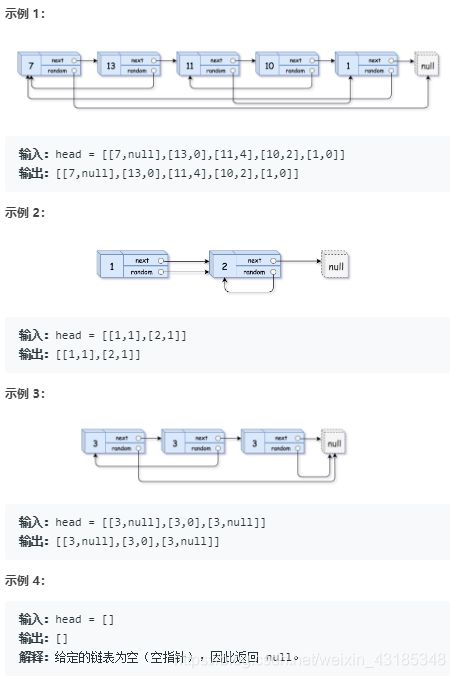
三步简单易懂
一、复制每一个节点,使得复制后的节点都在当前节点的下一个节点;
//拷贝链表
private void copy(Node head){
while(head!=null){
Node cloneNode = new Node(head.val);
Node nextNode = head.next;
head.next = cloneNode;
cloneNode.next = nextNode;
head = cloneNode.next;
}
}
二、原生链表的节点的指向任意节点,使复制的节点也都指向某一任意节点;
//指定随机指针
private void randomDirect(Node head){
while(head!=null){
Node cloneNode = head.next;
if(head.random!=null){
Node direct = head.random;
cloneNode.random = direct.next;
}
head = cloneNode.next;
}
}
三、重新连接节点,把原生节点重新连接起来,把克隆后的节点连接起来;
//重新连接 链表
private Node reList(Node head){
Node cloneNode = head.next;
Node cloneHead = cloneNode;
head.next = cloneNode.next;
head = head.next;
while(head!=null){
cloneNode.next = head.next;
head.next = head.next.next;
head = head.next;
cloneNode = cloneNode.next;
}
return cloneHead;
}
/*
// Definition for a Node.
class Node {
int val;
Node next;
Node random;
public Node(int val) {
this.val = val;
this.next = null;
this.random = null;
}
}
*/
class Solution {
public Node copyRandomList(Node head) {
if(head==null){
return null;
}
copy(head);
randomDirect(head);
return reList(head);
}
//拷贝链表
private void copy(Node head){
while(head!=null){
Node cloneNode = new Node(head.val);
Node nextNode = head.next;
head.next = cloneNode;
cloneNode.next = nextNode;
head = cloneNode.next;
}
}
//指定随机指针
private void randomDirect(Node head){
while(head!=null){
Node cloneNode = head.next;
if(head.random!=null){
Node direct = head.random;
cloneNode.random = direct.next;
}
head = cloneNode.next;
}
}
//重新连接 链表
private Node reList(Node head){
Node cloneNode = head.next;
Node cloneHead = cloneNode;
head.next = cloneNode.next;
head = head.next;
while(head!=null){
cloneNode.next = head.next;
head.next = head.next.next;
head = head.next;
cloneNode = cloneNode.next;
}
return cloneHead;
}
}
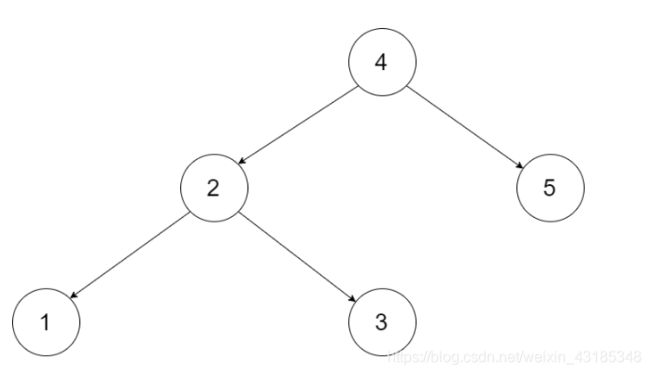
面试题36 二叉搜索树与双向链表
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。
为了让您更好地理解问题,以下面的二叉搜索树为例:
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。
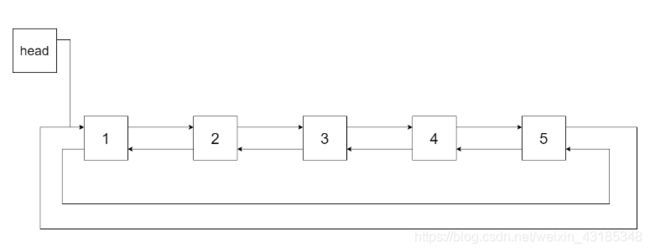
特别地,我们希望可以就地完成转换操作。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。
解题思路:
本文解法基于性质:二叉搜索树的中序遍历为 递增序列 。
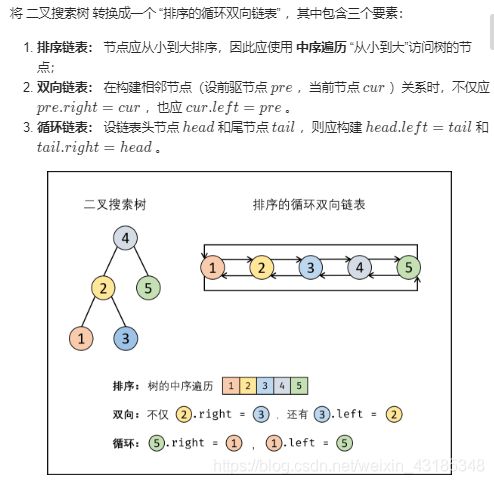
算法流程:

/*
// Definition for a Node.
class Node {
public int val;
public Node left;
public Node right;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val,Node _left,Node _right) {
val = _val;
left = _left;
right = _right;
}
};
*/
class Solution {
Node pre,head;
public Node treeToDoublyList(Node root) {
if(root == null) return null;
dfs(root);
//中序遍历树的节点,
pre.right = head;
head.left = pre;
//首位相连 构成双向循环链表
return head;
}
private void dfs(Node cur) {
if (cur == null) return;
dfs(cur.left);
if(pre != null)
pre.right = cur;
else
head = cur;
cur.left = pre;
pre = cur;
dfs(cur.right);
}
}
剑指 Offer 37. 序列化二叉树
请实现两个函数,分别用来序列化和反序列化二叉树。
示例:
你可以将以下二叉树:
1
/
2 3
/
4 5
序列化为 “[1,2,3,null,null,4,5]”
分析:层次遍历 广度优先 用队列
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Codec {
public String serialize(TreeNode root) {
if(root == null) return "[]";
StringBuilder res = new StringBuilder("[");
Queue<TreeNode> queue = new LinkedList<>() {{ add(root); }};
while(!queue.isEmpty()) {
TreeNode node = queue.poll();
if(node != null) {
res.append(node.val + ",");
queue.add(node.left);
queue.add(node.right);
}
else res.append("null,");
}
res.deleteCharAt(res.length() - 1);
res.append("]");
return res.toString();
}
public TreeNode deserialize(String data) {
if(data.equals("[]")) return null;
String[] vals = data.substring(1, data.length() - 1).split(",");
TreeNode root = new TreeNode(Integer.parseInt(vals[0]));
Queue<TreeNode> queue = new LinkedList<>() {{ add(root); }};
int i = 1;
while(!queue.isEmpty()) {
TreeNode node = queue.poll();
if(!vals[i].equals("null")) {
node.left = new TreeNode(Integer.parseInt(vals[i]));
queue.add(node.left);
}
i++;
if(!vals[i].equals("null")) {
node.right = new TreeNode(Integer.parseInt(vals[i]));
queue.add(node.right);
}
i++;
}
return root;
}
}
// Your Codec object will be instantiated and called as such:
// Codec codec = new Codec();
// codec.deserialize(codec.serialize(root));
牛逼写法
public class Codec {
private TreeNode root;
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
this.root =root;
return null;
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
return root;
}
}
面试题38. 字符串的排列
输入一个字符串,打印出该字符串中字符的所有排列。
你可以以任意顺序返回这个字符串数组,但里面不能有重复元素。
示例:
输入:s = “abc”
输出:[“abc”,“acb”,“bac”,“bca”,“cab”,“cba”]
限制:
class Solution {
List<String> res = new LinkedList<>();
char[] c;
public String[] permutation(String s) {
c = s.toCharArray();
dfs(0);
return res.toArray(new String[res.size()]);
}
void dfs(int x) {
if(x == c.length - 1) {
res.add(String.valueOf(c)); // 添加排列方案
return;
}
HashSet<Character> set = new HashSet<>();
for(int i = x; i < c.length; i++) {
if(set.contains(c[i])) continue; // 重复,因此剪枝
set.add(c[i]);
swap(i, x); // 交换,将 c[i] 固定在第 x 位
dfs(x + 1); // 开启固定第 x + 1 位字符
swap(i, x); // 恢复交换
}
}
void swap(int a, int b) {
char tmp = c[a];
c[a] = c[b];
c[b] = tmp;
}
}
面试题39. 数组中出现次数超过一半的数字
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入: [1, 2, 3, 2, 2, 2, 5, 4, 2]
输出: 2
class Solution {
public int majorityElement(int[] nums) {
int x = 0, votes = 0, count = 0;
//x代表元素,votes代表投票总数 count代表票数
for(int num : nums){
if(votes == 0)
x = num;
votes += num == x ? 1 : -1;
}
// 验证 x 是否为众数
for(int num : nums)
if(num == x)
count++;
return count > nums.length / 2 ? x : 0; // 当无众数时返回 0
}
}
面试题40. 最小的k个数
输入整数数组 arr ,找出其中最小的 k 个数。例如,输入4、5、1、6、2、7、3、8这8个数字,则最小的4个数字是1、2、3、4。
示例 1
输入:arr = [3,2,1], k = 2
输出:[1,2] 或者 [2,1]
示例 2:
输入:arr = [0,1,2,1], k = 1
输出:[0]
限制:
0 <= k <= arr.length <= 10000
0 <= arr[i] <= 10000
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
if(k >= arr.length)return arr;
int[] res = new int[k];
sort(arr);
for(int i = 0; i <= k - 1; i++){
res[i] = arr[i];
}
return res;
}
void sort(int[] arr){
for (int i = 0;i < arr.length;i++){
for(int j = i+1; j < arr.length;j++){
if(arr[i] > arr[j]){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
}
}
}
面试题41. 数据流中的中位数
如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。
例如,
[2,3,4] 的中位数是 3
[2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构:
void addNum(int num) - 从数据流中添加一个整数到数据结构中。
double findMedian() - 返回目前所有元素的中位数。
示例 1:
输入:
[“MedianFinder”,“addNum”,“addNum”,“findMedian”,“addNum”,“findMedian”]
[[],[1],[2],[],[3],[]]
输出:[null,null,null,1.50000,null,2.00000]
示例 2:
输入:
[“MedianFinder”,“addNum”,“findMedian”,“addNum”,“findMedian”]
[[],[2],[],[3],[]]
输出:[null,null,2.00000,null,2.50000]
限制:
最多会对 addNum、findMedia进行 50000 次调用
class MedianFinder {
Queue<Integer> A,B;
/** initialize your data structure here. */
public MedianFinder() {
A = new PriorityQueue<>();//小顶堆,保存较大的一半
B = new PriorityQueue<>((x,y)->(y - x));//大顶堆,保存较大的一半
}
public void addNum(int num) {
if(A.size() != B.size()){
A.add(num);
B.add(A.poll());
}else{
B.add(num);
A.add(B.poll());
}
}
public double findMedian() {
return A.size() != B.size()?A.peek():(A.peek()+B.peek())/2.0;
}
}
/**
* Your MedianFinder object will be instantiated and called as such:
* MedianFinder obj = new MedianFinder();
* obj.addNum(num);
* double param_2 = obj.findMedian();
*/
面试题42. 连续子数组的最大和
输入一个整型数组,数组里有正数也有负数。数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。
要求时间复杂度为O(n)。
示例1:
输入: nums = [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
提示:
1 <= arr.length <= 10^5
-100 <= arr[i] <= 100

class Solution {
public int maxSubArray(int[] nums) {
//对于每个数而言都有两种选择,要么接着左边的子数组继续,要么另起炉灶。
int res = nums[0];
for (int i = 1; i < nums.length; i++) {
nums[i] += Math.max(nums[i - 1], 0);
res = Math.max(res, nums[i]);
}
return res;
}
面试题43. 1~n整数中1出现的次数
输入一个整数 n ,求1~n这n个整数的十进制表示中1出现的次数。
例如,输入12,1~12这些整数中包含1 的数字有1、10、11和12,1一共出现了5次。
示例 1:
输入:n = 12
输出:5
示例 2:
输入:n = 13
输出:6
限制:
1 <= n < 2^31
class Solution {
public int countDigitOne(int n) {
int digit = 1, res = 0;
//digit代表位因子 res代表次数
int high = n / 10, cur = n % 10, low = 0;
//high代表当前位的高位 cur当前位 low低位
while(high != 0 || cur != 0) {
if(cur == 0) res += high * digit;
else if(cur == 1) res += high * digit + low + 1;
else res += (high + 1) * digit;
low += cur * digit;
cur = high % 10;
high /= 10;
digit *= 10;
}
return res;
}
}
面试题44. 数字序列中某一位的数字
数字以0123456789101112131415…的格式序列化到一个字符序列中。在这个序列中,第5位(从下标0开始计数)是5,第13位是1,第19位是4,等等。
请写一个函数,求任意第n位对应的数字。
示例 1:
输入:n = 3
输出:3
示例 2:
class Solution {
public int findNthDigit(int n) {
int digit = 1;//数位数 就是几位数
long start = 1;//每位数开始的数 比如 1 10 100
long count = 9;//每位数中 数字的个数
while (n > count) { // 1.确定在几位数中
n -= count;
digit += 1;
start *= 10;
count = digit * start * 9;
}
long num = start + (n - 1) / digit; // 2.确定digit位数中的第几位
return Long.toString(num).charAt((n - 1) % digit) - '0'; // 3.该数字中的第几位
}
}
面试题45. 把数组排成最小的数
输入一个非负整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。
示例 1:
输入: [10,2]
输出: “102”
示例 2:
输入: [3,30,34,5,9]
输出: “3033459”
提示:
0 < nums.length <= 100
说明:
输出结果可能非常大,所以你需要返回一个字符串而不是整数
拼接起来的数字可能会有前导 0,最后结果不需要去掉前导 0
class Solution {
public String minNumber(int[] nums) {
String[] strs = new String[nums.length];
for (int i = 0; i < nums.length; i++){
strs[i] = String.valueOf(nums[i]);
}
Arrays.sort(strs,(x,y)->(x + y).compareTo(y + x));
StringBuilder sb = new StringBuilder();
for (String string : strs) {
sb.append(string);
}
return sb.toString();
}
}
面试题46. 把数字翻译成字符串
给定一个数字,我们按照如下规则把它翻译为字符串:0 翻译成 “a” ,1 翻译成 “b”,……,11 翻译成 “l”,……,25 翻译成 “z”。一个数字可能有多个翻译。请编程实现一个函数,用来计算一个数字有多少种不同的翻译方法。
示例 1:
输入: 12258
输出: 5
解释: 12258有5种不同的翻译,分别是"bccfi", “bwfi”, “bczi”, “mcfi"和"mzi”
class Solution {
public int translateNum(int num) {
//a代表一个数字代表一个字母;b代表两个数字组成一个字母;
int a = 1, b = 1, x, y = num%10;
while(num != 0){
num/=10;
x = num % 10;
int temp = x * 10 + y;
int c = (temp >= 10 && temp <= 25)?a+b:a;
b = a;
a = c;
y = x;
}
return a;
}
}
面试题47. 礼物的最大价值
在一个 m*n 的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于 0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值,请计算你最多能拿到多少价值的礼物?
示例 1:
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物
提示:
0 < grid.length <= 200
0 < grid[0].length <= 200
class Solution {
public int maxValue(int[][] grid) {
int m = grid.length, n = grid[0].length;
for(int i = 0; i <= m -1; i++){
for(int j = 0; j <= n - 1; j++){
if(i == 0 && j == 0 )continue;
else if(i == 0)grid[i][j] += grid[i][j-1];
else if(j == 0)grid[i][j] += grid[i-1][j];
else grid[i][j] += Math.max(grid[i][j-1], grid[i-1][j]);
}
}
return grid[m - 1][n - 1];
}
}
面试题48. 最长不含重复字符的子字符串
请从字符串中找出一个最长的不包含重复字符的子字符串,计算该最长子字符串的长度。
示例 1:
输入: “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”,所以其长度为 3。
示例 2:
输入: “bbbbb”
输出: 1
解释: 因为无重复字符的最长子串是 “b”,所以其长度为 1。
示例 3:
输入: “pwwkew”
输出: 3
解释: 因为无重复字符的最长子串是 “wke”,所以其长度为 3。
请注意,你的答案必须是 子串 的长度,“pwke” 是一个子序列,不是子串。
思路:用双指针的差值作为最后的长度进行返回;初始化一个左指针i,有指针向前移动,
引入一个map记录每个字符和他的位置,乳沟字符重复,更新i值,则i到j的最大长度记为所求。
class Solution {
public int lengthOfLongestSubstring(String s) {
Map<Character,Integer> dic = new HashMap<>();
int i = -1, res = 0;
for(int j = 0; j < s.length(); j++){
if(dic.containsKey(s.charAt(j)))
//更新左指针
i = Math.max(i, dic.get(s.charAt(j)));
dic.put(s.charAt(j), j);
res = Math.max(res, j - i);
}
return res;
}
}
面试题Offor49 .丑数
我们把只包含因子 2、3 和 5 的数称作丑数(Ugly Number)。求按从小到大的顺序的第 n 个丑数。
示例:
输入: n = 10
输出: 12
解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。
说明:
1 是丑数。
n 不超过1690。
思路:找到这个最大小于n的丑数的序列,输出第n - 1位;
第一个丑数是1 接下来的就是 2的因子 3的因子 5的因子的最小值;
class Solution {
public int nthUglyNumber(int n) {
int p2 = 0, p3 = 0, p5 = 0;//定义三个指针,初始都为0位置
int[] res = new int[n];
res[0] = 1;
for(int i = 1; i < n; i++){
res[i] = Math.min(Math.min(res[p3]*3, res[p5]*5),2 * res[p2]);
//第一个丑数是1,计算第二个丑数,必须是2,3,5的倍数
if(res[i] == res[p2] * 2)p2++;
//找到归属2的倍数的下一个丑数
if(res[i] == res[p3] * 3)p3++;
//找到归属3的倍数的下一个丑数
if(res[i] == res[p5] * 5)p5++;
//找到归属5的倍数的下一个丑数
}
return res[n - 1];
//因为是从0开始的;所以第n位是res[n - 1]
}
}
面试题50. 第一个只出现一次的字符
在字符串 s 中找出第一个只出现一次的字符。如果没有,返回一个单空格。 s 只包含小写字母。
示例:
s = “abaccdeff”
返回 “b”
s = “”
返回 " "
思路: 二次遍历 ,
第一次找到重度的数字 第二次输出重度的数字
class Solution {
public char firstUniqChar(String s) {
char[] array = s.toCharArray();
Map<Character,Boolean> map = new HashMap<>();
for (char c : array) {
map.put(c,!map.containsKey(c));
}
for (char c : array) {
if(map.get(c))return c;
}
return ' ';
}
}
面试题51. 数组中的逆序对
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
示例 1:
输入: [7,5,6,4]
输出: 5
public class Solution {
public int reversePairs(int[] nums) {
int len = nums.length;
if (len < 2) {
return 0;
}
int[] copy = new int[len];
for (int i = 0; i < len; i++) {
copy[i] = nums[i];
}
int[] temp = new int[len];
return reversePairs(copy, 0, len - 1, temp);
}
/**
* nums[left..right] 计算逆序对个数并且排序
*
* @param nums
* @param left
* @param right
* @param temp
* @return
*/
private int reversePairs(int[] nums, int left, int right, int[] temp) {
if (left == right) {
return 0;
}
int mid = left + (right - left) / 2;
int leftPairs = reversePairs(nums, left, mid, temp);
int rightPairs = reversePairs(nums, mid + 1, right, temp);
if (nums[mid] <= nums[mid + 1]) {
return leftPairs + rightPairs;
}
int crossPairs = mergeAndCount(nums, left, mid, right, temp);
return leftPairs + rightPairs + crossPairs;
}
/**
* nums[left..mid] 有序,nums[mid + 1..right] 有序
*
* @param nums
* @param left
* @param mid
* @param right
* @param temp
* @return
*/
private int mergeAndCount(int[] nums, int left, int mid, int right, int[] temp) {
for (int i = left; i <= right; i++) {
temp[i] = nums[i];
}
int i = left;
int j = mid + 1;
int count = 0;
for (int k = left; k <= right; k++) {
if (i == mid + 1) {
nums[k] = temp[j];
j++;
} else if (j == right + 1) {
nums[k] = temp[i];
i++;
} else if (temp[i] <= temp[j]) {
nums[k] = temp[i];
i++;
} else {
nums[k] = temp[j];
j++;
count += (mid - i + 1);
}
}
return count;
}
}
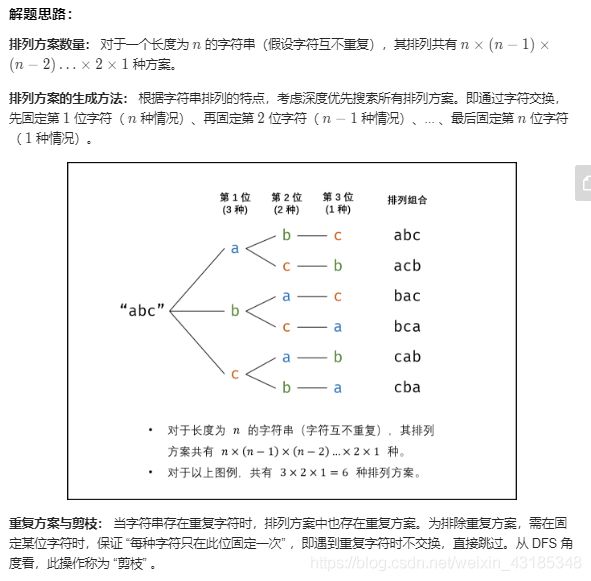
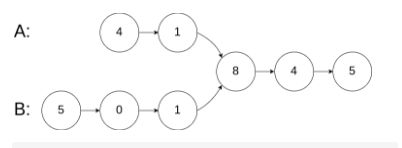
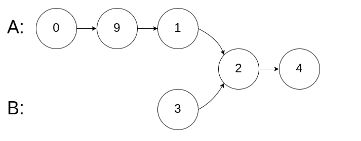
面试题52. 两个链表的第一个公共节点
输入两个链表,找出它们的第一个公共节点。
如下面的两个链表:
在节点 c1 开始相交。
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出:Reference of the node with value = 8
输入解释:相交节点的值为 8 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
示例 2:
输入:intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Reference of the node with value = 2
输入解释:相交节点的值为 2 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [0,9,1,2,4],链表 B 为 [3,2,4]。在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:null
输入解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
解释:这两个链表不相交,因此返回 null。
注意:
如果两个链表没有交点,返回 null.
在返回结果后,两个链表仍须保持原有的结构。
可假定整个链表结构中没有循环。
程序尽量满足 O(n) 时间复杂度,且仅用 O(1) 内存。
思路:两个链表同时指向下一位 相等则返回
哈哈
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
ListNode node1 = headA,node2 = headB;
while(node1 != node2){
node1 = node1 == null?headB:node1.next;
node2 = node2 == null?headA:node2.next;
}
return node1;
}
}
面试题53 - II. 0~n-1中缺失的数字
一个长度为n-1的递增排序数组中的所有数字都是唯一的,并且每个数字都在范围0~n-1之内。在范围0~n-1内的n个数字中有且只有一个数字不在该数组中,请找出这个数字。
示例 1:
输入: [0,1,3]
输出: 2
示例 2:
输入: [0,1,2,3,4,5,6,7,9]
输出: 8
class Solution {
public int missingNumber(int[] nums) {
for(int i = 0; i < nums.length; i++){
if(i != nums[i])return i;
}
return nums.length;
}
}