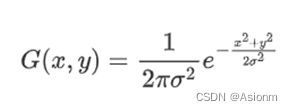计算机视觉实验:图像增强应用实践
本次实验主要从基于统计、函数映射的图像增强方法和基于滤波的图像增强方法两种方法中对一些图像增强的算法进行实现。主要的编程语言为python,调用了python自带的PIL图像库用于读取图像,利用numpy进行图像运算,最后使用opencv第三方库进行对比验证。下面为实验的详细步骤与过程。
基于统计、函数映射的图像增强方法
图像反转
所谓的图像反转是将颜色或灰度进行颠倒,如白色变成黑色,亮变暗暗变亮等等。其原理在于用255减去每个像素的颜色值或灰度值,从而达到反转的效果,R/G/B = 255 - R/G/B。下面使用代码进行实现(完整代码见 图片反转.py)。
- 调用Image与numpy读取图像信息
- img = np.array(Image.open(path))
- 根据shape判断是否是彩色图并用255减去颜色值
- if len(img.shape) > 2:
- img = np.array(list(map(lambda x:list(map(lambda y:list(map(lambda z:255-z, y)), x)), img)))
- else:
- img = np.array(list(map(lambda x:list(map(lambda y:255-y, x)) , img)))
- 保存图像
- # 下面的uint8是为了改变数据类型 否则会报错
- image = Image.fromarray(np.uint8(img))
- # 保存图片
- image.save(f'./output/reverse/{path[7:]}')
- image.show()
调用opencv进行结果对比
代码如下所示,此代码调用了opencv库进行图像反转操作。完整代码见图片反转opencv.py
与上面的代码基本一致,不同点在于调用Opencv来代替Image与numpy的部分操作。其关键不同代码如下所示。
- # 创建空图像
- dst = np.zeros((height, width, 3), np.uint8)
- for i in range(height):
- for j in range(width):
- (b, g, r) = img[i, j]
- b = 255 - b
- g = 255 - g
- r = 255 - r
- dst[i, j] = (b, g, r)
- # 部分代码参考于https://laoai.blog.csdn.net/article/details/81133070
最后两者结果如下图图1所示
| 图1 图像反转结果对比图 |
从结果中可以看出,与原始图像相比颜色发生了很大的反转。而未用Openvc处理与使用了Opencv处理的结果是一样的。
直方图均衡化
直方图均衡化只要是让灰度能均匀分布而不是集中在某个范围内。使得某些地方特别亮某些特别暗。直方图均衡化的操作流程一般如下图图2所示,首先需要计算出目前原始图像的灰度直方图。然后对数量占比进行累加。累加得到的结果均在0-1之间。那么用255乘以结果,以获取最新的映射关系,此时再绘制直方图那么就可看出其分布更均匀。下面利用代码进行实现。
| 图2 直方图均衡化流程图 |
此处使用一张灰度图进行处理coins.png。
- 计算直方图
利用字典统计每个灰度值的数量映射
- def show_hist(img):
- hist = collections.defaultdict(int)
- for i in img:
- for j in i:
- hist[j] += 1
- # 绘制直方图
- plt.title('灰度直方图')
- plt.xlabel('Bins')
- plt.xlim([0, 256])
- plt.ylabel('Pixels')
- plt.bar(hist.keys(), hist.values())
- plt.show()
- return hist
累加操作
- for i in range(256):
- if i:
- reduction_hist[i] = hist[i]+reduction_hist[i-1]
- else:
- reduction_hist[i] = hist[i]
- 计算新的映射关系
- for index, i in enumerate(img):
- for jndex, j in enumerate(i):
- img[index][jndex] = reduction_hist[img[index][jndex]]*255
调用opencv进行结果对比
Opencv只需要调用下面的库函数即可进行直方图均衡化操作。详细代码可见直方图均衡化cv.py
- img = cv2.equalizeHist(img)
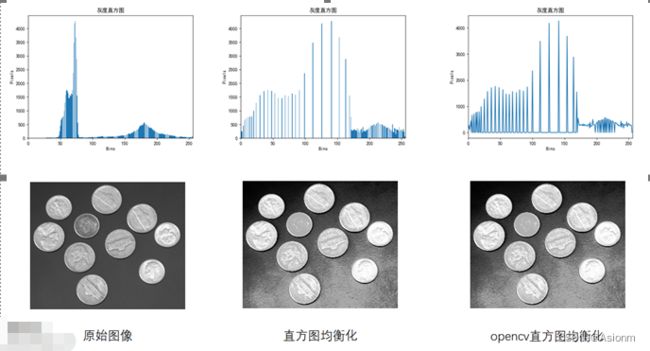
将原始图像、非opencv处理的直方图均衡化图像与opencv处理的直方图均衡化图像进行对比,如下图图3所示。可以看到后面两者与前面原始图像相比其直方图分布更均匀。而后面两者基本无差别。
| 图3 直方图均衡化结果对比图 |
伽马变换
伽马变换的数学公式如下所示,其中s为变换后的值,c为一常数此处取1,$\gamma$是用于控制变换幅度的,而r则是原图像的输入范围在0-1。
在查阅资料后发现,opencv并未自带伽马变换的相关函数,所以此处不进行与opencv的结果对比。根据学习发现,伽马变换需要进行以下步骤。
- 图像数据归一化
- 图像各像素点进行乘幂运算
最后代码如下:
- def gama_transfer(img,power1):
- if len(img.shape) > 3:
- img = cv2.cvtColor(img,cv2.COLOR_BGR2RGB)
- img = 255*np.power(img/255,power1)
- img = np.around(img)
- img[img>255] = 255
- out_img = img.astype(np.uint8)
- return out_img
- # 参考于https://zhuanlan.zhihu.com/p/340513008?utm_id=0
结果输出如下图图4所示,
| 图4 伽马变换结果对比图 |
从图片对比中可以看出, 时暗部变量,对于此图可以看得更清晰, 时暗部变暗,图片则更难看清。
基于滤波的图像增强方法
均值滤波
均值滤波的原理在于将图像中的每个像素点的值都变成其周围n阶矩阵的平均值。所以在编程实现中,首先需要创建一个大小一样的0矩阵用以记录平均值。然后遍历一次图像,将计算得到的平均值填充进0矩阵中即可得到均值滤波的结果。其核心代码如下(完整可见`均值滤波.py`):
- for index in range(height):
- for jndex in range(width):
- # 判断是否为边界
- if index <= int((kernel-1)/2) - 1 or index >= height - 1 - int((kernel-1)/2) \
- or jndex <= int((kernel-1)/2) - 1 or jndex >= height - int((kernel-1)/2) - 1:
- result[index, jndex] = img[index, jndex]
- else: # 均值值滤波
- result[index, jndex] = np.average(
- img[index - int((kernel-1)/2):index + int((kernel-1)/2) + 1,
- jndex - int((kernel-1)/2):jndex + int((kernel-1)/2) + 1])
- # 部分参考于https://blog.csdn.net/qq_43633939/article/details/120854570
此处对于边界不做任何处理。上面的代码是针对灰度图的,若需要对彩色图片进行滤波处理,则可在后面加上三个通道即可如下面代码所示。
- for kndex in range(3):
- result[index, jndex, kndex] = np.average(
- img[index - int((kernel - 1) / 2):index + int((kernel - 1) / 2) + 1,
- jndex - int((kernel - 1) / 2):jndex + int((kernel - 1) / 2) + 1, kndex])
调用opencv进行结果对比
均值滤波对于opencv存在一个函数调用,只需要指定滤波核即可进行操作。此处滤波核均选择3*3。
- import cv2
- path = './pics/save.bmp'
- # img = cv2.imread(path, cv2.IMREAD_GRAYSCALE)
- img = cv2.imread(path)
- ksize = [3,3]
- dst=cv2.blur(img,ksize)
- cv2.imshow('img', dst)
- cv2.imwrite(f'./cv-output/mean-filtering/{path[7:]}', img)
- cv2.waitKey(0)
最后将输出结果进行对比,如下图图5所示。
| 图5 均值滤波结果对比图 |
可以看出原图和滤波后的图像差别还是很大的,原图的噪点颗粒很清晰,而滤波后则变得模糊。同时opencv的结果和自编代码的结果差别不大。
高斯滤波
高斯滤波的流程图如下图图6所示,
| 图6 高斯滤波流程图 |
对于高斯滤波首先需要根据下面的高斯公式计算出各点的高斯值,
其中x,y均是离中心点的距离,所以说对于整个图像高斯值是固定的。在得到这些值后,将他们的各自除以他们的和以进行归一化。最后中心值等于归一化的结果除以周围点颜色值后求和。根据以上思路可进行编程如下:
- 计算高斯值
- kernel = 3
- sigma = 1.3
- K = np.zeros([kernel, kernel])
- # 计算高斯值
- for x in range(-1, 2):
- for y in range(-1,2):
- K[x+1, y+1] = np.exp( -(x ** 2 + y ** 2) / (2 * (sigma ** 2)))
- 归一化
- # 归一化
- K = K/np.sum(K)
- 加权求和
- result[index, jndex] = np.sum(K*img[index - int((kernel-1)/2):index + int((kernel-1)/2) + 1,
- jndex - int((kernel-1)/2):jndex + int((kernel-1)/2) + 1])
完整代码可见于`高斯滤波.py`
调用opencv进行结果对比
对于opencv高斯滤波只需要一个函数即可进行。完整代码见高斯滤波cv.py。
- result = cv2.GaussianBlur(img, (3, 3), 1.3)
最后输出结果如下图图7所示,
| 图7 高斯滤波结果对比图 |
可以看到和原图相比高斯滤波后的结果变得模糊,同时有些噪点也变得不明显。高斯滤波的结果和opencv的结果基本一致。
实验结论或体会
本次实验完成了图像反转、直方图均衡化、伽马变换、均值滤波、高斯滤波五种图像增强方法的代码实现。并将输出的图片与opencv的结果进行对比发现基本一致,说明本次实验编程实现的方法基本与实际相符合。同时图像增强后的图像与原图进行对比,可以看出不同增强方法的作用,比如说高斯滤波可以减弱图像的噪点,伽马变换可以让原图的暗部或亮部细节更突出以获得隐藏的信息,直方图均衡化可以让图像亮度或颜色分布更均匀使得图像原本不能看出的细节可清晰显示等等。
在此次实验中,对图像进行增强需要用到python的PIL库和numpy库,这些的使用让我们更加地了解图像处理的方式。同时通过对这些库的练习也让我更加熟练地直接操作图像的像素点。理论课中讲解的关于图像增强方法的知识,在代码编辑实现过程中均得以体现,通过实验对理论知识理解也更加深入。总而言之,此次的实验让我对图像增强方法以及图像的处理方法有了更加深入的了解。