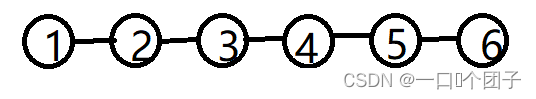数据结构与算法（一）

之前一直都在给大家更新C语言的一些学习心得，接下来呢，也会带着大家在有一些C/C++语言的基础之上，浅浅自学一下数据结构与算法，可能会存在很多不足之处。还望大家在评论区互动、指正。

一.对数据结构与算法的认识

1.数据结构与算法的重要性

凭借一句话获得图灵奖的Pascal语言之父–Nicklaus Wirth,让他获得图灵奖的这句话就是他提出的著名公式–“程序 = 数据结构 + 算法”，这个公式对计算机科学的影响程度足以类似于物理学中爱因斯坦的“E = MC^2”。这一个公式就展示了程序的本质，想要写出好的程序，那么必然要懂得数据结构和算法！数据结构是计算机软件相关专业的专业基础课，非常重要，在此基础上能够更好的学好数据库、操作系统、编译原理等专业课程。它在计算机相关专业的教学课程中处于一个承上启下的核心地位，并且它是介于数学、计算机硬件和计算机软件三者之间的一门核心课程。

2.数据结构与算法都学些什么？

章节	内容
1	数据结构绪论
2	算法
3	线性表
4	栈与队列
5	串
6	树
7	图
8	查找
9	排序

以上是我参考数据结构相关书本总结，如有不足，欢迎大家补充！

3.数据结构与算法好学吗？

根据之前的初识，可以总结为以下几点：

• 概念性强
• 算法灵活、不易掌握
• 逻辑性强，算法设计很烧脑

综上，这门课程的难度还是相当大的！我们大家一起努力，多看看书，多做题，好好思考。

二.绪论

1.数据结构的研究内容

通常，我们用计算机解决一个问题的步骤大致如下：先将具体问题抽象为数学模型，然后设计算法，最后编程、调试、运行。具体问题抽象为数学模型的实质就是分析问题-提取操作对象-找出操作对象之间的关系-用数学语言来描述。这里操作对象以及操作对象之间的关系就是所谓的数据结构。数据结构是相互之间存在一种或者多种特定关系的数据元素的集合。

2.基本概念和术语

说到数据结构，我们先谈一谈什么是数据呢？

2.1数据

数据：是描述客观事物的符号，是计算机中可以操作的对象，是能被计算机识别，并输入给计算机处理的符号集合。数据不仅仅包括整型等数值类型，还包括字符及声音、图像、视频等非数值类型。

2.2数据元素

数据元素：是组成数据的、有一定意义的基本单位，在计算机中通常作为整体处理，也被称为记录、结点或者顶点。比如，在人类中，什么是数据元素？当然是人！

2.3数据项

数据项是构成数据元素的不可分割的最小单位。一个数据元素可以由若干个数据项组成。

• 数据、数据元素、数据项三者之间的关系：数据>数据元素>数据项

2.4数据对象

数据对象：是性质相同的数据元素的集合，是数据的子集。

例如：整数数据对象的集合是集合N={0,1,-1,2,-2…}

说了数据的定义，那么数据结构中的结构又是什么呢？

2.5数据结构

结构，简单的理解就是关系，比如分子结构，就是说组成分子的原子之间的排列方式。数据元素不是孤立存在的，它们之间存在着某种关系，数据元素相互之间的关系称为结构。因此，数据结构就是指相互之间存在着一种或多种特定关系的数据元素集合。

数据结构包含以下三个方面内容：

• 数据元素之间的逻辑关系，也称逻辑结构。
• 数据元素及其关系在计算机内存中的表示（又称映像），称为数据的物理结构或数据的存储结构。
• 数据的运算和实现，即对数据元素可以施加的操作以及这些操作在相应的存储结构上的实现。

2.5.1逻辑结构

逻辑结构：是指数据对象中的数据元素之间的相互关系。

它与数据的存储无关，独立于计算机。它是从具体的问题抽象出来的数学模型。

2.5.1.1集合结构

集合结构：集合结构中的数据元素除了同属于一个集合外，它们之间没有其他关系。

集合结构也类似于数学中的集合：

2.5.1.2线性结构

线性结构：线性结构中的数据元素之间是一对一的关系。

关于线性结构，可以想象成糖葫芦的样子：

2.5.1.3树形结构

树形结构：树形结构中的数据元素之间存在一种一对多的关系

简单示意图如下：

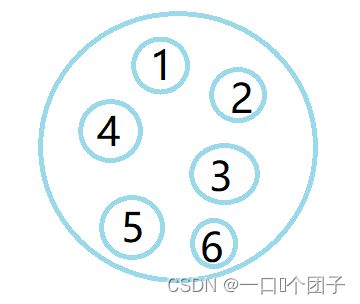
2.5.1.4图形结构

图形结构：图形结构的数据元素是多对多的关系。

示意图如下：

我们在用示意图表示数据的逻辑结构时，需要注意两点：

1. 将每个数据元素看作一个结点，用圆圈表示。
2. 元素之间的逻辑关系用结点之间的连线表示，如果这个关系是有方向的，那么用带箭头的连线表示。

2.5.2物理结构（存储结构）

物理结构：是指数据的逻辑结构在计算机中的存储形式。

四种基本的存储结构：

• 顺序存储结构
• 链式存储结构
• 索引存储结构
• 散列存储结构

2.5.2.1顺序存储结构

顺序存储结构：是把数据元素存放在地址连续的存储单元里，其数据间的逻辑关系和物理关系是一致的。

这种存储结构其实很简单，就是占位排队的意思，数组就是这样的存储方式，当你告诉计算机想要建立一个9个整形数据的数组，计算机就会在内存中开辟一片空地，按照一个整形所占位置的大小乘以9，开辟连续的空间，于是第一个元素就放在第一个位置，以此类推。

2.5.2.2链式存储结构

链式存储结构：是把数据元素存放在任意的存储单元里，这组存储单元可以是连续的，也可以是不连续的。

数据元素的存储关系并不能反映其逻辑关系，因此需要一个指针存放数据元素的地址，这样可以通过指针就可以找到相关数据元素的位置。

2.5.2.3索引存储结构

可以简单的类比通论录来理解。

• 在存储结点信息的同时，还建立附加的索引表。
• 索引表的每一项称为一个索引项。
• 索引项的一般形式：（关键字，地址）
• 关键字是能唯一标识一个结点的那些数据项。
• 若每个结点在索引表中都有一个索引项，则该索引表称之为稠密索引。若一组结点在索引表中只对应一个索引项，则该索引表称之为稀疏索引。

2.5.2.4散列存储结构

• 根据结点的关键字直接计算出该结点的存储地址。

逻辑结构是面向问题的，而物理结构是面向计算机的，其基本目标就是将数据及其逻辑关系存储到计算机的内存中。

• 逻辑结构与物理结构的关系：
  1.物理结构是逻辑关系的映象与元素本身的映象。
  2.逻辑结构是数据结构的抽象，物理结构是数据结构的实现。
  两者综合起来就建立起了数据元素之间的结构关系。

2.6数据类型

数据类型：是指一组性质相同的值的集合及定义在此集合上的一些操作的总称。

数据类型是按值的不同进行划分的。在高级语言中，每个变量、常量和表达式都有各自的取值范围。类型就用来说明变量或表达式的取值范围和所能进行的操作。
在C语言中，按照取值的不同，数据类型可以分为两类：

• 原子类型：是不可以再分解的基本类型，包括整型、实型、字符型等
• 结构类型：有若干个类型组合而成，是可以再分解的。比如，整型数组由若干个整型数据组成。

比如：在C语言中声明变量int a 和b,就意味着，在给变量a和b赋值时不能超出int的取值范围，变量a和b之间的运算只能在int类型所允许的运算。

2.6.1抽象数据类型

抽象是指抽取出事物所具有的普遍性的本质。
如下图所示：

如果我问你，你在上图中看到了什么？那么我相信大家的回答一定是圆，忽略了它们的颜色和大小，它们的本质为圆，这就是抽象。

抽象数据类型（Abstract Data Type,ADT）：一个数学模型及定义在该模型上的一组操作。

• 由用户定义，从问题抽象出数据模型（逻辑结构）
• 还包括定义在数据模型上的一组抽象运算
• 不考虑计算机内的具体存储结构与运算的具体实现算法

这里我们给出抽象数据类型的定义格式：
ADT 抽象数据类型名
{
数据对象:<数据对象的定义>
数据关系:<数据关系的定义>
基本操作:<基本操作的定义>
}ADT 抽象数据类型名

其中：数据对象、数据关系的定义用伪代码描述。

• 基本操作定义格式：
• 基本操作名(参数表)
• 初始条件:<初始条件描述>
• 操作结果:<操作结果描述>

基本操作定义格式说明：
1.参数表:赋值参数只为操作提供输入值，引用参数以&打头，除可提供输入值外，还将返回操作结果。
2.初始条件:描述操作执行之前数据结构和参数应满足的条件，若不满足，则操作失败，并返回相应出错信息。若初始条件为空，则省略之。
3.操作结果:说明操作正常完成之后，数据结构的变化状况和应返回的结果。

下面给出抽象数据类型定义举例：Circle的定义

ADT Circle
{
数据类型:D={r,x,y|r,x,y均为实数}
数据关系:R={|r是半径,是圆心坐标}
基本操作:
Circle(&C,r,x,y)
操作结果:构造一个圆。
double Area( C )
初始条件:圆已存在
操作结果：计算面积
…
}ADT Circle

2.6.1.1抽象数据类型的实现

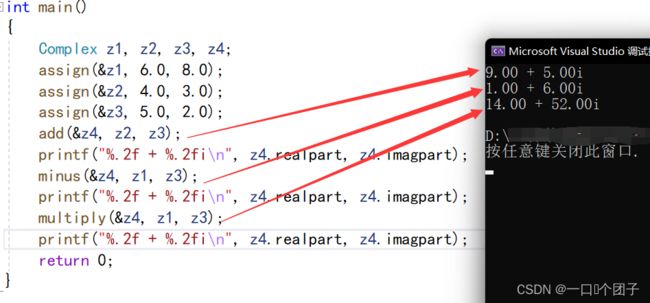
C语言实现抽象数据类型：用已有数据类型定义描述它的存储结构，用函数定义描述它的操作。
例如：抽象数据类型复数的实现

#define _CRT_SECURE_NO_WARNINGS 1
#include 
typedef struct Complex
{
	float realpart;//实部
	float imagpart;//虚部
}Complex;
void assign(Complex* A, float real, float imag);//赋值
void add(Complex* C, Complex A, Complex B);//加法
void minus(Complex* C, Complex A, Complex B);//减法
void multiply(Complex* C, Complex A, Complex B);//乘法
void assign(Complex* A, float real, float imag)
{
	A->realpart = real;//实部赋值
	A->imagpart = imag;//虚部赋值
}
void add(Complex* C, Complex A,Complex B)
{
	C->imagpart = A.imagpart + B.imagpart;
	C->realpart = A.realpart + B.realpart;
}
void minus(Complex* C, Complex A, Complex B)
{
	C->imagpart = A.imagpart - B.imagpart;
	C->realpart = A.realpart - B.realpart;
}
void multiply(Complex* C, Complex A, Complex B)
{
	C->imagpart = A.realpart * B.imagpart + A.imagpart * B.realpart;
	C->realpart = A.realpart * B.realpart - A.imagpart * B.imagpart;
}
int main()
{
	Complex z1, z2, z3, z4;
	assign(&z1, 6.0, 8.0);
	assign(&z2, 4.0, 3.0);
	assign(&z3, 5.0, 2.0);
	add(&z4, z2, z3);
	printf("%.2f + %.2fi\n", z4.realpart, z4.imagpart);
	minus(&z4, z1, z3);
	printf("%.2f + %.2fi\n", z4.realpart, z4.imagpart);
	multiply(&z4, z1, z3);
	printf("%.2f + %.2fi\n", z4.realpart, z4.imagpart);
	return 0;
}

好啦，今天就学到这里啦，欢迎大家关注、点赞和评论！