Want595

【Python机器学习】实验04(1) 多分类(基于逻辑回归)实践

文章目录

多分类以及机器学习实践
- 如何对多个类别进行分类
- - 1.1 数据的预处理
  - 1.2 训练数据的准备
  - 1.3 定义假设函数，代价函数，梯度下降算法（从实验3复制过来）
  - 1.4 调用梯度下降算法来学习三个分类模型的参数
  - 1.5 利用模型进行预测
  - 1.6 评估模型
  - 1.7 试试sklearn
- 实验4(1) 请动手完成你们第一个多分类问题，祝好运！完成下面代码
- - 2.1 数据读取
  - 2.2 训练数据的准备
  - 2.3 定义假设函数、代价函数和梯度下降算法
  - 2.4 学习这四个分类模型
  - 2.5 利用模型进行预测
  - 2.6 计算准确率

多分类以及机器学习实践

如何对多个类别进行分类

Iris数据集是常用的分类实验数据集，由Fisher, 1936收集整理。Iris也称鸢尾花卉数据集，是一类多重变量分析的数据集。数据集包含150个数据样本，分为3类，每类50个数据，每个数据包含4个属性。可通过花萼长度，花萼宽度，花瓣长度，花瓣宽度4个属性预测鸢尾花卉属于（Setosa，Versicolour，Virginica）三个种类中的哪一类。

iris以鸢尾花的特征作为数据来源，常用在分类操作中。该数据集由3种不同类型的鸢尾花的各50个样本数据构成。其中的一个种类与另外两个种类是线性可分离的，后两个种类是非线性可分离的。

该数据集包含了4个属性：
Sepal.Length（花萼长度），单位是cm;
Sepal.Width（花萼宽度），单位是cm;
Petal.Length（花瓣长度），单位是cm;
Petal.Width（花瓣宽度），单位是cm;

种类：Iris Setosa（山鸢尾）、Iris Versicolour（杂色鸢尾），以及Iris Virginica（维吉尼亚鸢尾）。

1.1 数据的预处理

import sklearn.datasets as datasets
import pandas as pd
import numpy as np

data=datasets.load_iris()
data

{'data': array([[5.1, 3.5, 1.4, 0.2],
        [4.9, 3. , 1.4, 0.2],
        [4.7, 3.2, 1.3, 0.2],
        [4.6, 3.1, 1.5, 0.2],
        [5. , 3.6, 1.4, 0.2],
        [5.4, 3.9, 1.7, 0.4],
        [4.6, 3.4, 1.4, 0.3],
        [5. , 3.4, 1.5, 0.2],
        [4.4, 2.9, 1.4, 0.2],
        [4.9, 3.1, 1.5, 0.1],
        [5.4, 3.7, 1.5, 0.2],
        [4.8, 3.4, 1.6, 0.2],
        [4.8, 3. , 1.4, 0.1],
        [4.3, 3. , 1.1, 0.1],
        [5.8, 4. , 1.2, 0.2],
        [5.7, 4.4, 1.5, 0.4],
        [5.4, 3.9, 1.3, 0.4],
        [5.1, 3.5, 1.4, 0.3],
        [5.7, 3.8, 1.7, 0.3],
        [5.1, 3.8, 1.5, 0.3],
        [5.4, 3.4, 1.7, 0.2],
        [5.1, 3.7, 1.5, 0.4],
        [4.6, 3.6, 1. , 0.2],
        [5.1, 3.3, 1.7, 0.5],
        [4.8, 3.4, 1.9, 0.2],
        [5. , 3. , 1.6, 0.2],
        [5. , 3.4, 1.6, 0.4],
        [5.2, 3.5, 1.5, 0.2],
        [5.2, 3.4, 1.4, 0.2],
        [4.7, 3.2, 1.6, 0.2],
        [4.8, 3.1, 1.6, 0.2],
        [5.4, 3.4, 1.5, 0.4],
        [5.2, 4.1, 1.5, 0.1],
        [5.5, 4.2, 1.4, 0.2],
        [4.9, 3.1, 1.5, 0.2],
        [5. , 3.2, 1.2, 0.2],
        [5.5, 3.5, 1.3, 0.2],
        [4.9, 3.6, 1.4, 0.1],
        [4.4, 3. , 1.3, 0.2],
        [5.1, 3.4, 1.5, 0.2],
        [5. , 3.5, 1.3, 0.3],
        [4.5, 2.3, 1.3, 0.3],
        [4.4, 3.2, 1.3, 0.2],
        [5. , 3.5, 1.6, 0.6],
        [5.1, 3.8, 1.9, 0.4],
        [4.8, 3. , 1.4, 0.3],
        [5.1, 3.8, 1.6, 0.2],
        [4.6, 3.2, 1.4, 0.2],
        [5.3, 3.7, 1.5, 0.2],
        [5. , 3.3, 1.4, 0.2],
        [7. , 3.2, 4.7, 1.4],
        [6.4, 3.2, 4.5, 1.5],
        [6.9, 3.1, 4.9, 1.5],
        [5.5, 2.3, 4. , 1.3],
        [6.5, 2.8, 4.6, 1.5],
        [5.7, 2.8, 4.5, 1.3],
        [6.3, 3.3, 4.7, 1.6],
        [4.9, 2.4, 3.3, 1. ],
        [6.6, 2.9, 4.6, 1.3],
        [5.2, 2.7, 3.9, 1.4],
        [5. , 2. , 3.5, 1. ],
        [5.9, 3. , 4.2, 1.5],
        [6. , 2.2, 4. , 1. ],
        [6.1, 2.9, 4.7, 1.4],
        [5.6, 2.9, 3.6, 1.3],
        [6.7, 3.1, 4.4, 1.4],
        [5.6, 3. , 4.5, 1.5],
        [5.8, 2.7, 4.1, 1. ],
        [6.2, 2.2, 4.5, 1.5],
        [5.6, 2.5, 3.9, 1.1],
        [5.9, 3.2, 4.8, 1.8],
        [6.1, 2.8, 4. , 1.3],
        [6.3, 2.5, 4.9, 1.5],
        [6.1, 2.8, 4.7, 1.2],
        [6.4, 2.9, 4.3, 1.3],
        [6.6, 3. , 4.4, 1.4],
        [6.8, 2.8, 4.8, 1.4],
        [6.7, 3. , 5. , 1.7],
        [6. , 2.9, 4.5, 1.5],
        [5.7, 2.6, 3.5, 1. ],
        [5.5, 2.4, 3.8, 1.1],
        [5.5, 2.4, 3.7, 1. ],
        [5.8, 2.7, 3.9, 1.2],
        [6. , 2.7, 5.1, 1.6],
        [5.4, 3. , 4.5, 1.5],
        [6. , 3.4, 4.5, 1.6],
        [6.7, 3.1, 4.7, 1.5],
        [6.3, 2.3, 4.4, 1.3],
        [5.6, 3. , 4.1, 1.3],
        [5.5, 2.5, 4. , 1.3],
        [5.5, 2.6, 4.4, 1.2],
        [6.1, 3. , 4.6, 1.4],
        [5.8, 2.6, 4. , 1.2],
        [5. , 2.3, 3.3, 1. ],
        [5.6, 2.7, 4.2, 1.3],
        [5.7, 3. , 4.2, 1.2],
        [5.7, 2.9, 4.2, 1.3],
        [6.2, 2.9, 4.3, 1.3],
        [5.1, 2.5, 3. , 1.1],
        [5.7, 2.8, 4.1, 1.3],
        [6.3, 3.3, 6. , 2.5],
        [5.8, 2.7, 5.1, 1.9],
        [7.1, 3. , 5.9, 2.1],
        [6.3, 2.9, 5.6, 1.8],
        [6.5, 3. , 5.8, 2.2],
        [7.6, 3. , 6.6, 2.1],
        [4.9, 2.5, 4.5, 1.7],
        [7.3, 2.9, 6.3, 1.8],
        [6.7, 2.5, 5.8, 1.8],
        [7.2, 3.6, 6.1, 2.5],
        [6.5, 3.2, 5.1, 2. ],
        [6.4, 2.7, 5.3, 1.9],
        [6.8, 3. , 5.5, 2.1],
        [5.7, 2.5, 5. , 2. ],
        [5.8, 2.8, 5.1, 2.4],
        [6.4, 3.2, 5.3, 2.3],
        [6.5, 3. , 5.5, 1.8],
        [7.7, 3.8, 6.7, 2.2],
        [7.7, 2.6, 6.9, 2.3],
        [6. , 2.2, 5. , 1.5],
        [6.9, 3.2, 5.7, 2.3],
        [5.6, 2.8, 4.9, 2. ],
        [7.7, 2.8, 6.7, 2. ],
        [6.3, 2.7, 4.9, 1.8],
        [6.7, 3.3, 5.7, 2.1],
        [7.2, 3.2, 6. , 1.8],
        [6.2, 2.8, 4.8, 1.8],
        [6.1, 3. , 4.9, 1.8],
        [6.4, 2.8, 5.6, 2.1],
        [7.2, 3. , 5.8, 1.6],
        [7.4, 2.8, 6.1, 1.9],
        [7.9, 3.8, 6.4, 2. ],
        [6.4, 2.8, 5.6, 2.2],
        [6.3, 2.8, 5.1, 1.5],
        [6.1, 2.6, 5.6, 1.4],
        [7.7, 3. , 6.1, 2.3],
        [6.3, 3.4, 5.6, 2.4],
        [6.4, 3.1, 5.5, 1.8],
        [6. , 3. , 4.8, 1.8],
        [6.9, 3.1, 5.4, 2.1],
        [6.7, 3.1, 5.6, 2.4],
        [6.9, 3.1, 5.1, 2.3],
        [5.8, 2.7, 5.1, 1.9],
        [6.8, 3.2, 5.9, 2.3],
        [6.7, 3.3, 5.7, 2.5],
        [6.7, 3. , 5.2, 2.3],
        [6.3, 2.5, 5. , 1.9],
        [6.5, 3. , 5.2, 2. ],
        [6.2, 3.4, 5.4, 2.3],
        [5.9, 3. , 5.1, 1.8]]),
 'target': array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
        2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
        2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]),
 'frame': None,
 'target_names': array(['setosa', 'versicolor', 'virginica'], dtype='

 
  data_x=data["data"]
data_y=data["target"]
 
  data_x.shape,data_y.shape
 
  ((150, 4), (150,))
 
  data_y=data_y.reshape([len(data_y),1])
data_y
 
  array([[0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2]])
 
  #法1 ，用拼接的方法
data=np.hstack([data_x,data_y])
 
  #法二： 用插入的方法
np.insert(data_x,data_x.shape[1],data_y,axis=1)
 
  array([[5.1, 3.5, 1.4, ..., 2. , 2. , 2. ],
       [4.9, 3. , 1.4, ..., 2. , 2. , 2. ],
       [4.7, 3.2, 1.3, ..., 2. , 2. , 2. ],
       ...,
       [6.5, 3. , 5.2, ..., 2. , 2. , 2. ],
       [6.2, 3.4, 5.4, ..., 2. , 2. , 2. ],
       [5.9, 3. , 5.1, ..., 2. , 2. , 2. ]])
 
  data=pd.DataFrame(data,columns=["F1","F2","F3","F4","target"])
data
 
   
   
   
    
     
      
     F1 
     F2 
     F3 
     F4 
     target 
     
    
    
     
     0 
     5.1 
     3.5 
     1.4 
     0.2 
     0.0 
     
     
     1 
     4.9 
     3.0 
     1.4 
     0.2 
     0.0 
     
     
     2 
     4.7 
     3.2 
     1.3 
     0.2 
     0.0 
     
     
     3 
     4.6 
     3.1 
     1.5 
     0.2 
     0.0 
     
     
     4 
     5.0 
     3.6 
     1.4 
     0.2 
     0.0 
     
     
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     
     
     145 
     6.7 
     3.0 
     5.2 
     2.3 
     2.0 
     
     
     146 
     6.3 
     2.5 
     5.0 
     1.9 
     2.0 
     
     
     147 
     6.5 
     3.0 
     5.2 
     2.0 
     2.0 
     
     
     148 
     6.2 
     3.4 
     5.4 
     2.3 
     2.0 
     
     
     149 
     5.9 
     3.0 
     5.1 
     1.8 
     2.0 
     
    
   
  150 rows × 5 columns 
  data.insert(0,"ones",1)
 
  data
 
   
   
   
    
     
      
     ones 
     F1 
     F2 
     F3 
     F4 
     target 
     
    
    
     
     0 
     1 
     5.1 
     3.5 
     1.4 
     0.2 
     0.0 
     
     
     1 
     1 
     4.9 
     3.0 
     1.4 
     0.2 
     0.0 
     
     
     2 
     1 
     4.7 
     3.2 
     1.3 
     0.2 
     0.0 
     
     
     3 
     1 
     4.6 
     3.1 
     1.5 
     0.2 
     0.0 
     
     
     4 
     1 
     5.0 
     3.6 
     1.4 
     0.2 
     0.0 
     
     
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     
     
     145 
     1 
     6.7 
     3.0 
     5.2 
     2.3 
     2.0 
     
     
     146 
     1 
     6.3 
     2.5 
     5.0 
     1.9 
     2.0 
     
     
     147 
     1 
     6.5 
     3.0 
     5.2 
     2.0 
     2.0 
     
     
     148 
     1 
     6.2 
     3.4 
     5.4 
     2.3 
     2.0 
     
     
     149 
     1 
     5.9 
     3.0 
     5.1 
     1.8 
     2.0 
     
    
   
  150 rows × 6 columns 
  data["target"]=data["target"].astype("int32")
 
  data
 
   
   
   
    
     
      
     ones 
     F1 
     F2 
     F3 
     F4 
     target 
     
    
    
     
     0 
     1 
     5.1 
     3.5 
     1.4 
     0.2 
     0 
     
     
     1 
     1 
     4.9 
     3.0 
     1.4 
     0.2 
     0 
     
     
     2 
     1 
     4.7 
     3.2 
     1.3 
     0.2 
     0 
     
     
     3 
     1 
     4.6 
     3.1 
     1.5 
     0.2 
     0 
     
     
     4 
     1 
     5.0 
     3.6 
     1.4 
     0.2 
     0 
     
     
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     
     
     145 
     1 
     6.7 
     3.0 
     5.2 
     2.3 
     2 
     
     
     146 
     1 
     6.3 
     2.5 
     5.0 
     1.9 
     2 
     
     
     147 
     1 
     6.5 
     3.0 
     5.2 
     2.0 
     2 
     
     
     148 
     1 
     6.2 
     3.4 
     5.4 
     2.3 
     2 
     
     
     149 
     1 
     5.9 
     3.0 
     5.1 
     1.8 
     2 
     
    
   
  150 rows × 6 columns 
  1.2 训练数据的准备 
  data_x
 
  array([[5.1, 3.5, 1.4, 0.2],
       [4.9, 3. , 1.4, 0.2],
       [4.7, 3.2, 1.3, 0.2],
       [4.6, 3.1, 1.5, 0.2],
       [5. , 3.6, 1.4, 0.2],
       [5.4, 3.9, 1.7, 0.4],
       [4.6, 3.4, 1.4, 0.3],
       [5. , 3.4, 1.5, 0.2],
       [4.4, 2.9, 1.4, 0.2],
       [4.9, 3.1, 1.5, 0.1],
       [5.4, 3.7, 1.5, 0.2],
       [4.8, 3.4, 1.6, 0.2],
       [4.8, 3. , 1.4, 0.1],
       [4.3, 3. , 1.1, 0.1],
       [5.8, 4. , 1.2, 0.2],
       [5.7, 4.4, 1.5, 0.4],
       [5.4, 3.9, 1.3, 0.4],
       [5.1, 3.5, 1.4, 0.3],
       [5.7, 3.8, 1.7, 0.3],
       [5.1, 3.8, 1.5, 0.3],
       [5.4, 3.4, 1.7, 0.2],
       [5.1, 3.7, 1.5, 0.4],
       [4.6, 3.6, 1. , 0.2],
       [5.1, 3.3, 1.7, 0.5],
       [4.8, 3.4, 1.9, 0.2],
       [5. , 3. , 1.6, 0.2],
       [5. , 3.4, 1.6, 0.4],
       [5.2, 3.5, 1.5, 0.2],
       [5.2, 3.4, 1.4, 0.2],
       [4.7, 3.2, 1.6, 0.2],
       [4.8, 3.1, 1.6, 0.2],
       [5.4, 3.4, 1.5, 0.4],
       [5.2, 4.1, 1.5, 0.1],
       [5.5, 4.2, 1.4, 0.2],
       [4.9, 3.1, 1.5, 0.2],
       [5. , 3.2, 1.2, 0.2],
       [5.5, 3.5, 1.3, 0.2],
       [4.9, 3.6, 1.4, 0.1],
       [4.4, 3. , 1.3, 0.2],
       [5.1, 3.4, 1.5, 0.2],
       [5. , 3.5, 1.3, 0.3],
       [4.5, 2.3, 1.3, 0.3],
       [4.4, 3.2, 1.3, 0.2],
       [5. , 3.5, 1.6, 0.6],
       [5.1, 3.8, 1.9, 0.4],
       [4.8, 3. , 1.4, 0.3],
       [5.1, 3.8, 1.6, 0.2],
       [4.6, 3.2, 1.4, 0.2],
       [5.3, 3.7, 1.5, 0.2],
       [5. , 3.3, 1.4, 0.2],
       [7. , 3.2, 4.7, 1.4],
       [6.4, 3.2, 4.5, 1.5],
       [6.9, 3.1, 4.9, 1.5],
       [5.5, 2.3, 4. , 1.3],
       [6.5, 2.8, 4.6, 1.5],
       [5.7, 2.8, 4.5, 1.3],
       [6.3, 3.3, 4.7, 1.6],
       [4.9, 2.4, 3.3, 1. ],
       [6.6, 2.9, 4.6, 1.3],
       [5.2, 2.7, 3.9, 1.4],
       [5. , 2. , 3.5, 1. ],
       [5.9, 3. , 4.2, 1.5],
       [6. , 2.2, 4. , 1. ],
       [6.1, 2.9, 4.7, 1.4],
       [5.6, 2.9, 3.6, 1.3],
       [6.7, 3.1, 4.4, 1.4],
       [5.6, 3. , 4.5, 1.5],
       [5.8, 2.7, 4.1, 1. ],
       [6.2, 2.2, 4.5, 1.5],
       [5.6, 2.5, 3.9, 1.1],
       [5.9, 3.2, 4.8, 1.8],
       [6.1, 2.8, 4. , 1.3],
       [6.3, 2.5, 4.9, 1.5],
       [6.1, 2.8, 4.7, 1.2],
       [6.4, 2.9, 4.3, 1.3],
       [6.6, 3. , 4.4, 1.4],
       [6.8, 2.8, 4.8, 1.4],
       [6.7, 3. , 5. , 1.7],
       [6. , 2.9, 4.5, 1.5],
       [5.7, 2.6, 3.5, 1. ],
       [5.5, 2.4, 3.8, 1.1],
       [5.5, 2.4, 3.7, 1. ],
       [5.8, 2.7, 3.9, 1.2],
       [6. , 2.7, 5.1, 1.6],
       [5.4, 3. , 4.5, 1.5],
       [6. , 3.4, 4.5, 1.6],
       [6.7, 3.1, 4.7, 1.5],
       [6.3, 2.3, 4.4, 1.3],
       [5.6, 3. , 4.1, 1.3],
       [5.5, 2.5, 4. , 1.3],
       [5.5, 2.6, 4.4, 1.2],
       [6.1, 3. , 4.6, 1.4],
       [5.8, 2.6, 4. , 1.2],
       [5. , 2.3, 3.3, 1. ],
       [5.6, 2.7, 4.2, 1.3],
       [5.7, 3. , 4.2, 1.2],
       [5.7, 2.9, 4.2, 1.3],
       [6.2, 2.9, 4.3, 1.3],
       [5.1, 2.5, 3. , 1.1],
       [5.7, 2.8, 4.1, 1.3],
       [6.3, 3.3, 6. , 2.5],
       [5.8, 2.7, 5.1, 1.9],
       [7.1, 3. , 5.9, 2.1],
       [6.3, 2.9, 5.6, 1.8],
       [6.5, 3. , 5.8, 2.2],
       [7.6, 3. , 6.6, 2.1],
       [4.9, 2.5, 4.5, 1.7],
       [7.3, 2.9, 6.3, 1.8],
       [6.7, 2.5, 5.8, 1.8],
       [7.2, 3.6, 6.1, 2.5],
       [6.5, 3.2, 5.1, 2. ],
       [6.4, 2.7, 5.3, 1.9],
       [6.8, 3. , 5.5, 2.1],
       [5.7, 2.5, 5. , 2. ],
       [5.8, 2.8, 5.1, 2.4],
       [6.4, 3.2, 5.3, 2.3],
       [6.5, 3. , 5.5, 1.8],
       [7.7, 3.8, 6.7, 2.2],
       [7.7, 2.6, 6.9, 2.3],
       [6. , 2.2, 5. , 1.5],
       [6.9, 3.2, 5.7, 2.3],
       [5.6, 2.8, 4.9, 2. ],
       [7.7, 2.8, 6.7, 2. ],
       [6.3, 2.7, 4.9, 1.8],
       [6.7, 3.3, 5.7, 2.1],
       [7.2, 3.2, 6. , 1.8],
       [6.2, 2.8, 4.8, 1.8],
       [6.1, 3. , 4.9, 1.8],
       [6.4, 2.8, 5.6, 2.1],
       [7.2, 3. , 5.8, 1.6],
       [7.4, 2.8, 6.1, 1.9],
       [7.9, 3.8, 6.4, 2. ],
       [6.4, 2.8, 5.6, 2.2],
       [6.3, 2.8, 5.1, 1.5],
       [6.1, 2.6, 5.6, 1.4],
       [7.7, 3. , 6.1, 2.3],
       [6.3, 3.4, 5.6, 2.4],
       [6.4, 3.1, 5.5, 1.8],
       [6. , 3. , 4.8, 1.8],
       [6.9, 3.1, 5.4, 2.1],
       [6.7, 3.1, 5.6, 2.4],
       [6.9, 3.1, 5.1, 2.3],
       [5.8, 2.7, 5.1, 1.9],
       [6.8, 3.2, 5.9, 2.3],
       [6.7, 3.3, 5.7, 2.5],
       [6.7, 3. , 5.2, 2.3],
       [6.3, 2.5, 5. , 1.9],
       [6.5, 3. , 5.2, 2. ],
       [6.2, 3.4, 5.4, 2.3],
       [5.9, 3. , 5.1, 1.8]])
 
  data_x=np.insert(data_x,0,1,axis=1)
 
  data_x.shape,data_y.shape
 
  ((150, 5), (150, 1))
 
  #训练数据的特征和标签
data_x,data_y
 
  (array([[1. , 5.1, 3.5, 1.4, 0.2],
        [1. , 4.9, 3. , 1.4, 0.2],
        [1. , 4.7, 3.2, 1.3, 0.2],
        [1. , 4.6, 3.1, 1.5, 0.2],
        [1. , 5. , 3.6, 1.4, 0.2],
        [1. , 5.4, 3.9, 1.7, 0.4],
        [1. , 4.6, 3.4, 1.4, 0.3],
        [1. , 5. , 3.4, 1.5, 0.2],
        [1. , 4.4, 2.9, 1.4, 0.2],
        [1. , 4.9, 3.1, 1.5, 0.1],
        [1. , 5.4, 3.7, 1.5, 0.2],
        [1. , 4.8, 3.4, 1.6, 0.2],
        [1. , 4.8, 3. , 1.4, 0.1],
        [1. , 4.3, 3. , 1.1, 0.1],
        [1. , 5.8, 4. , 1.2, 0.2],
        [1. , 5.7, 4.4, 1.5, 0.4],
        [1. , 5.4, 3.9, 1.3, 0.4],
        [1. , 5.1, 3.5, 1.4, 0.3],
        [1. , 5.7, 3.8, 1.7, 0.3],
        [1. , 5.1, 3.8, 1.5, 0.3],
        [1. , 5.4, 3.4, 1.7, 0.2],
        [1. , 5.1, 3.7, 1.5, 0.4],
        [1. , 4.6, 3.6, 1. , 0.2],
        [1. , 5.1, 3.3, 1.7, 0.5],
        [1. , 4.8, 3.4, 1.9, 0.2],
        [1. , 5. , 3. , 1.6, 0.2],
        [1. , 5. , 3.4, 1.6, 0.4],
        [1. , 5.2, 3.5, 1.5, 0.2],
        [1. , 5.2, 3.4, 1.4, 0.2],
        [1. , 4.7, 3.2, 1.6, 0.2],
        [1. , 4.8, 3.1, 1.6, 0.2],
        [1. , 5.4, 3.4, 1.5, 0.4],
        [1. , 5.2, 4.1, 1.5, 0.1],
        [1. , 5.5, 4.2, 1.4, 0.2],
        [1. , 4.9, 3.1, 1.5, 0.2],
        [1. , 5. , 3.2, 1.2, 0.2],
        [1. , 5.5, 3.5, 1.3, 0.2],
        [1. , 4.9, 3.6, 1.4, 0.1],
        [1. , 4.4, 3. , 1.3, 0.2],
        [1. , 5.1, 3.4, 1.5, 0.2],
        [1. , 5. , 3.5, 1.3, 0.3],
        [1. , 4.5, 2.3, 1.3, 0.3],
        [1. , 4.4, 3.2, 1.3, 0.2],
        [1. , 5. , 3.5, 1.6, 0.6],
        [1. , 5.1, 3.8, 1.9, 0.4],
        [1. , 4.8, 3. , 1.4, 0.3],
        [1. , 5.1, 3.8, 1.6, 0.2],
        [1. , 4.6, 3.2, 1.4, 0.2],
        [1. , 5.3, 3.7, 1.5, 0.2],
        [1. , 5. , 3.3, 1.4, 0.2],
        [1. , 7. , 3.2, 4.7, 1.4],
        [1. , 6.4, 3.2, 4.5, 1.5],
        [1. , 6.9, 3.1, 4.9, 1.5],
        [1. , 5.5, 2.3, 4. , 1.3],
        [1. , 6.5, 2.8, 4.6, 1.5],
        [1. , 5.7, 2.8, 4.5, 1.3],
        [1. , 6.3, 3.3, 4.7, 1.6],
        [1. , 4.9, 2.4, 3.3, 1. ],
        [1. , 6.6, 2.9, 4.6, 1.3],
        [1. , 5.2, 2.7, 3.9, 1.4],
        [1. , 5. , 2. , 3.5, 1. ],
        [1. , 5.9, 3. , 4.2, 1.5],
        [1. , 6. , 2.2, 4. , 1. ],
        [1. , 6.1, 2.9, 4.7, 1.4],
        [1. , 5.6, 2.9, 3.6, 1.3],
        [1. , 6.7, 3.1, 4.4, 1.4],
        [1. , 5.6, 3. , 4.5, 1.5],
        [1. , 5.8, 2.7, 4.1, 1. ],
        [1. , 6.2, 2.2, 4.5, 1.5],
        [1. , 5.6, 2.5, 3.9, 1.1],
        [1. , 5.9, 3.2, 4.8, 1.8],
        [1. , 6.1, 2.8, 4. , 1.3],
        [1. , 6.3, 2.5, 4.9, 1.5],
        [1. , 6.1, 2.8, 4.7, 1.2],
        [1. , 6.4, 2.9, 4.3, 1.3],
        [1. , 6.6, 3. , 4.4, 1.4],
        [1. , 6.8, 2.8, 4.8, 1.4],
        [1. , 6.7, 3. , 5. , 1.7],
        [1. , 6. , 2.9, 4.5, 1.5],
        [1. , 5.7, 2.6, 3.5, 1. ],
        [1. , 5.5, 2.4, 3.8, 1.1],
        [1. , 5.5, 2.4, 3.7, 1. ],
        [1. , 5.8, 2.7, 3.9, 1.2],
        [1. , 6. , 2.7, 5.1, 1.6],
        [1. , 5.4, 3. , 4.5, 1.5],
        [1. , 6. , 3.4, 4.5, 1.6],
        [1. , 6.7, 3.1, 4.7, 1.5],
        [1. , 6.3, 2.3, 4.4, 1.3],
        [1. , 5.6, 3. , 4.1, 1.3],
        [1. , 5.5, 2.5, 4. , 1.3],
        [1. , 5.5, 2.6, 4.4, 1.2],
        [1. , 6.1, 3. , 4.6, 1.4],
        [1. , 5.8, 2.6, 4. , 1.2],
        [1. , 5. , 2.3, 3.3, 1. ],
        [1. , 5.6, 2.7, 4.2, 1.3],
        [1. , 5.7, 3. , 4.2, 1.2],
        [1. , 5.7, 2.9, 4.2, 1.3],
        [1. , 6.2, 2.9, 4.3, 1.3],
        [1. , 5.1, 2.5, 3. , 1.1],
        [1. , 5.7, 2.8, 4.1, 1.3],
        [1. , 6.3, 3.3, 6. , 2.5],
        [1. , 5.8, 2.7, 5.1, 1.9],
        [1. , 7.1, 3. , 5.9, 2.1],
        [1. , 6.3, 2.9, 5.6, 1.8],
        [1. , 6.5, 3. , 5.8, 2.2],
        [1. , 7.6, 3. , 6.6, 2.1],
        [1. , 4.9, 2.5, 4.5, 1.7],
        [1. , 7.3, 2.9, 6.3, 1.8],
        [1. , 6.7, 2.5, 5.8, 1.8],
        [1. , 7.2, 3.6, 6.1, 2.5],
        [1. , 6.5, 3.2, 5.1, 2. ],
        [1. , 6.4, 2.7, 5.3, 1.9],
        [1. , 6.8, 3. , 5.5, 2.1],
        [1. , 5.7, 2.5, 5. , 2. ],
        [1. , 5.8, 2.8, 5.1, 2.4],
        [1. , 6.4, 3.2, 5.3, 2.3],
        [1. , 6.5, 3. , 5.5, 1.8],
        [1. , 7.7, 3.8, 6.7, 2.2],
        [1. , 7.7, 2.6, 6.9, 2.3],
        [1. , 6. , 2.2, 5. , 1.5],
        [1. , 6.9, 3.2, 5.7, 2.3],
        [1. , 5.6, 2.8, 4.9, 2. ],
        [1. , 7.7, 2.8, 6.7, 2. ],
        [1. , 6.3, 2.7, 4.9, 1.8],
        [1. , 6.7, 3.3, 5.7, 2.1],
        [1. , 7.2, 3.2, 6. , 1.8],
        [1. , 6.2, 2.8, 4.8, 1.8],
        [1. , 6.1, 3. , 4.9, 1.8],
        [1. , 6.4, 2.8, 5.6, 2.1],
        [1. , 7.2, 3. , 5.8, 1.6],
        [1. , 7.4, 2.8, 6.1, 1.9],
        [1. , 7.9, 3.8, 6.4, 2. ],
        [1. , 6.4, 2.8, 5.6, 2.2],
        [1. , 6.3, 2.8, 5.1, 1.5],
        [1. , 6.1, 2.6, 5.6, 1.4],
        [1. , 7.7, 3. , 6.1, 2.3],
        [1. , 6.3, 3.4, 5.6, 2.4],
        [1. , 6.4, 3.1, 5.5, 1.8],
        [1. , 6. , 3. , 4.8, 1.8],
        [1. , 6.9, 3.1, 5.4, 2.1],
        [1. , 6.7, 3.1, 5.6, 2.4],
        [1. , 6.9, 3.1, 5.1, 2.3],
        [1. , 5.8, 2.7, 5.1, 1.9],
        [1. , 6.8, 3.2, 5.9, 2.3],
        [1. , 6.7, 3.3, 5.7, 2.5],
        [1. , 6.7, 3. , 5.2, 2.3],
        [1. , 6.3, 2.5, 5. , 1.9],
        [1. , 6.5, 3. , 5.2, 2. ],
        [1. , 6.2, 3.4, 5.4, 2.3],
        [1. , 5.9, 3. , 5.1, 1.8]]),
 array([[0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [0],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [1],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2],
        [2]]))
 
  由于有三个类别，那么在训练时三类数据要分开 
  data1=data.copy()
 
  data1
 
   
   
   
    
     
      
     ones 
     F1 
     F2 
     F3 
     F4 
     target 
     
    
    
     
     0 
     1 
     5.1 
     3.5 
     1.4 
     0.2 
     0 
     
     
     1 
     1 
     4.9 
     3.0 
     1.4 
     0.2 
     0 
     
     
     2 
     1 
     4.7 
     3.2 
     1.3 
     0.2 
     0 
     
     
     3 
     1 
     4.6 
     3.1 
     1.5 
     0.2 
     0 
     
     
     4 
     1 
     5.0 
     3.6 
     1.4 
     0.2 
     0 
     
     
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     
     
     145 
     1 
     6.7 
     3.0 
     5.2 
     2.3 
     2 
     
     
     146 
     1 
     6.3 
     2.5 
     5.0 
     1.9 
     2 
     
     
     147 
     1 
     6.5 
     3.0 
     5.2 
     2.0 
     2 
     
     
     148 
     1 
     6.2 
     3.4 
     5.4 
     2.3 
     2 
     
     
     149 
     1 
     5.9 
     3.0 
     5.1 
     1.8 
     2 
     
    
   
  150 rows × 6 columns 
  data 
  data1.loc[data["target"]!=0,"target"]=0
data1.loc[data["target"]==0,"target"]=1
 
  data1
 
   
   
   
    
     
      
     ones 
     F1 
     F2 
     F3 
     F4 
     target 
     
    
    
     
     0 
     1 
     5.1 
     3.5 
     1.4 
     0.2 
     1 
     
     
     1 
     1 
     4.9 
     3.0 
     1.4 
     0.2 
     1 
     
     
     2 
     1 
     4.7 
     3.2 
     1.3 
     0.2 
     1 
     
     
     3 
     1 
     4.6 
     3.1 
     1.5 
     0.2 
     1 
     
     
     4 
     1 
     5.0 
     3.6 
     1.4 
     0.2 
     1 
     
     
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     
     
     145 
     1 
     6.7 
     3.0 
     5.2 
     2.3 
     0 
     
     
     146 
     1 
     6.3 
     2.5 
     5.0 
     1.9 
     0 
     
     
     147 
     1 
     6.5 
     3.0 
     5.2 
     2.0 
     0 
     
     
     148 
     1 
     6.2 
     3.4 
     5.4 
     2.3 
     0 
     
     
     149 
     1 
     5.9 
     3.0 
     5.1 
     1.8 
     0 
     
    
   
  150 rows × 6 columns 
  data1_x=data1.iloc[:,:data1.shape[1]-1].values
data1_y=data1.iloc[:,data1.shape[1]-1].values
data1_x.shape,data1_y.shape
 
  ((150, 5), (150,))
 
  #针对第二类，即第二个分类器的数据
data2=data.copy()
data2.loc[data["target"]==1,"target"]=1
data2.loc[data["target"]!=1,"target"]=0
data2["target"]==0
 
  0      True
1      True
2      True
3      True
4      True
       ... 
145    True
146    True
147    True
148    True
149    True
Name: target, Length: 150, dtype: bool
 
  data2.shape[1]
 
  6
 
  data2.iloc[50:55,:]
 
   
   
   
    
     
      
     ones 
     F1 
     F2 
     F3 
     F4 
     target 
     
    
    
     
     50 
     1 
     7.0 
     3.2 
     4.7 
     1.4 
     1 
     
     
     51 
     1 
     6.4 
     3.2 
     4.5 
     1.5 
     1 
     
     
     52 
     1 
     6.9 
     3.1 
     4.9 
     1.5 
     1 
     
     
     53 
     1 
     5.5 
     2.3 
     4.0 
     1.3 
     1 
     
     
     54 
     1 
     6.5 
     2.8 
     4.6 
     1.5 
     1 
     
    
   
  data2_x=data2.iloc[:,:data2.shape[1]-1].values
data2_y=data2.iloc[:,data2.shape[1]-1].values
 
  #针对第三类，即第三个分类器的数据
data3=data.copy()
data3.loc[data["target"]==2,"target"]=1
data3.loc[data["target"]!=2,"target"]=0
data3
 
   
   
   
    
     
      
     ones 
     F1 
     F2 
     F3 
     F4 
     target 
     
    
    
     
     0 
     1 
     5.1 
     3.5 
     1.4 
     0.2 
     0 
     
     
     1 
     1 
     4.9 
     3.0 
     1.4 
     0.2 
     0 
     
     
     2 
     1 
     4.7 
     3.2 
     1.3 
     0.2 
     0 
     
     
     3 
     1 
     4.6 
     3.1 
     1.5 
     0.2 
     0 
     
     
     4 
     1 
     5.0 
     3.6 
     1.4 
     0.2 
     0 
     
     
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     
     
     145 
     1 
     6.7 
     3.0 
     5.2 
     2.3 
     1 
     
     
     146 
     1 
     6.3 
     2.5 
     5.0 
     1.9 
     1 
     
     
     147 
     1 
     6.5 
     3.0 
     5.2 
     2.0 
     1 
     
     
     148 
     1 
     6.2 
     3.4 
     5.4 
     2.3 
     1 
     
     
     149 
     1 
     5.9 
     3.0 
     5.1 
     1.8 
     1 
     
    
   
  150 rows × 6 columns 
  data3_x=data3.iloc[:,:data3.shape[1]-1].values
data3_y=data3.iloc[:,data3.shape[1]-1].values
 
  1.3 定义假设函数，代价函数，梯度下降算法（从实验3复制过来） 
  def sigmoid(z):
    return 1 / (1 + np.exp(-z))
 
  def h(X,w):
    z=X@w
    h=sigmoid(z)
    return h
 
  #代价函数构造
def cost(X,w,y):
    #当X(m,n+1),y(m,),w(n+1,1)
    y_hat=sigmoid(X@w)
    right=np.multiply(y.ravel(),np.log(y_hat).ravel())+np.multiply((1-y).ravel(),np.log(1-y_hat).ravel())
    cost=-np.sum(right)/X.shape[0]
    return cost
 
  def sigmoid(z):
    return 1 / (1 + np.exp(-z))

def h(X,w):
    z=X@w
    h=sigmoid(z)
    return h

#代价函数构造
def cost(X,w,y):
    #当X(m,n+1),y(m,),w(n+1,1)
    y_hat=sigmoid(X@w)
    right=np.multiply(y.ravel(),np.log(y_hat).ravel())+np.multiply((1-y).ravel(),np.log(1-y_hat).ravel())
    cost=-np.sum(right)/X.shape[0]
    return cost



def grandient(X,y,iter_num,alpha):
    y=y.reshape((X.shape[0],1))
    w=np.zeros((X.shape[1],1))
    cost_lst=[]  
    for i in range(iter_num):
        y_pred=h(X,w)-y
        temp=np.zeros((X.shape[1],1))
        for j in range(X.shape[1]):
            right=np.multiply(y_pred.ravel(),X[:,j])
            
            gradient=1/(X.shape[0])*(np.sum(right))
            temp[j,0]=w[j,0]-alpha*gradient
        w=temp
        cost_lst.append(cost(X,w,y.ravel()))
    return w,cost_lst
 
  1.4 调用梯度下降算法来学习三个分类模型的参数 
  #初始化超参数
iter_num,alpha=600000,0.001
 
  #训练第一个模型
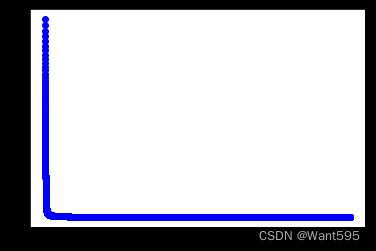
w1,cost_lst1=grandient(data1_x,data1_y,iter_num,alpha)
 
  import matplotlib.pyplot as plt
plt.plot(range(iter_num),cost_lst1,"b-o")
 
  []
 
   
  #训练第二个模型
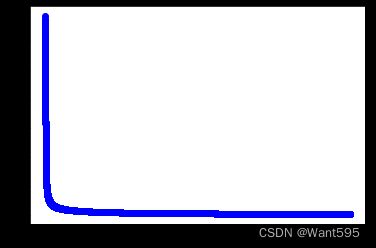
w2,cost_lst2=grandient(data2_x,data2_y,iter_num,alpha)
 
  import matplotlib.pyplot as plt
plt.plot(range(iter_num),cost_lst2,"b-o")
 
  []
 
   
  #训练第三个模型
w3,cost_lst3=grandient(data3_x,data3_y,iter_num,alpha)
 
  w3
 
  array([[-3.22437049],
       [-3.50214058],
       [-3.50286355],
       [ 5.16580317],
       [ 5.89898368]])
 
  import matplotlib.pyplot as plt
plt.plot(range(iter_num),cost_lst3,"b-o")
 
  []
 
   
  1.5 利用模型进行预测 
  h(data_x,w3)
 
  array([[1.48445441e-11],
       [1.72343968e-10],
       [1.02798153e-10],
       [5.81975546e-10],
       [1.48434710e-11],
       [1.95971176e-11],
       [2.18959639e-10],
       [5.01346874e-11],
       [1.40930075e-09],
       [1.12830635e-10],
       [4.31888744e-12],
       [1.69308343e-10],
       [1.35613372e-10],
       [1.65858883e-10],
       [7.89880725e-14],
       [4.23224675e-13],
       [2.48199140e-12],
       [2.67766642e-11],
       [5.39314286e-12],
       [1.56935848e-11],
       [3.47096426e-11],
       [4.01827075e-11],
       [7.63005509e-12],
       [8.26864773e-10],
       [7.97484594e-10],
       [3.41189783e-10],
       [2.73442178e-10],
       [1.75314894e-11],
       [1.48456174e-11],
       [4.84204982e-10],
       [4.84239990e-10],
       [4.01914238e-11],
       [1.18813180e-12],
       [3.14985611e-13],
       [2.03524473e-10],
       [2.14461446e-11],
       [2.18189955e-12],
       [1.16799745e-11],
       [5.92281641e-10],
       [3.53217554e-11],
       [2.26727669e-11],
       [8.74004884e-09],
       [2.93949962e-10],
       [6.26783110e-10],
       [2.23513465e-10],
       [4.41246960e-10],
       [1.45841303e-11],
       [2.44584721e-10],
       [6.13010507e-12],
       [4.24539165e-11],
       [1.64123143e-03],
       [8.55503211e-03],
       [1.65105645e-02],
       [9.87814122e-02],
       [3.97290777e-02],
       [1.11076040e-01],
       [4.19003715e-02],
       [2.88426221e-03],
       [6.27161978e-03],
       [7.67020481e-02],
       [2.27204861e-02],
       [2.08212169e-02],
       [4.58067633e-03],
       [9.90450665e-02],
       [1.19419048e-03],
       [1.41462060e-03],
       [2.22638069e-01],
       [2.68940904e-03],
       [3.66014737e-01],
       [6.97791873e-03],
       [5.78803255e-01],
       [2.32071970e-03],
       [5.28941621e-01],
       [4.57649874e-02],
       [2.69208900e-03],
       [2.84603646e-03],
       [2.20421076e-02],
       [2.07507605e-01],
       [9.10460936e-02],
       [2.44824946e-04],
       [8.37509821e-03],
       [2.78543808e-03],
       [3.11283202e-03],
       [8.89831833e-01],
       [3.65880536e-01],
       [3.03993844e-02],
       [1.18930239e-02],
       [4.99150151e-02],
       [1.10252946e-02],
       [5.15923462e-02],
       [1.43653056e-01],
       [4.41610209e-02],
       [7.37513950e-03],
       [2.88447014e-03],
       [5.07366744e-02],
       [7.24617687e-03],
       [1.83460602e-02],
       [5.40874928e-03],
       [3.87210511e-04],
       [1.55791816e-02],
       [9.99862942e-01],
       [9.89637526e-01],
       [9.86183040e-01],
       [9.83705644e-01],
       [9.98410187e-01],
       [9.97834502e-01],
       [9.84208537e-01],
       [9.85434538e-01],
       [9.94141336e-01],
       [9.94561329e-01],
       [7.20333384e-01],
       [9.70431293e-01],
       [9.62754456e-01],
       [9.96609064e-01],
       [9.99222270e-01],
       [9.83684437e-01],
       [9.26437633e-01],
       [9.83486260e-01],
       [9.99950496e-01],
       [9.39002061e-01],
       [9.88043323e-01],
       [9.88637702e-01],
       [9.98357641e-01],
       [7.65848930e-01],
       [9.73006160e-01],
       [8.76969899e-01],
       [6.61137141e-01],
       [6.97324053e-01],
       [9.97185846e-01],
       [6.11033594e-01],
       [9.77494647e-01],
       [6.58573810e-01],
       [9.98437920e-01],
       [5.24529693e-01],
       [9.70465066e-01],
       [9.87624920e-01],
       [9.97236435e-01],
       [9.26432706e-01],
       [6.61104746e-01],
       [8.84442100e-01],
       [9.96082862e-01],
       [8.40940308e-01],
       [9.89637526e-01],
       [9.96974990e-01],
       [9.97386310e-01],
       [9.62040470e-01],
       [9.52214579e-01],
       [8.96902215e-01],
       [9.90200940e-01],
       [9.28785160e-01]])
 
  #将数据输入三个模型的看看结果
multi_pred=pd.DataFrame(zip(h(data_x,w1).ravel(),h(data_x,w2).ravel(),h(data_x,w3).ravel()))
multi_pred
 
   
   
   
    
     
      
     0 
     1 
     2 
     
    
    
     
     0 
     0.999297 
     0.108037 
     1.484454e-11 
     
     
     1 
     0.997061 
     0.270814 
     1.723440e-10 
     
     
     2 
     0.998633 
     0.164710 
     1.027982e-10 
     
     
     3 
     0.995774 
     0.231910 
     5.819755e-10 
     
     
     4 
     0.999415 
     0.085259 
     1.484347e-11 
     
     
     ... 
     ... 
     ... 
     ... 
     
     
     145 
     0.000007 
     0.127574 
     9.620405e-01 
     
     
     146 
     0.000006 
     0.496389 
     9.522146e-01 
     
     
     147 
     0.000010 
     0.234745 
     8.969022e-01 
     
     
     148 
     0.000006 
     0.058444 
     9.902009e-01 
     
     
     149 
     0.000014 
     0.284295 
     9.287852e-01 
     
    
   
  150 rows × 3 columns 
  multi_pred.values[:3]
 
  array([[9.99297209e-01, 1.08037473e-01, 1.48445441e-11],
       [9.97060801e-01, 2.70813780e-01, 1.72343968e-10],
       [9.98632728e-01, 1.64709623e-01, 1.02798153e-10]])
 
  #每个样本的预测值
np.argmax(multi_pred.values,axis=1)
 
  array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2,
       2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2], dtype=int64)
 
  #每个样本的真实值
data_y
 
  array([[0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [0],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [1],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2],
       [2]])
 
  1.6 评估模型 
  np.argmax(multi_pred.values,axis=1)==data_y.ravel()
 
  array([ True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True, False,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True, False, False,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True, False,  True,  True,  True, False,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True])
 
  np.sum(np.argmax(multi_pred.values,axis=1)==data_y.ravel())
 
  145
 
  np.sum(np.argmax(multi_pred.values,axis=1)==data_y.ravel())/len(data)
 
  0.9666666666666667
 
  1.7 试试sklearn 
  from sklearn.linear_model import LogisticRegression
#建立第一个模型
clf1=LogisticRegression()
clf1.fit(data1_x,data1_y)
#建立第二个模型
clf2=LogisticRegression()
clf2.fit(data2_x,data2_y)
#建立第三个模型
clf3=LogisticRegression()
clf3.fit(data3_x,data3_y)
 
  LogisticRegression()
 
  y_pred1=clf1.predict(data_x)
y_pred2=clf2.predict(data_x)
y_pred3=clf3.predict(data_x)
 
  #可视化各模型的预测结果
multi_pred=pd.DataFrame(zip(y_pred1,y_pred2,y_pred3),columns=["模型1","模糊2","模型3"])
multi_pred
 
   
   
   
    
     
      
     模型1 
     模糊2 
     模型3 
     
    
    
     
     0 
     1 
     0 
     0 
     
     
     1 
     1 
     0 
     0 
     
     
     2 
     1 
     0 
     0 
     
     
     3 
     1 
     0 
     0 
     
     
     4 
     1 
     0 
     0 
     
     
     ... 
     ... 
     ... 
     ... 
     
     
     145 
     0 
     0 
     1 
     
     
     146 
     0 
     1 
     1 
     
     
     147 
     0 
     0 
     1 
     
     
     148 
     0 
     0 
     1 
     
     
     149 
     0 
     0 
     1 
     
    
   
  150 rows × 3 columns 
  #判断预测结果
np.argmax(multi_pred.values,axis=1)
 
  array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0,
       0, 1, 1, 1, 2, 0, 1, 1, 0, 0, 0, 2, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1,
       0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 2, 2, 2, 2, 2, 2, 1, 1, 1, 2,
       2, 2, 2, 1, 2, 2, 2, 2, 1, 1, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 1, 2,
       2, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2], dtype=int64)
 
  data_y.ravel()
 
  array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])
 
  #计算准确率
np.sum(np.argmax(multi_pred.values,axis=1)==data_y.ravel())/data.shape[0]
 
  0.7333333333333333
 
  实验4(1) 请动手完成你们第一个多分类问题，祝好运！完成下面代码 
  2.1 数据读取 
  data_x,data_y=datasets.make_blobs(n_samples=200, n_features=6,  centers=4,random_state=0)
 
  data_x.shape,data_y.shape
 
  ((200, 6), (200,))
 
  2.2 训练数据的准备 
  data=np.insert(data_x,data_x.shape[1],data_y,axis=1)
 
  data=pd.DataFrame(data,columns=["F1","F2","F3","F4","F5","F6","target"])
data
 
   
   
   
    
     
      
     F1 
     F2 
     F3 
     F4 
     F5 
     F6 
     target 
     
    
    
     
     0 
     2.116632 
     7.972800 
     -9.328969 
     -8.224605 
     -12.178429 
     5.498447 
     2.0 
     
     
     1 
     1.886449 
     4.621006 
     2.841595 
     0.431245 
     -2.471350 
     2.507833 
     0.0 
     
     
     2 
     2.391329 
     6.464609 
     -9.805900 
     -7.289968 
     -9.650985 
     6.388460 
     2.0 
     
     
     3 
     -1.034776 
     6.626886 
     9.031235 
     -0.812908 
     5.449855 
     0.134062 
     1.0 
     
     
     4 
     -0.481593 
     8.191753 
     7.504717 
     -1.975688 
     6.649021 
     0.636824 
     1.0 
     
     
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     
     
     195 
     5.434893 
     7.128471 
     9.789546 
     6.061382 
     0.634133 
     5.757024 
     3.0 
     
     
     196 
     -0.406625 
     7.586001 
     9.322750 
     -1.837333 
     6.477815 
     -0.992725 
     1.0 
     
     
     197 
     2.031462 
     7.804427 
     -8.539512 
     -9.824409 
     -10.046935 
     6.918085 
     2.0 
     
     
     198 
     4.081889 
     6.127685 
     11.091126 
     4.812011 
     -0.005915 
     5.342211 
     3.0 
     
     
     199 
     0.985744 
     7.285737 
     -8.395940 
     -6.586471 
     -9.651765 
     6.651012 
     2.0 
     
    
   
  200 rows × 7 columns 
  data["target"]=data["target"].astype("int32")
 
  data
 
   
   
   
    
     
      
     F1 
     F2 
     F3 
     F4 
     F5 
     F6 
     target 
     
    
    
     
     0 
     2.116632 
     7.972800 
     -9.328969 
     -8.224605 
     -12.178429 
     5.498447 
     2 
     
     
     1 
     1.886449 
     4.621006 
     2.841595 
     0.431245 
     -2.471350 
     2.507833 
     0 
     
     
     2 
     2.391329 
     6.464609 
     -9.805900 
     -7.289968 
     -9.650985 
     6.388460 
     2 
     
     
     3 
     -1.034776 
     6.626886 
     9.031235 
     -0.812908 
     5.449855 
     0.134062 
     1 
     
     
     4 
     -0.481593 
     8.191753 
     7.504717 
     -1.975688 
     6.649021 
     0.636824 
     1 
     
     
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     
     
     195 
     5.434893 
     7.128471 
     9.789546 
     6.061382 
     0.634133 
     5.757024 
     3 
     
     
     196 
     -0.406625 
     7.586001 
     9.322750 
     -1.837333 
     6.477815 
     -0.992725 
     1 
     
     
     197 
     2.031462 
     7.804427 
     -8.539512 
     -9.824409 
     -10.046935 
     6.918085 
     2 
     
     
     198 
     4.081889 
     6.127685 
     11.091126 
     4.812011 
     -0.005915 
     5.342211 
     3 
     
     
     199 
     0.985744 
     7.285737 
     -8.395940 
     -6.586471 
     -9.651765 
     6.651012 
     2 
     
    
   
  200 rows × 7 columns 
  data.insert(0,"ones",1)
 
  data
 
   
   
   
    
     
      
     ones 
     F1 
     F2 
     F3 
     F4 
     F5 
     F6 
     target 
     
    
    
     
     0 
     1 
     2.116632 
     7.972800 
     -9.328969 
     -8.224605 
     -12.178429 
     5.498447 
     2 
     
     
     1 
     1 
     1.886449 
     4.621006 
     2.841595 
     0.431245 
     -2.471350 
     2.507833 
     0 
     
     
     2 
     1 
     2.391329 
     6.464609 
     -9.805900 
     -7.289968 
     -9.650985 
     6.388460 
     2 
     
     
     3 
     1 
     -1.034776 
     6.626886 
     9.031235 
     -0.812908 
     5.449855 
     0.134062 
     1 
     
     
     4 
     1 
     -0.481593 
     8.191753 
     7.504717 
     -1.975688 
     6.649021 
     0.636824 
     1 
     
     
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     
     
     195 
     1 
     5.434893 
     7.128471 
     9.789546 
     6.061382 
     0.634133 
     5.757024 
     3 
     
     
     196 
     1 
     -0.406625 
     7.586001 
     9.322750 
     -1.837333 
     6.477815 
     -0.992725 
     1 
     
     
     197 
     1 
     2.031462 
     7.804427 
     -8.539512 
     -9.824409 
     -10.046935 
     6.918085 
     2 
     
     
     198 
     1 
     4.081889 
     6.127685 
     11.091126 
     4.812011 
     -0.005915 
     5.342211 
     3 
     
     
     199 
     1 
     0.985744 
     7.285737 
     -8.395940 
     -6.586471 
     -9.651765 
     6.651012 
     2 
     
    
   
  200 rows × 8 columns 
  #第一个类别的数据
data1=data.copy()
data1.loc[data["target"]==0,"target"]=1
data1.loc[data["target"]!=0,"target"]=0
data1
 
   
   
   
    
     
      
     ones 
     F1 
     F2 
     F3 
     F4 
     F5 
     F6 
     target 
     
    
    
     
     0 
     1 
     2.116632 
     7.972800 
     -9.328969 
     -8.224605 
     -12.178429 
     5.498447 
     0 
     
     
     1 
     1 
     1.886449 
     4.621006 
     2.841595 
     0.431245 
     -2.471350 
     2.507833 
     1 
     
     
     2 
     1 
     2.391329 
     6.464609 
     -9.805900 
     -7.289968 
     -9.650985 
     6.388460 
     0 
     
     
     3 
     1 
     -1.034776 
     6.626886 
     9.031235 
     -0.812908 
     5.449855 
     0.134062 
     0 
     
     
     4 
     1 
     -0.481593 
     8.191753 
     7.504717 
     -1.975688 
     6.649021 
     0.636824 
     0 
     
     
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     
     
     195 
     1 
     5.434893 
     7.128471 
     9.789546 
     6.061382 
     0.634133 
     5.757024 
     0 
     
     
     196 
     1 
     -0.406625 
     7.586001 
     9.322750 
     -1.837333 
     6.477815 
     -0.992725 
     0 
     
     
     197 
     1 
     2.031462 
     7.804427 
     -8.539512 
     -9.824409 
     -10.046935 
     6.918085 
     0 
     
     
     198 
     1 
     4.081889 
     6.127685 
     11.091126 
     4.812011 
     -0.005915 
     5.342211 
     0 
     
     
     199 
     1 
     0.985744 
     7.285737 
     -8.395940 
     -6.586471 
     -9.651765 
     6.651012 
     0 
     
    
   
  200 rows × 8 columns 
  data1_x=data1.iloc[:,:data1.shape[1]-1].values
data1_y=data1.iloc[:,data1.shape[1]-1].values
data1_x.shape,data1_y.shape
 
  ((200, 7), (200,))
 
  #第二个类别的数据
data2=data.copy()
data2.loc[data["target"]==1,"target"]=1
data2.loc[data["target"]!=1,"target"]=0
data2
 
   
   
   
    
     
      
     ones 
     F1 
     F2 
     F3 
     F4 
     F5 
     F6 
     target 
     
    
    
     
     0 
     1 
     2.116632 
     7.972800 
     -9.328969 
     -8.224605 
     -12.178429 
     5.498447 
     0 
     
     
     1 
     1 
     1.886449 
     4.621006 
     2.841595 
     0.431245 
     -2.471350 
     2.507833 
     0 
     
     
     2 
     1 
     2.391329 
     6.464609 
     -9.805900 
     -7.289968 
     -9.650985 
     6.388460 
     0 
     
     
     3 
     1 
     -1.034776 
     6.626886 
     9.031235 
     -0.812908 
     5.449855 
     0.134062 
     1 
     
     
     4 
     1 
     -0.481593 
     8.191753 
     7.504717 
     -1.975688 
     6.649021 
     0.636824 
     1 
     
     
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     
     
     195 
     1 
     5.434893 
     7.128471 
     9.789546 
     6.061382 
     0.634133 
     5.757024 
     0 
     
     
     196 
     1 
     -0.406625 
     7.586001 
     9.322750 
     -1.837333 
     6.477815 
     -0.992725 
     1 
     
     
     197 
     1 
     2.031462 
     7.804427 
     -8.539512 
     -9.824409 
     -10.046935 
     6.918085 
     0 
     
     
     198 
     1 
     4.081889 
     6.127685 
     11.091126 
     4.812011 
     -0.005915 
     5.342211 
     0 
     
     
     199 
     1 
     0.985744 
     7.285737 
     -8.395940 
     -6.586471 
     -9.651765 
     6.651012 
     0 
     
    
   
  200 rows × 8 columns 
  data2_x=data2.iloc[:,:data2.shape[1]-1].values
data2_y=data2.iloc[:,data2.shape[1]-1].values
 
  #第三个类别的数据
data3=data.copy()
data3.loc[data["target"]==2,"target"]=1
data3.loc[data["target"]!=2,"target"]=0
data3
 
   
   
   
    
     
      
     ones 
     F1 
     F2 
     F3 
     F4 
     F5 
     F6 
     target 
     
    
    
     
     0 
     1 
     2.116632 
     7.972800 
     -9.328969 
     -8.224605 
     -12.178429 
     5.498447 
     1 
     
     
     1 
     1 
     1.886449 
     4.621006 
     2.841595 
     0.431245 
     -2.471350 
     2.507833 
     0 
     
     
     2 
     1 
     2.391329 
     6.464609 
     -9.805900 
     -7.289968 
     -9.650985 
     6.388460 
     1 
     
     
     3 
     1 
     -1.034776 
     6.626886 
     9.031235 
     -0.812908 
     5.449855 
     0.134062 
     0 
     
     
     4 
     1 
     -0.481593 
     8.191753 
     7.504717 
     -1.975688 
     6.649021 
     0.636824 
     0 
     
     
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     
     
     195 
     1 
     5.434893 
     7.128471 
     9.789546 
     6.061382 
     0.634133 
     5.757024 
     0 
     
     
     196 
     1 
     -0.406625 
     7.586001 
     9.322750 
     -1.837333 
     6.477815 
     -0.992725 
     0 
     
     
     197 
     1 
     2.031462 
     7.804427 
     -8.539512 
     -9.824409 
     -10.046935 
     6.918085 
     1 
     
     
     198 
     1 
     4.081889 
     6.127685 
     11.091126 
     4.812011 
     -0.005915 
     5.342211 
     0 
     
     
     199 
     1 
     0.985744 
     7.285737 
     -8.395940 
     -6.586471 
     -9.651765 
     6.651012 
     1 
     
    
   
  200 rows × 8 columns 
  data3_x=data3.iloc[:,:data3.shape[1]-1].values
data3_y=data3.iloc[:,data3.shape[1]-1].values
 
  #第四个类别的数据
data4=data.copy()
data4.loc[data["target"]==3,"target"]=1
data4.loc[data["target"]!=3,"target"]=0
data4
 
   
   
   
    
     
      
     ones 
     F1 
     F2 
     F3 
     F4 
     F5 
     F6 
     target 
     
    
    
     
     0 
     1 
     2.116632 
     7.972800 
     -9.328969 
     -8.224605 
     -12.178429 
     5.498447 
     0 
     
     
     1 
     1 
     1.886449 
     4.621006 
     2.841595 
     0.431245 
     -2.471350 
     2.507833 
     0 
     
     
     2 
     1 
     2.391329 
     6.464609 
     -9.805900 
     -7.289968 
     -9.650985 
     6.388460 
     0 
     
     
     3 
     1 
     -1.034776 
     6.626886 
     9.031235 
     -0.812908 
     5.449855 
     0.134062 
     0 
     
     
     4 
     1 
     -0.481593 
     8.191753 
     7.504717 
     -1.975688 
     6.649021 
     0.636824 
     0 
     
     
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     ... 
     
     
     195 
     1 
     5.434893 
     7.128471 
     9.789546 
     6.061382 
     0.634133 
     5.757024 
     1 
     
     
     196 
     1 
     -0.406625 
     7.586001 
     9.322750 
     -1.837333 
     6.477815 
     -0.992725 
     0 
     
     
     197 
     1 
     2.031462 
     7.804427 
     -8.539512 
     -9.824409 
     -10.046935 
     6.918085 
     0 
     
     
     198 
     1 
     4.081889 
     6.127685 
     11.091126 
     4.812011 
     -0.005915 
     5.342211 
     1 
     
     
     199 
     1 
     0.985744 
     7.285737 
     -8.395940 
     -6.586471 
     -9.651765 
     6.651012 
     0 
     
    
   
  200 rows × 8 columns 
  data4_x=data4.iloc[:,:data4.shape[1]-1].values
data4_y=data4.iloc[:,data4.shape[1]-1].values
 
  2.3 定义假设函数、代价函数和梯度下降算法 
  def sigmoid(z):
    return 1 / (1 + np.exp(-z))
 
  def h(X,w):
    z=X@w
    h=sigmoid(z)
    return h
 
  #代价函数构造
def cost(X,w,y):
    #当X(m,n+1),y(m,),w(n+1,1)
    y_hat=sigmoid(X@w)
    right=np.multiply(y.ravel(),np.log(y_hat).ravel())+np.multiply((1-y).ravel(),np.log(1-y_hat).ravel())
    cost=-np.sum(right)/X.shape[0]
    return cost
 
  def grandient(X,y,iter_num,alpha):
    y=y.reshape((X.shape[0],1))
    w=np.zeros((X.shape[1],1))
    cost_lst=[]  
    for i in range(iter_num):
        y_pred=h(X,w)-y
        temp=np.zeros((X.shape[1],1))
        for j in range(X.shape[1]):
            right=np.multiply(y_pred.ravel(),X[:,j])
            
            gradient=1/(X.shape[0])*(np.sum(right))
            temp[j,0]=w[j,0]-alpha*gradient
        w=temp
        cost_lst.append(cost(X,w,y.ravel()))
    return w,cost_lst
 
  2.4 学习这四个分类模型 
  import matplotlib.pyplot as plt
 
  #初始化超参数
iter_num,alpha=600000,0.001
 
  #训练第1个模型
w1,cost_lst1=grandient(data1_x,data1_y,iter_num,alpha)
 
  plt.plot(range(iter_num),cost_lst1,"b-o")
 
  []
 
   
  #训练第2个模型
w2,cost_lst2=grandient(data2_x,data2_y,iter_num,alpha)
plt.plot(range(iter_num),cost_lst2,"b-o")
 
  []
 
   
  #训练第3个模型
w3,cost_lst3=grandient(data3_x,data3_y,iter_num,alpha)
plt.plot(range(iter_num),cost_lst3,"b-o")
 
  []
 
   
  #训练第4个模型
w4,cost_lst4=grandient(data4_x,data4_y,iter_num,alpha)
plt.plot(range(iter_num),cost_lst4,"b-o")
 
  []
 
   
  2.5 利用模型进行预测 
  data_x
 
  array([[ 2.11663151e+00,  7.97280013e+00, -9.32896918e+00,
        -8.22460526e+00, -1.21784287e+01,  5.49844655e+00],
       [ 1.88644899e+00,  4.62100554e+00,  2.84159548e+00,
         4.31244563e-01, -2.47135027e+00,  2.50783257e+00],
       [ 2.39132949e+00,  6.46460915e+00, -9.80590050e+00,
        -7.28996786e+00, -9.65098460e+00,  6.38845956e+00],
       ...,
       [ 2.03146167e+00,  7.80442707e+00, -8.53951210e+00,
        -9.82440872e+00, -1.00469351e+01,  6.91808489e+00],
       [ 4.08188906e+00,  6.12768483e+00,  1.10911262e+01,
         4.81201082e+00, -5.91530191e-03,  5.34221079e+00],
       [ 9.85744105e-01,  7.28573657e+00, -8.39593964e+00,
        -6.58647097e+00, -9.65176507e+00,  6.65101187e+00]])
 
  data_x=np.insert(data_x,0,1,axis=1)
 
  data_x.shape
 
  (200, 7)
 
  w3.shape
 
  (7, 1)
 
  multi_pred=pd.DataFrame(zip(h(data_x,w1).ravel(),h(data_x,w2).ravel(),h(data_x,w3).ravel(),h(data_x,w4).ravel()))
multi_pred
 
   
   
   
    
     
      
     0 
     1 
     2 
     3 
     
    
    
     
     0 
     0.020436 
     4.556248e-15 
     9.999975e-01 
     2.601227e-27 
     
     
     1 
     0.820488 
     4.180906e-05 
     3.551499e-05 
     5.908691e-05 
     
     
     2 
     0.109309 
     7.316201e-14 
     9.999978e-01 
     7.091713e-24 
     
     
     3 
     0.036608 
     9.999562e-01 
     1.048562e-09 
     5.724854e-03 
     
     
     4 
     0.003075 
     9.999292e-01 
     2.516742e-09 
     6.423038e-05 
     
     
     ... 
     ... 
     ... 
     ... 
     ... 
     
     
     195 
     0.017278 
     3.221293e-06 
     3.753372e-14 
     9.999943e-01 
     
     
     196 
     0.003369 
     9.999966e-01 
     6.673394e-10 
     2.281428e-03 
     
     
     197 
     0.000606 
     1.118174e-13 
     9.999941e-01 
     1.780212e-28 
     
     
     198 
     0.013072 
     4.999118e-05 
     9.811154e-14 
     9.996689e-01 
     
     
     199 
     0.151548 
     1.329623e-13 
     9.999447e-01 
     2.571989e-24 
     
    
   
  200 rows × 4 columns 
  2.6 计算准确率 
  np.sum(np.argmax(multi_pred.values,axis=1)==data_y.ravel())/len(data)
 
  1.0

	F1	F2	F3	F4	target
0	5.1	3.5	1.4	0.2	0.0
1	4.9	3.0	1.4	0.2	0.0
2	4.7	3.2	1.3	0.2	0.0
3	4.6	3.1	1.5	0.2	0.0
4	5.0	3.6	1.4	0.2	0.0
...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	2.0
146	6.3	2.5	5.0	1.9	2.0
147	6.5	3.0	5.2	2.0	2.0
148	6.2	3.4	5.4	2.3	2.0
149	5.9	3.0	5.1	1.8	2.0

	ones	F1	F2	F3	F4	target
0	1	5.1	3.5	1.4	0.2	0.0
1	1	4.9	3.0	1.4	0.2	0.0
2	1	4.7	3.2	1.3	0.2	0.0
3	1	4.6	3.1	1.5	0.2	0.0
4	1	5.0	3.6	1.4	0.2	0.0
...	...	...	...	...	...	...
145	1	6.7	3.0	5.2	2.3	2.0
146	1	6.3	2.5	5.0	1.9	2.0
147	1	6.5	3.0	5.2	2.0	2.0
148	1	6.2	3.4	5.4	2.3	2.0
149	1	5.9	3.0	5.1	1.8	2.0

	ones	F1	F2	F3	F4	target
0	1	5.1	3.5	1.4	0.2	0
1	1	4.9	3.0	1.4	0.2	0
2	1	4.7	3.2	1.3	0.2	0
3	1	4.6	3.1	1.5	0.2	0
4	1	5.0	3.6	1.4	0.2	0
...	...	...	...	...	...	...
145	1	6.7	3.0	5.2	2.3	2
146	1	6.3	2.5	5.0	1.9	2
147	1	6.5	3.0	5.2	2.0	2
148	1	6.2	3.4	5.4	2.3	2
149	1	5.9	3.0	5.1	1.8	2

	ones	F1	F2	F3	F4	target
0	1	5.1	3.5	1.4	0.2	0
1	1	4.9	3.0	1.4	0.2	0
2	1	4.7	3.2	1.3	0.2	0
3	1	4.6	3.1	1.5	0.2	0
4	1	5.0	3.6	1.4	0.2	0
...	...	...	...	...	...	...
145	1	6.7	3.0	5.2	2.3	2
146	1	6.3	2.5	5.0	1.9	2
147	1	6.5	3.0	5.2	2.0	2
148	1	6.2	3.4	5.4	2.3	2
149	1	5.9	3.0	5.1	1.8	2

	ones	F1	F2	F3	F4	target
0	1	5.1	3.5	1.4	0.2	1
1	1	4.9	3.0	1.4	0.2	1
2	1	4.7	3.2	1.3	0.2	1
3	1	4.6	3.1	1.5	0.2	1
4	1	5.0	3.6	1.4	0.2	1
...	...	...	...	...	...	...
145	1	6.7	3.0	5.2	2.3	0
146	1	6.3	2.5	5.0	1.9	0
147	1	6.5	3.0	5.2	2.0	0
148	1	6.2	3.4	5.4	2.3	0
149	1	5.9	3.0	5.1	1.8	0

	ones	F1	F2	F3	F4	target
50	1	7.0	3.2	4.7	1.4	1
51	1	6.4	3.2	4.5	1.5	1
52	1	6.9	3.1	4.9	1.5	1
53	1	5.5	2.3	4.0	1.3	1
54	1	6.5	2.8	4.6	1.5	1

	ones	F1	F2	F3	F4	target
0	1	5.1	3.5	1.4	0.2	0
1	1	4.9	3.0	1.4	0.2	0
2	1	4.7	3.2	1.3	0.2	0
3	1	4.6	3.1	1.5	0.2	0
4	1	5.0	3.6	1.4	0.2	0
...	...	...	...	...	...	...
145	1	6.7	3.0	5.2	2.3	1
146	1	6.3	2.5	5.0	1.9	1
147	1	6.5	3.0	5.2	2.0	1
148	1	6.2	3.4	5.4	2.3	1
149	1	5.9	3.0	5.1	1.8	1

	0	1	2
0	0.999297	0.108037	1.484454e-11
1	0.997061	0.270814	1.723440e-10
2	0.998633	0.164710	1.027982e-10
3	0.995774	0.231910	5.819755e-10
4	0.999415	0.085259	1.484347e-11
...	...	...	...
145	0.000007	0.127574	9.620405e-01
146	0.000006	0.496389	9.522146e-01
147	0.000010	0.234745	8.969022e-01
148	0.000006	0.058444	9.902009e-01
149	0.000014	0.284295	9.287852e-01

	模型1	模糊2	模型3
0	1	0	0
1	1	0	0
2	1	0	0
3	1	0	0
4	1	0	0
...	...	...	...
145	0	0	1
146	0	1	1
147	0	0	1
148	0	0	1
149	0	0	1

	F1	F2	F3	F4	F5	F6	target
0	2.116632	7.972800	-9.328969	-8.224605	-12.178429	5.498447	2.0
1	1.886449	4.621006	2.841595	0.431245	-2.471350	2.507833	0.0
2	2.391329	6.464609	-9.805900	-7.289968	-9.650985	6.388460	2.0
3	-1.034776	6.626886	9.031235	-0.812908	5.449855	0.134062	1.0
4	-0.481593	8.191753	7.504717	-1.975688	6.649021	0.636824	1.0
...	...	...	...	...	...	...	...
195	5.434893	7.128471	9.789546	6.061382	0.634133	5.757024	3.0
196	-0.406625	7.586001	9.322750	-1.837333	6.477815	-0.992725	1.0
197	2.031462	7.804427	-8.539512	-9.824409	-10.046935	6.918085	2.0
198	4.081889	6.127685	11.091126	4.812011	-0.005915	5.342211	3.0
199	0.985744	7.285737	-8.395940	-6.586471	-9.651765	6.651012	2.0

	F1	F2	F3	F4	F5	F6	target
0	2.116632	7.972800	-9.328969	-8.224605	-12.178429	5.498447	2
1	1.886449	4.621006	2.841595	0.431245	-2.471350	2.507833	0
2	2.391329	6.464609	-9.805900	-7.289968	-9.650985	6.388460	2
3	-1.034776	6.626886	9.031235	-0.812908	5.449855	0.134062	1
4	-0.481593	8.191753	7.504717	-1.975688	6.649021	0.636824	1
...	...	...	...	...	...	...	...
195	5.434893	7.128471	9.789546	6.061382	0.634133	5.757024	3
196	-0.406625	7.586001	9.322750	-1.837333	6.477815	-0.992725	1
197	2.031462	7.804427	-8.539512	-9.824409	-10.046935	6.918085	2
198	4.081889	6.127685	11.091126	4.812011	-0.005915	5.342211	3
199	0.985744	7.285737	-8.395940	-6.586471	-9.651765	6.651012	2

	ones	F1	F2	F3	F4	F5	F6	target
0	1	2.116632	7.972800	-9.328969	-8.224605	-12.178429	5.498447	2
1	1	1.886449	4.621006	2.841595	0.431245	-2.471350	2.507833	0
2	1	2.391329	6.464609	-9.805900	-7.289968	-9.650985	6.388460	2
3	1	-1.034776	6.626886	9.031235	-0.812908	5.449855	0.134062	1
4	1	-0.481593	8.191753	7.504717	-1.975688	6.649021	0.636824	1
...	...	...	...	...	...	...	...	...
195	1	5.434893	7.128471	9.789546	6.061382	0.634133	5.757024	3
196	1	-0.406625	7.586001	9.322750	-1.837333	6.477815	-0.992725	1
197	1	2.031462	7.804427	-8.539512	-9.824409	-10.046935	6.918085	2
198	1	4.081889	6.127685	11.091126	4.812011	-0.005915	5.342211	3
199	1	0.985744	7.285737	-8.395940	-6.586471	-9.651765	6.651012	2

	ones	F1	F2	F3	F4	F5	F6	target
0	1	2.116632	7.972800	-9.328969	-8.224605	-12.178429	5.498447	0
1	1	1.886449	4.621006	2.841595	0.431245	-2.471350	2.507833	1
2	1	2.391329	6.464609	-9.805900	-7.289968	-9.650985	6.388460	0
3	1	-1.034776	6.626886	9.031235	-0.812908	5.449855	0.134062	0
4	1	-0.481593	8.191753	7.504717	-1.975688	6.649021	0.636824	0
...	...	...	...	...	...	...	...	...
195	1	5.434893	7.128471	9.789546	6.061382	0.634133	5.757024	0
196	1	-0.406625	7.586001	9.322750	-1.837333	6.477815	-0.992725	0
197	1	2.031462	7.804427	-8.539512	-9.824409	-10.046935	6.918085	0
198	1	4.081889	6.127685	11.091126	4.812011	-0.005915	5.342211	0
199	1	0.985744	7.285737	-8.395940	-6.586471	-9.651765	6.651012	0

	ones	F1	F2	F3	F4	F5	F6	target
0	1	2.116632	7.972800	-9.328969	-8.224605	-12.178429	5.498447	0
1	1	1.886449	4.621006	2.841595	0.431245	-2.471350	2.507833	0
2	1	2.391329	6.464609	-9.805900	-7.289968	-9.650985	6.388460	0
3	1	-1.034776	6.626886	9.031235	-0.812908	5.449855	0.134062	1
4	1	-0.481593	8.191753	7.504717	-1.975688	6.649021	0.636824	1
...	...	...	...	...	...	...	...	...
195	1	5.434893	7.128471	9.789546	6.061382	0.634133	5.757024	0
196	1	-0.406625	7.586001	9.322750	-1.837333	6.477815	-0.992725	1
197	1	2.031462	7.804427	-8.539512	-9.824409	-10.046935	6.918085	0
198	1	4.081889	6.127685	11.091126	4.812011	-0.005915	5.342211	0
199	1	0.985744	7.285737	-8.395940	-6.586471	-9.651765	6.651012	0

	ones	F1	F2	F3	F4	F5	F6	target
0	1	2.116632	7.972800	-9.328969	-8.224605	-12.178429	5.498447	1
1	1	1.886449	4.621006	2.841595	0.431245	-2.471350	2.507833	0
2	1	2.391329	6.464609	-9.805900	-7.289968	-9.650985	6.388460	1
3	1	-1.034776	6.626886	9.031235	-0.812908	5.449855	0.134062	0
4	1	-0.481593	8.191753	7.504717	-1.975688	6.649021	0.636824	0
...	...	...	...	...	...	...	...	...
195	1	5.434893	7.128471	9.789546	6.061382	0.634133	5.757024	0
196	1	-0.406625	7.586001	9.322750	-1.837333	6.477815	-0.992725	0
197	1	2.031462	7.804427	-8.539512	-9.824409	-10.046935	6.918085	1
198	1	4.081889	6.127685	11.091126	4.812011	-0.005915	5.342211	0
199	1	0.985744	7.285737	-8.395940	-6.586471	-9.651765	6.651012	1

	ones	F1	F2	F3	F4	F5	F6	target
0	1	2.116632	7.972800	-9.328969	-8.224605	-12.178429	5.498447	0
1	1	1.886449	4.621006	2.841595	0.431245	-2.471350	2.507833	0
2	1	2.391329	6.464609	-9.805900	-7.289968	-9.650985	6.388460	0
3	1	-1.034776	6.626886	9.031235	-0.812908	5.449855	0.134062	0
4	1	-0.481593	8.191753	7.504717	-1.975688	6.649021	0.636824	0
...	...	...	...	...	...	...	...	...
195	1	5.434893	7.128471	9.789546	6.061382	0.634133	5.757024	1
196	1	-0.406625	7.586001	9.322750	-1.837333	6.477815	-0.992725	0
197	1	2.031462	7.804427	-8.539512	-9.824409	-10.046935	6.918085	0
198	1	4.081889	6.127685	11.091126	4.812011	-0.005915	5.342211	1
199	1	0.985744	7.285737	-8.395940	-6.586471	-9.651765	6.651012	0

	0	1	2	3
0	0.020436	4.556248e-15	9.999975e-01	2.601227e-27
1	0.820488	4.180906e-05	3.551499e-05	5.908691e-05
2	0.109309	7.316201e-14	9.999978e-01	7.091713e-24
3	0.036608	9.999562e-01	1.048562e-09	5.724854e-03
4	0.003075	9.999292e-01	2.516742e-09	6.423038e-05
...	...	...	...	...
195	0.017278	3.221293e-06	3.753372e-14	9.999943e-01
196	0.003369	9.999966e-01	6.673394e-10	2.281428e-03
197	0.000606	1.118174e-13	9.999941e-01	1.780212e-28
198	0.013072	4.999118e-05	9.811154e-14	9.996689e-01
199	0.151548	1.329623e-13	9.999447e-01	2.571989e-24

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
理解Gunicorn：Python WSGI服务器的基石范范0825 ipython linux 运维
理解Gunicorn：PythonWSGI服务器的基石介绍Gunicorn，全称GreenUnicorn，是一个为PythonWSGI（WebServerGatewayInterface）应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具，Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置，帮助初学者快速上手。1.什么是Gunico
Python数据分析与可视化实战指南 William数据分析 python python 数据
在数据驱动的时代，Python因其简洁的语法、强大的库生态系统以及活跃的社区，成为了数据分析与可视化的首选语言。本文将通过一个详细的案例，带领大家学习如何使用Python进行数据分析，并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前，我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
2022-07-08 保利学府里李楚怡1307022
——保利碧桂园学府里——童梦奇趣【科学实验室】「7.9-7.10」✏玩出大智慧约99-144㎡二期全新升级力作
python os.environ 江湖偌大 python 深度学习
os.environ['TF_CPP_MIN_LOG_LEVEL']='0'#默认值，输出所有信息os.environ['TF_CPP_MIN_LOG_LEVEL']='1'#屏蔽通知信息（INFO）os.environ['TF_CPP_MIN_LOG_LEVEL']='2'#屏蔽通知信息和警告信息（INFO\WARNING）os.environ['TF_CPP_MIN_LOG_LEVEL']='
Python中os.environ基本介绍及使用方法鹤冲天Pro #Python python 服务器开发语言
文章目录python中os.environos.environ简介os.environ进行环境变量的增删改查python中os.environ的使用详解1.简介2.key字段详解2.1常见key字段3.os.environ.get()用法4.环境变量的增删改查和判断是否存在4.1新增环境变量4.2更新环境变量4.3获取环境变量4.4删除环境变量4.5判断环境变量是否存在python中os.envi
Pyecharts数据可视化大屏：打造沉浸式数据分析体验我的运维人生信息可视化数据分析数据挖掘运维开发技术共享
Pyecharts数据可视化大屏：打造沉浸式数据分析体验在当今这个数据驱动的时代，如何将海量数据以直观、生动的方式展现出来，成为了数据分析师和企业决策者关注的焦点。Pyecharts，作为一款基于Python的开源数据可视化库，凭借其丰富的图表类型、灵活的配置选项以及高度的定制化能力，成为了构建数据可视化大屏的理想选择。本文将深入探讨如何利用Pyecharts打造数据可视化大屏，并通过实际代码案例
Python教程：一文了解使用Python处理XPath 旦莫 Python进阶 python 开发语言
目录1.环境准备1.1安装lxml1.2验证安装2.XPath基础2.1什么是XPath？2.2XPath语法2.3示例XML文档3.使用lxml解析XML3.1解析XML文档3.2查看解析结果4.XPath查询4.1基本路径查询4.2使用属性查询4.3查询多个节点5.XPath的高级用法5.1使用逻辑运算符5.2使用函数6.实战案例6.1从网页抓取数据6.1.1安装Requests库6.1.2代
python os.environ_python os.environ 读取和设置环境变量 weixin_39605414 python os.environ
>>>importos>>>os.environ.keys()['LC_NUMERIC','GOPATH','GOROOT','GOBIN','LESSOPEN','SSH_CLIENT','LOGNAME','USER','HOME','LC_PAPER','PATH','DISPLAY','LANG','TERM','SHELL','J2REDIR','LC_MONETARY','QT_QPA
使用Faiss进行高效相似度搜索 llzwxh888 faiss python
在现代AI应用中，快速和高效的相似度搜索是至关重要的。Faiss（FacebookAISimilaritySearch）是一个专门用于快速相似度搜索和聚类的库，特别适用于高维向量。本文将介绍如何使用Faiss来进行相似度搜索，并结合Python代码演示其基本用法。什么是Faiss？Faiss是一个由FacebookAIResearch团队开发的开源库，主要用于高维向量的相似性搜索和聚类。Faiss
python是什么意思中文-在python中%是什么意思编程大乐趣
Python中%有两种：1、数值运算：%代表取模，返回除法的余数。如：>>>7%212、%操作符（字符串格式化，stringformatting），说明如下：%[(name)][flags][width].[precision]typecode(name)为命名flags可以有+，-，''或0。+表示右对齐。-表示左对齐。''为一个空格，表示在正数的左侧填充一个空格，从而与负数对齐。0表示使用0填
Day1笔记-Python简介&标识符和关键字&输入输出 ~在杰难逃~ Python python 开发语言大数据数据分析数据挖掘
大家好，从今天开始呢，杰哥开展一个新的专栏，当然，数据分析部分也会不定时更新的，这个新的专栏主要是讲解一些Python的基础语法和知识，帮助0基础的小伙伴入门和学习Python，感兴趣的小伙伴可以开始认真学习啦！一、Python简介【了解】1.计算机工作原理编程语言就是用来定义计算机程序的形式语言。我们通过编程语言来编写程序代码，再通过语言处理程序执行向计算机发送指令，让计算机完成对应的工作，编程
python八股文面试题分享及解析(1) Shawn________ python
#1.'''a=1b=2不用中间变量交换a和b'''#1.a=1b=2a,b=b,aprint(a)print(b)结果：21#2.ll=[]foriinrange(3):ll.append({'num':i})print(11)结果:#[{'num':0},{'num':1},{'num':2}]#3.kk=[]a={'num':0}foriinrange(3):#0,12#可变类型，不仅仅改变
每日算法&面试题，大厂特训二十八天——第二十天（树）肥学 ⚡算法题⚡面试题每日精进 java 算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
Python快速入门 —— 第三节：类与对象孤华暗香 Python快速入门 python 开发语言
第三节：类与对象目标：了解面向对象编程的基础概念，并学会如何定义类和创建对象。内容：类与对象：定义类：class关键字。类的构造函数：__init__()。类的属性和方法。对象的创建与使用。示例：classStudent:def__init__(self,name,age,major):self.name&#
pyecharts——绘制柱形图折线图 2224070247 信息可视化 python java 数据可视化
一、pyecharts概述自2013年6月百度EFE(ExcellentFrontEnd）数据可视化团队研发的ECharts1.0发布到GitHub网站以来，ECharts一直备受业界权威的关注并获得广泛好评，成为目前成熟且流行的数据可视化图表工具，被应用到诸多数据可视化的开发领域。Python作为数据分析领域最受欢迎的语言，也加入ECharts的使用行列，并研发出方便Python开发者使用的数据
番茄西红柿叶子病害分类数据集12882张11类别 futureflsl 数据集分类数据挖掘人工智能
数据集类型：图像分类用，不可用于目标检测无标注文件数据集格式：仅仅包含jpg图片，每个类别文件夹下面存放着对应图片图片数量(jpg文件个数)：12882分类类别数：11类别名称:["Bacterial_Spot_Bacteria","Early_Blight_Fungus","Healthy","Late_Blight_Water_Mold","Leaf_Mold_Fungus","Powdery
Python 实现图片裁剪（附代码） | Python工具剑客阿良_ALiang
前言本文提供将图片按照自定义尺寸进行裁剪的工具方法，一如既往的实用主义。环境依赖ffmpeg环境安装，可以参考我的另一篇文章：windowsffmpeg安装部署_阿良的博客-CSDN博客本文主要使用到的不是ffmpeg，而是ffprobe也在上面这篇文章中的zip包中。ffmpy安装：pipinstallffmpy-ihttps://pypi.douban.com/simple代码不废话了，上代码
【华为OD技术面试真题 - 技术面】- python八股文真题题库（4) 算法大师华为od 面试 python
华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选**1.Python中的`with`**用途和功能自动资源管理示例：文件操作上下文管理协议示例代码工作流程解析优点2.\_\_new\_\_和**\_\_init\_\_**区别__new____init__区别总结3.**切片（Slicing）操作**基本切片语法
python os 环境变量 CV矿工 python 开发语言 numpy
环境变量：环境变量是程序和操作系统之间的通信方式。有些字符不宜明文写进代码里，比如数据库密码，个人账户密码，如果写进自己本机的环境变量里，程序用的时候通过os.environ.get（）取出来就行了。os.environ是一个环境变量的字典。环境变量的相关操作importos"""设置/修改环境变量：os.environ[‘环境变量名称’]=‘环境变量值’#其中key和value均为string类
Python爬虫解析工具之xpath使用详解 eqa11 python 爬虫开发语言
文章目录Python爬虫解析工具之xpath使用详解一、引言二、环境准备1、插件安装2、依赖库安装三、xpath语法详解1、路径表达式2、通配符3、谓语4、常用函数四、xpath在Python代码中的使用1、文档树的创建2、使用xpath表达式3、获取元素内容和属性五、总结Python爬虫解析工具之xpath使用详解一、引言在Python爬虫开发中，数据提取是一个至关重要的环节。xpath作为一门
【华为OD技术面试真题 - 技术面】- python八股文真题题库（1）算法大师华为od 面试 python
华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选1.数据预处理流程数据预处理的主要步骤工具和库2.介绍线性回归、逻辑回归模型线性回归（LinearRegression）模型形式：关键点：逻辑回归（LogisticRegression）模型形式：关键点：参数估计与评估：3.python浅拷贝及深拷贝浅拷贝（Shal
数字里的世界17期：2021年全球10大顶级数据中心，中国移动榜首张三叨
你知道吗？2016年，全球的数据中心共计用电4160亿千瓦时，比整个英国的发电量还多40％！前言每天，我们都会创造超过250万TB的数据。并且随着物联网（IOT）的不断普及，这一数据将持续增长。如此庞大的数据被存储在被称为“数据中心”的专用设施中。虽然最早的数据中心建于20世纪40年代，但直到1997-2000年的互联网泡沫期间才逐渐成为主流。当前人类的技术，比如人工智能和机器学习，已经将我们推向
nosql数据库技术与应用知识点皆过客，揽星河 NoSQL nosql 数据库大数据数据分析数据结构非关系型数据库
Nosql知识回顾大数据处理流程数据采集(flume、爬虫、传感器)数据存储(本门课程NoSQL所处的阶段)Hdfs、MongoDB、HBase等数据清洗(入仓)Hive等数据处理、分析(Spark、Flink等)数据可视化数据挖掘、机器学习应用(Python、SparkMLlib等)大数据时代存储的挑战(三高)高并发(同一时间很多人访问)高扩展(要求随时根据需求扩展存储)高效率(要求读写速度快)
《Python数据分析实战终极指南》 xjt921122 python 数据分析开发语言
对于分析师来说，大家在学习Python数据分析的路上，多多少少都遇到过很多大坑**，有关于技能和思维的**：Excel已经没办法处理现有的数据量了，应该学Python吗？找了一大堆Python和Pandas的资料来学习，为什么自己动手就懵了？跟着比赛类公开数据分析案例练了很久，为什么当自己面对数据需求还是只会数据处理而没有分析思路？学了对比、细分、聚类分析，也会用PEST、波特五力这类分析法，为啥
Python中深拷贝与浅拷贝的区别 yuxiaoyu.
转自：http://blog.csdn.net/u014745194/article/details/70271868定义：在Python中对象的赋值其实就是对象的引用。当创建一个对象，把它赋值给另一个变量的时候，python并没有拷贝这个对象，只是拷贝了这个对象的引用而已。浅拷贝：拷贝了最外围的对象本身，内部的元素都只是拷贝了一个引用而已。也就是，把对象复制一遍，但是该对象中引用的其他对象我不复
Python开发常用的三方模块如下：换个网名有点难 python 开发语言
Python是一门功能强大的编程语言，拥有丰富的第三方库，这些库为开发者提供了极大的便利。以下是100个常用的Python库，涵盖了多个领域：1、NumPy，用于科学计算的基础库。2、Pandas，提供数据结构和数据分析工具。3、Matplotlib，一个绘图库。4、Scikit-learn，机器学习库。5、SciPy，用于数学、科学和工程的库。6、TensorFlow，由Google开发的开源机
Python编译器鹿鹿~ Python编译器 Python python 开发语言后端
嘿嘿嘿我又来了啊有些小盆友可能不知道Python其实是有编译器的，也就是PyCharm。你们可能会问到这个是干嘛的又不可以吃也不可以穿好像没有什么用，其实你还说对了这个还真的不可以吃也不可以穿，但是它用来干嘛的呢。用来编译你所打出的代码进行运行（可能这里说的有点不对但是只是个人认为）现在我们来说说PyCharm是用来干嘛的。PyCharm是一种PythonIDE，带有一整套可以帮助用户在使用Pyt
xilinx vivado PULLMODE 设置思路坚持每天写程序 fpga开发
1.xilinx引脚分类XilinxIO的分类：以XC7A100TFGG484为例，其引脚分类如下：1.UserIO(用户IO)：用户使用的普通IO1.1专用(Dedicated)IO：命名为IO_LXXY_#、IO_XX_#的引脚，有固定的特定用途，多为底层特定功能的直接实现，如差分对信号、关键控制信号等，不能随意变更。1.2多功能(Multi-Function)IO：命名为IO_LXXY_ZZ
为什么瘦子很难增胖？我的狗毛毛
我是个标准的瘦子，168，100斤。用一句通俗的话来讲，我连马甲线都瘦出来了（体脂含量比较低）。但是我反而很羡慕那些比较丰满的女人，我的理想是再增重十五斤，练成前凸后翘的魔鬼身材。为此我开始纠正自己不规律的作息，吃高热量的食物，减少运动量，能坐着绝不站着，能躺着绝不坐着。但是结果却没有丝毫变化。我一直很苦恼，直到最近在网上看到一个视频，英国的某个研究机构做了一个实验，想要知道瘦子能否在高热量的食物
深入浅出Java Annotation(元注解和自定义注解） Josh_Persistence Java Annotation 元注解自定义注解
一、基本概述　　 Annontation是Java5开始引入的新特征。中文名称一般叫注解。它提供了一种安全的类似注释的机制，用来将任何的信息或元数据（metadata）与程序元素（类、方法、成员变量等）进行关联。　　更通俗的意思是为程序的元素（类、方法、成员变量）加上更直观更明了的说明，这些说明信息是与程序的业务逻辑无关，并且是供指定的工具或
mysql优化特定类型的查询 annan211 java 工作 mysql
本节所介绍的查询优化的技巧都是和特定版本相关的，所以对于未来mysql的版本未必适用。 1 优化count查询对于count这个函数的网上的大部分资料都是错误的或者是理解的都是一知半解的。在做优化之前我们先来看看真正的count()函数的作用到底是什么。 count()是一个特殊的函数，有两种非常不同的作用，他可以统计某个列值的数量，也可以统计行数。在统
MAC下安装多版本JDK和切换几种方式棋子chessman jdk
环境： MAC AIR,OS X 10.10,64位历史：过去 Mac 上的 Java 都是由 Apple 自己提供，只支持到 Java 6，并且OS X 10.7 开始系统并不自带（而是可选安装）（原自带的是1.6）。后来 Apple 加入 OpenJDK 继续支持 Java 6，而 Java 7 将由 Oracle 负责提供。在终端中输入jav
javaScript （1） Array_06 JavaScript java 浏览器
JavaScript 1、运算符　　运算符就是完成操作的一系列符号，它有七类：　　赋值运算符（=,+=,-=,*=,/=,%=,<<=,>>=,|=,&=）、算术运算符(+,-,*,/,++,--,%)、比较运算符(>,<,<=,>=,==,===,!=,!==)、逻辑运算符(||,&&,!)、条件运算(?:)、位
国内顶级代码分享网站袁潇含 java jdk oracle .net PHP
现在国内很多开源网站感觉都是为了利益而做的当然利益是肯定的,否则谁也不会免费的去做网站 &
Elasticsearch、MongoDB和Hadoop比较随意而生 mongodb hadoop 搜索引擎
IT界在过去几年中出现了一个有趣的现象。很多新的技术出现并立即拥抱了“大数据”。稍微老一点的技术也会将大数据添进自己的特性，避免落大部队太远，我们看到了不同技术之间的边际的模糊化。假如你有诸如Elasticsearch或者Solr这样的搜索引擎，它们存储着JSON文档，MongoDB存着JSON文档，或者一堆JSON文档存放在一个Hadoop集群的HDFS中。你可以使用这三种配
mac os 系统科研软件总结张亚雄 mac os
1.1 Microsoft Office for Mac 2011 大客户版，自行搜索。 1.2 Latex （MacTex）: 系统环境：https://tug.org/mactex/ &nb
Maven实战（四）生命周期 AdyZhang maven
1. 三套生命周期 Maven拥有三套相互独立的生命周期，它们分别为clean，default和site。每个生命周期包含一些阶段，这些阶段是有顺序的，并且后面的阶段依赖于前面的阶段，用户和Maven最直接的交互方式就是调用这些生命周期阶段。以clean生命周期为例，它包含的阶段有pre-clean, clean 和 post
Linux下Jenkins迁移 aijuans Jenkins
1. 将Jenkins程序目录copy过去源程序在/export/data/tomcatRoot/ofctest-jenkins.jd.com下面 tar -cvzf jenkins.tar.gz ofctest-jenkins.jd.com &
request.getInputStream()只能获取一次的问题 ayaoxinchao request Inputstream
问题：在使用HTTP协议实现应用间接口通信时，服务端读取客户端请求过来的数据，会用到request.getInputStream()，第一次读取的时候可以读取到数据，但是接下来的读取操作都读取不到数据原因： 1. 一个InputStream对象在被读取完成后，将无法被再次读取，始终返回-1； 2. InputStream并没有实现reset方法（可以重
数据库SQL优化大总结之百万级数据库优化方案 BigBird2012 SQL优化
网上关于SQL优化的教程很多，但是比较杂乱。近日有空整理了一下，写出来跟大家分享一下，其中有错误和不足的地方，还请大家纠正补充。这篇文章我花费了大量的时间查找资料、修改、排版，希望大家阅读之后，感觉好的话推荐给更多的人，让更多的人看到、纠正以及补充。 1.对查询进行优化，要尽量避免全表扫描，首先应考虑在 where 及 order by 涉及的列上建立索引。 2.应尽量避免在 where
jsonObject的使用 bijian1013 java json
在项目中难免会用java处理json格式的数据，因此封装了一个JSONUtil工具类。 JSONUtil.java package com.bijian.json.study; import java.util.ArrayList; import java.util.Date; import java.util.HashMap;
[Zookeeper学习笔记之六]Zookeeper源代码分析之Zookeeper.WatchRegistration bit1129 zookeeper
Zookeeper类是Zookeeper提供给用户访问Zookeeper service的主要API，它包含了如下几个内部类首先分析它的内部类，从WatchRegistration开始，为指定的znode path注册一个Watcher， /** * Register a watcher for a particular p
【Scala十三】Scala核心七：部分应用函数 bit1129 scala
何为部分应用函数？ Partially applied function: A function that’s used in an expression and that misses some of its arguments.For instance, if function f has type Int => Int => Int, then f and f(1) are p
Tomcat Error listenerStart 终极大法 ronin47 tomcat
Tomcat报的错太含糊了，什么错都没报出来，只提示了Error listenerStart。为了调试，我们要获得更详细的日志。可以在WEB-INF/classes目录下新建一个文件叫logging.properties，内容如下 Java代码 handlers = org.apache.juli.FileHandler, java.util.logging.ConsoleHa
不用加减符号实现加减法 BrokenDreams 实现
今天有群友发了一个问题，要求不用加减符号(包括负号)来实现加减法。分析一下，先看最简单的情况，假设1+1，按二进制算的话结果是10，可以看到从右往左的第一位变为0，第二位由于进位变为1。
读《研磨设计模式》-代码笔记-状态模式-State bylijinnan java 设计模式
声明：本文只为方便我个人查阅和理解，详细的分析以及源代码请移步原作者的博客http://chjavach.iteye.com/ /* 当一个对象的内在状态改变时允许改变其行为，这个对象看起来像是改变了其类状态模式主要解决的是当控制一个对象状态的条件表达式过于复杂时的情况把状态的判断逻辑转移到表示不同状态的一系列类中，可以把复杂的判断逻辑简化如果在
CUDA程序block和thread超出硬件允许值时的异常 cherishLC CUDA
调用CUDA的核函数时指定block 和 thread大小，该大小可以是dim3类型的（三维数组），只用一维时可以是usigned int型的。以下程序验证了当block或thread大小超出硬件允许值时会产生异常！！！GPU根本不会执行运算！！！所以验证结果的正确性很重要！！！在VS中创建CUDA项目会有一个模板，里面有更详细的状态验证。以下程序在K5000GPU上跑的。
诡异的超长时间GC问题定位 chenchao051 jvm cms GC hbase swap
HBase的GC策略采用PawNew+CMS, 这是大众化的配置，ParNew经常会出现停顿时间特别长的情况，有时候甚至长到令人发指的地步，例如请看如下日志： 2012-10-17T05:54:54.293+0800: 739594.224: [GC 739606.508: [ParNew: 996800K->110720K(996800K), 178.8826900 secs] 3700
maven环境快速搭建 daizj 安装 mavne 环境配置
一下载maven 安装maven之前，要先安装jdk及配置JAVA_HOME环境变量。这个安装和配置java环境不用多说。 maven下载地址：http://maven.apache.org/download.html，目前最新的是这个apache-maven-3.2.5-bin.zip，然后解压在任意位置，最好地址中不要带中文字符，这个做java 的都知道，地址中出现中文会出现很多
PHP网站安全，避免PHP网站受到攻击的方法 dcj3sjt126com PHP
对于PHP网站安全主要存在这样几种攻击方式:1、命令注入(Command Injection)2、eval注入(Eval Injection)3、客户端脚本攻击(Script Insertion)4、跨网站脚本攻击(Cross Site Scripting, XSS)5、SQL注入攻击(SQL injection)6、跨网站请求伪造攻击(Cross Site Request Forgerie
yii中给CGridView设置默认的排序根据时间倒序的方法 dcj3sjt126com GridView
public function searchWithRelated() { $criteria = new CDbCriteria; $criteria->together = true; //without th
Java集合对象和数组对象的转换 dyy_gusi java集合
在开发中，我们经常需要将集合对象（List，Set）转换为数组对象，或者将数组对象转换为集合对象。Java提供了相互转换的工具，但是我们使用的时候需要注意，不能乱用滥用。 1、数组对象转换为集合对象最暴力的方式是new一个集合对象，然后遍历数组，依次将数组中的元素放入到新的集合中，但是这样做显然过
nginx同一主机部署多个应用 geeksun nginx
近日有一需求，需要在一台主机上用nginx部署2个php应用，分别是wordpress和wiki，探索了半天，终于部署好了，下面把过程记录下来。 1. 在nginx下创建vhosts目录，用以放置vhost文件。 mkdir vhosts 2. 修改nginx.conf的配置，在http节点增加下面内容设置，用来包含vhosts里的配置文件 #
ubuntu添加admin权限的用户账号 hongtoushizi ubuntu useradd
ubuntu创建账号的方式通常用到两种：useradd 和adduser . 本人尝试了useradd方法，步骤如下： 1:useradd 使用useradd时，如果后面不加任何参数的话，如：sudo useradd sysadm 创建出来的用户将是默认的三无用户：无home directory ,无密码,无系统shell。顾应该如下操作：
第五章常用Lua开发库2-JSON库、编码转换、字符串处理 jinnianshilongnian nginx lua
JSON库在进行数据传输时JSON格式目前应用广泛，因此从Lua对象与JSON字符串之间相互转换是一个非常常见的功能；目前Lua也有几个JSON库，本人用过cjson、dkjson。其中cjson的语法严格（比如unicode \u0020\u7eaf），要求符合规范否则会解析失败（如\u002），而dkjson相对宽松，当然也可以通过修改cjson的源码来完成
Spring定时器配置的两种实现方式OpenSymphony Quartz和java Timer详解 yaerfeng1989 timer quartz 定时器
原创整理不易，转载请注明出处：Spring定时器配置的两种实现方式OpenSymphony Quartz和java Timer详解代码下载地址：http://www.zuidaima.com/share/1772648445103104.htm 有两种流行Spring定时器配置：Java的Timer类和OpenSymphony的Quartz。 1.Java Timer定时首先继承jav
Linux下df与du两个命令的差别？ pda158 linux
　一、df显示文件系统的使用情况，与du比較，就是更全盘化。　　最经常使用的就是 df -T，显示文件系统的使用情况并显示文件系统的类型。　　举比例如以下：　　[root@localhost ~]# df -T 　　Filesystem Type &n
[转]SQLite的工具类 ---- 通过反射把Cursor封装到VO对象 ctfzh VO android sqlite 反射 Cursor
在写DAO层时，觉得从Cursor里一个一个的取出字段值再装到VO(值对象)里太麻烦了，就写了一个工具类，用到了反射，可以把查询记录的值装到对应的VO里，也可以生成该VO的List。使用时需要注意：考虑到Android的性能问题，VO没有使用Setter和Getter，而是直接用public的属性。表中的字段名需要和VO的属性名一样，要是不一样就得在查询的SQL中
该学习笔记用到的Employee表 vipbooks oracle sql 工作
这是我在学习Oracle是用到的Employee表，在该笔记中用到的就是这张表，大家可以用它来学习和练习。 drop table Employee; -- 员工信息表 create table Employee( -- 员工编号 EmpNo number(3) primary key, -- 姓

	F1	F2	F3	F4	target
0	5.1	3.5	1.4	0.2	0.0
1	4.9	3.0	1.4	0.2	0.0
2	4.7	3.2	1.3	0.2	0.0
3	4.6	3.1	1.5	0.2	0.0
4	5.0	3.6	1.4	0.2	0.0
...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	2.0
146	6.3	2.5	5.0	1.9	2.0
147	6.5	3.0	5.2	2.0	2.0
148	6.2	3.4	5.4	2.3	2.0
149	5.9	3.0	5.1	1.8	2.0

	ones	F1	F2	F3	F4	target
0	1	5.1	3.5	1.4	0.2	0.0
1	1	4.9	3.0	1.4	0.2	0.0
2	1	4.7	3.2	1.3	0.2	0.0
3	1	4.6	3.1	1.5	0.2	0.0
4	1	5.0	3.6	1.4	0.2	0.0
...	...	...	...	...	...	...
145	1	6.7	3.0	5.2	2.3	2.0
146	1	6.3	2.5	5.0	1.9	2.0
147	1	6.5	3.0	5.2	2.0	2.0
148	1	6.2	3.4	5.4	2.3	2.0
149	1	5.9	3.0	5.1	1.8	2.0

	ones	F1	F2	F3	F4	target
0	1	5.1	3.5	1.4	0.2	0
1	1	4.9	3.0	1.4	0.2	0
2	1	4.7	3.2	1.3	0.2	0
3	1	4.6	3.1	1.5	0.2	0
4	1	5.0	3.6	1.4	0.2	0
...	...	...	...	...	...	...
145	1	6.7	3.0	5.2	2.3	2
146	1	6.3	2.5	5.0	1.9	2
147	1	6.5	3.0	5.2	2.0	2
148	1	6.2	3.4	5.4	2.3	2
149	1	5.9	3.0	5.1	1.8	2

	ones	F1	F2	F3	F4	target
0	1	5.1	3.5	1.4	0.2	0
1	1	4.9	3.0	1.4	0.2	0
2	1	4.7	3.2	1.3	0.2	0
3	1	4.6	3.1	1.5	0.2	0
4	1	5.0	3.6	1.4	0.2	0
...	...	...	...	...	...	...
145	1	6.7	3.0	5.2	2.3	2
146	1	6.3	2.5	5.0	1.9	2
147	1	6.5	3.0	5.2	2.0	2
148	1	6.2	3.4	5.4	2.3	2
149	1	5.9	3.0	5.1	1.8	2

	ones	F1	F2	F3	F4	target
0	1	5.1	3.5	1.4	0.2	1
1	1	4.9	3.0	1.4	0.2	1
2	1	4.7	3.2	1.3	0.2	1
3	1	4.6	3.1	1.5	0.2	1
4	1	5.0	3.6	1.4	0.2	1
...	...	...	...	...	...	...
145	1	6.7	3.0	5.2	2.3	0
146	1	6.3	2.5	5.0	1.9	0
147	1	6.5	3.0	5.2	2.0	0
148	1	6.2	3.4	5.4	2.3	0
149	1	5.9	3.0	5.1	1.8	0

	ones	F1	F2	F3	F4	target
50	1	7.0	3.2	4.7	1.4	1
51	1	6.4	3.2	4.5	1.5	1
52	1	6.9	3.1	4.9	1.5	1
53	1	5.5	2.3	4.0	1.3	1
54	1	6.5	2.8	4.6	1.5	1

	ones	F1	F2	F3	F4	target
0	1	5.1	3.5	1.4	0.2	0
1	1	4.9	3.0	1.4	0.2	0
2	1	4.7	3.2	1.3	0.2	0
3	1	4.6	3.1	1.5	0.2	0
4	1	5.0	3.6	1.4	0.2	0
...	...	...	...	...	...	...
145	1	6.7	3.0	5.2	2.3	1
146	1	6.3	2.5	5.0	1.9	1
147	1	6.5	3.0	5.2	2.0	1
148	1	6.2	3.4	5.4	2.3	1
149	1	5.9	3.0	5.1	1.8	1

	模型1	模糊2	模型3
0	1	0	0
1	1	0	0
2	1	0	0
3	1	0	0
4	1	0	0
...	...	...	...
145	0	0	1
146	0	1	1
147	0	0	1
148	0	0	1
149	0	0	1

	F1	F2	F3	F4	target
0	5.1	3.5	1.4	0.2	0.0
1	4.9	3.0	1.4	0.2	0.0
2	4.7	3.2	1.3	0.2	0.0
3	4.6	3.1	1.5	0.2	0.0
4	5.0	3.6	1.4	0.2	0.0
...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	2.0
146	6.3	2.5	5.0	1.9	2.0
147	6.5	3.0	5.2	2.0	2.0
148	6.2	3.4	5.4	2.3	2.0
149	5.9	3.0	5.1	1.8	2.0

	ones	F1	F2	F3	F4	target
0	1	5.1	3.5	1.4	0.2	0.0
1	1	4.9	3.0	1.4	0.2	0.0
2	1	4.7	3.2	1.3	0.2	0.0
3	1	4.6	3.1	1.5	0.2	0.0
4	1	5.0	3.6	1.4	0.2	0.0
...	...	...	...	...	...	...
145	1	6.7	3.0	5.2	2.3	2.0
146	1	6.3	2.5	5.0	1.9	2.0
147	1	6.5	3.0	5.2	2.0	2.0
148	1	6.2	3.4	5.4	2.3	2.0
149	1	5.9	3.0	5.1	1.8	2.0

	ones	F1	F2	F3	F4	target
0	1	5.1	3.5	1.4	0.2	0
1	1	4.9	3.0	1.4	0.2	0
2	1	4.7	3.2	1.3	0.2	0
3	1	4.6	3.1	1.5	0.2	0
4	1	5.0	3.6	1.4	0.2	0
...	...	...	...	...	...	...
145	1	6.7	3.0	5.2	2.3	2
146	1	6.3	2.5	5.0	1.9	2
147	1	6.5	3.0	5.2	2.0	2
148	1	6.2	3.4	5.4	2.3	2
149	1	5.9	3.0	5.1	1.8	2

	ones	F1	F2	F3	F4	target
0	1	5.1	3.5	1.4	0.2	0
1	1	4.9	3.0	1.4	0.2	0
2	1	4.7	3.2	1.3	0.2	0
3	1	4.6	3.1	1.5	0.2	0
4	1	5.0	3.6	1.4	0.2	0
...	...	...	...	...	...	...
145	1	6.7	3.0	5.2	2.3	2
146	1	6.3	2.5	5.0	1.9	2
147	1	6.5	3.0	5.2	2.0	2
148	1	6.2	3.4	5.4	2.3	2
149	1	5.9	3.0	5.1	1.8	2

	ones	F1	F2	F3	F4	target
0	1	5.1	3.5	1.4	0.2	1
1	1	4.9	3.0	1.4	0.2	1
2	1	4.7	3.2	1.3	0.2	1
3	1	4.6	3.1	1.5	0.2	1
4	1	5.0	3.6	1.4	0.2	1
...	...	...	...	...	...	...
145	1	6.7	3.0	5.2	2.3	0
146	1	6.3	2.5	5.0	1.9	0
147	1	6.5	3.0	5.2	2.0	0
148	1	6.2	3.4	5.4	2.3	0
149	1	5.9	3.0	5.1	1.8	0

	ones	F1	F2	F3	F4	target
50	1	7.0	3.2	4.7	1.4	1
51	1	6.4	3.2	4.5	1.5	1
52	1	6.9	3.1	4.9	1.5	1
53	1	5.5	2.3	4.0	1.3	1
54	1	6.5	2.8	4.6	1.5	1

	ones	F1	F2	F3	F4	target
0	1	5.1	3.5	1.4	0.2	0
1	1	4.9	3.0	1.4	0.2	0
2	1	4.7	3.2	1.3	0.2	0
3	1	4.6	3.1	1.5	0.2	0
4	1	5.0	3.6	1.4	0.2	0
...	...	...	...	...	...	...
145	1	6.7	3.0	5.2	2.3	1
146	1	6.3	2.5	5.0	1.9	1
147	1	6.5	3.0	5.2	2.0	1
148	1	6.2	3.4	5.4	2.3	1
149	1	5.9	3.0	5.1	1.8	1

	模型1	模糊2	模型3
0	1	0	0
1	1	0	0
2	1	0	0
3	1	0	0
4	1	0	0
...	...	...	...
145	0	0	1
146	0	1	1
147	0	0	1
148	0	0	1
149	0	0	1

【Python机器学习】实验04(1) 多分类(基于逻辑回归)实践

文章目录

多分类以及机器学习实践

如何对多个类别进行分类

1.1 数据的预处理

1.2 训练数据的准备

1.3 定义假设函数，代价函数，梯度下降算法（从实验3复制过来）

1.4 调用梯度下降算法来学习三个分类模型的参数

1.5 利用模型进行预测

1.6 评估模型

1.7 试试sklearn

实验4(1) 请动手完成你们第一个多分类问题，祝好运！完成下面代码

2.1 数据读取

2.2 训练数据的准备

2.3 定义假设函数、代价函数和梯度下降算法

2.4 学习这四个分类模型

2.5 利用模型进行预测

2.6 计算准确率

你可能感兴趣的:(《,Python机器学习入门实验,》,机器学习,python,分类)

	F1	F2	F3	F4	target
0	5.1	3.5	1.4	0.2	0.0
1	4.9	3.0	1.4	0.2	0.0
2	4.7	3.2	1.3	0.2	0.0
3	4.6	3.1	1.5	0.2	0.0
4	5.0	3.6	1.4	0.2	0.0
...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	2.0
146	6.3	2.5	5.0	1.9	2.0
147	6.5	3.0	5.2	2.0	2.0
148	6.2	3.4	5.4	2.3	2.0
149	5.9	3.0	5.1	1.8	2.0

	ones	F1	F2	F3	F4	target
0	1	5.1	3.5	1.4	0.2	0.0
1	1	4.9	3.0	1.4	0.2	0.0
2	1	4.7	3.2	1.3	0.2	0.0
3	1	4.6	3.1	1.5	0.2	0.0
4	1	5.0	3.6	1.4	0.2	0.0
...	...	...	...	...	...	...
145	1	6.7	3.0	5.2	2.3	2.0
146	1	6.3	2.5	5.0	1.9	2.0
147	1	6.5	3.0	5.2	2.0	2.0
148	1	6.2	3.4	5.4	2.3	2.0
149	1	5.9	3.0	5.1	1.8	2.0

	ones	F1	F2	F3	F4	target
0	1	5.1	3.5	1.4	0.2	0
1	1	4.9	3.0	1.4	0.2	0
2	1	4.7	3.2	1.3	0.2	0
3	1	4.6	3.1	1.5	0.2	0
4	1	5.0	3.6	1.4	0.2	0
...	...	...	...	...	...	...
145	1	6.7	3.0	5.2	2.3	2
146	1	6.3	2.5	5.0	1.9	2
147	1	6.5	3.0	5.2	2.0	2
148	1	6.2	3.4	5.4	2.3	2
149	1	5.9	3.0	5.1	1.8	2

	ones	F1	F2	F3	F4	target
0	1	5.1	3.5	1.4	0.2	0
1	1	4.9	3.0	1.4	0.2	0
2	1	4.7	3.2	1.3	0.2	0
3	1	4.6	3.1	1.5	0.2	0
4	1	5.0	3.6	1.4	0.2	0
...	...	...	...	...	...	...
145	1	6.7	3.0	5.2	2.3	2
146	1	6.3	2.5	5.0	1.9	2
147	1	6.5	3.0	5.2	2.0	2
148	1	6.2	3.4	5.4	2.3	2
149	1	5.9	3.0	5.1	1.8	2

	ones	F1	F2	F3	F4	target
0	1	5.1	3.5	1.4	0.2	1
1	1	4.9	3.0	1.4	0.2	1
2	1	4.7	3.2	1.3	0.2	1
3	1	4.6	3.1	1.5	0.2	1
4	1	5.0	3.6	1.4	0.2	1
...	...	...	...	...	...	...
145	1	6.7	3.0	5.2	2.3	0
146	1	6.3	2.5	5.0	1.9	0
147	1	6.5	3.0	5.2	2.0	0
148	1	6.2	3.4	5.4	2.3	0
149	1	5.9	3.0	5.1	1.8	0

	ones	F1	F2	F3	F4	target
50	1	7.0	3.2	4.7	1.4	1
51	1	6.4	3.2	4.5	1.5	1
52	1	6.9	3.1	4.9	1.5	1
53	1	5.5	2.3	4.0	1.3	1
54	1	6.5	2.8	4.6	1.5	1

	ones	F1	F2	F3	F4	target
0	1	5.1	3.5	1.4	0.2	0
1	1	4.9	3.0	1.4	0.2	0
2	1	4.7	3.2	1.3	0.2	0
3	1	4.6	3.1	1.5	0.2	0
4	1	5.0	3.6	1.4	0.2	0
...	...	...	...	...	...	...
145	1	6.7	3.0	5.2	2.3	1
146	1	6.3	2.5	5.0	1.9	1
147	1	6.5	3.0	5.2	2.0	1
148	1	6.2	3.4	5.4	2.3	1
149	1	5.9	3.0	5.1	1.8	1

	模型1	模糊2	模型3
0	1	0	0
1	1	0	0
2	1	0	0
3	1	0	0
4	1	0	0
...	...	...	...
145	0	0	1
146	0	1	1
147	0	0	1
148	0	0	1
149	0	0	1