动手学深度学习——实战Kaggle比赛：预测房价（代码详解+调参优化）

1. 下载和缓存数据集

数据集百度云：
链接：https://pan.baidu.com/s/14CVZBjmlKA_c3MYNFLSvbg?pwd=pysi 提取码：pysi
1、导入包

# 导入所需要的包
import hashlib
import os
import tarfile
import zipfile
import requests

#@save
# DATA_HUB为二元组：包含数据集的url和验证文件完整性的sha-1密钥
DATA_HUB = dict()

# 数据集托管在DATA_URL的站点上
DATA_URL = 'http://d2l-data.s3-accelerate.amazonaws.com/'

2、下载数据集并保存数据集

• os.makedirs(cache_dir, exist_ok=True)：创建目录，exist_ok = True指定了，如果某个要创建的目录已经存在，也不报错。
• shal.sha1()：创建一个字符串hashlib_，并将其加密后传入。
• os.path.join()：连接两个或更多的路径名组件
  1.如果各组件名首字母不包含’/’，则函数会自动加上
  2.如果有一个组件是一个绝对路径，则在它之前的所有组件均会被舍弃
  3.如果最后一个组件为空，则生成的路径以一个’/’分隔符结尾

"""
    定义download函数：
    1、下载数据集，将数据集缓存在本地目录（../data），并返回下载文件的名称
    2、如果缓存目录中存在此数据集文件，并且与sha-1与存储在DATA_HUB中相匹配，则使用缓存的文件
"""
# download(文件名称，缓存目录)
def download(name, cache_dir=os.path.join('..', 'data')): #@save
    """下载一个DATA_HUB中的文件，返回本地文件名"""
    # 判断数据集是否存在于DATA_HUB
    assert name in DATA_HUB, f"{name} 不存在于 {DATA_HUB}"
    url, sha1_hash = DATA_HUB[name]
    
    # 创建缓存目录
    os.makedirs(cache_dir, exist_ok=True)
    
    # 进行路径拼接，最后以'/'分隔符结尾
    fname = os.path.join(cache_dir, url.split('/')[-1])
    
    # 判断是否存在缓存文件
    if os.path.exists(fname):
        sha1 = hashlib.sha1()
        with open(fname, 'rb') as f:
            while True:
                data = f.read(1048576)
                if not data:
                    break
                sha1.update(data)
        if sha1.hexdigest() == sha1_hash:
            return fname # 命中缓存
    print(f'正在从{url}下载{fname}...')
    r = requests.get(url, stream=True, verify=True)
    
    # 将文件进行保存
    with open(fname, 'wb') as f:
        f.write(r.content)
    return fname

3、将下载的数据集进行解压操作

"""
    实现两个实用函数：
    1、一个将下载并解压缩一个zip/tar文件
    2、将使用的数据集从DATA_HUB下载到缓存目录
"""
def download_extract(name, folder=None): #@save
    """下载并解压zip/tar文件"""
    fname = dowanload(name)
    base_dir = os.path.dirname(fname)
    data_dir = os.path.splitext(fname)
    
    # 只对zip/tar/gz格式的压缩文件进行解压
    if ext == '.zip':
        fp = zipfile.Zipfile(fname, 'r')
    elif ext in ('.tar', '.gz'):
        fp = tarfile.open(fname, 'r')
    else:
        assert False, '只有zip/tar文件可以解压'
    fp.extractall(base_dir)
    return os.path.join(base_dir, folder) if folder else data_dir

def download_all(): #@save
    """下载DATA_HUB中的所有文件"""
    for name in DATA_HUB:
        download(name)

2. Kaggle

Kaggle是一个当今流行举办机器学习比赛的平台，这里是房价预测比赛页面https://www.kaggle.com/c/house-prices-advanced-regression-techniques。

3. 访问和读取数据集

1、安装并导入pandas等包

# 如果没有安装pandas，请取消下一行的注释
# !pip install pandas

%matplotlib inline
import numpy as np
import pandas as pd
import torch
from torch import nn
from d2l import torch as d2l

2、使用定义的脚本下载并缓存Kaggle房屋数据集

# 使用上面定义的脚本下载并缓存Kaggle房屋数据集
DATA_HUB['kaggle_house_train'] = (  #@save
    DATA_URL + 'kaggle_house_pred_train.csv',
    '585e9cc93e70b39160e7921475f9bcd7d31219ce')

DATA_HUB['kaggle_house_test'] = (  #@save
    DATA_URL + 'kaggle_house_pred_test.csv',
    'fa19780a7b011d9b009e8bff8e99922a8ee2eb90')

# 使用pandas分布加载包含训练数据和测试数据的两个csv文件
train_data = pd.read_csv(download('kaggle_house_train'))
test_data = pd.read_csv(download('kaggle_house_test'))

这里查看一下样本特征

# 训练数据集包括1460个样本，每个样本80个特征和1个标签
# 测试数据集包括1459个样本，每个样本80个特征
print(train_data.shape)
print(test_data.shape)

# 前四个和最后两个特征，以及相应标签（房价）
print(train_data.iloc[0:4, [0, 1, 2, 3, -3, -2, -1]])

3、对于每个样本：删除第一个特征ID，因为其不携带任何用于预测的信息

# 对于每个样本：删除第一个特征ID，因为其不携带任何用于预测的信息
all_features = pd.concat((train_data.iloc[:, 1:-1], test_data.iloc[:, 1:-1]))

4. 数据预处理

1、对数据进行标准化处理

"""
    数据预处理：
    1、将所有缺失的值替换为相应特征的平均值
    2、为了将所有数据放在共同的尺度上，通过特征重新缩放到零均值和单位方差来标准化数据
        （1）方便优化
        （2）不知道哪些特征是相关的，所以不想让惩罚分配给一个特征的系数比分配给其他特征的系数更大
    3、处理离散值，用独热编码来替换。如"MSZoning_RL"为1，"MSZoning_RM"为0
"""
# 若无法获得测试数据，则可根据训练数据计算均值和标准差：x←(x-μ)/σ
# 获取无法获得测试数据的数量
numeric_features = all_features.dtypes[all_features.dtypes != 'object'].index
all_features[numeric_features] = all_features[numeric_features].apply(
    lambda x: (x - x.mean()) / (x.std())) 
# 在标准化数据之后，所有均值消失，因此我们可以将缺失值设置为0
all_features[numeric_features] = all_features[numeric_features].fillna(0)

2、将缺失值进行替换

#“Dummy_na=True”将“na”（缺失值）视为有效的特征值，并为其创建指示符特征
# all_features是删除ID那一列之后，将每个样本中所有的特征连接起来
all_features = pd.get_dummies(all_features, dummy_na=True)
all_features.shape

3、通过values属性，我们可以 从pandas格式中提取NumPy格式，并将其转换为张量表示用于训练。

# 通过values属性将数据从pandas格式提取numpy格式，并将其转为张量用于训练
n_train = train_data.shape[0]
train_features = torch.tensor(all_features[:n_train].values, dtype=torch.float32)
test_features = torch.tensor(all_features[n_train:].values, dtype=torch.float32)

# 获取训练集的价格标签，将其转换为张量
train_labels = torch.tensor(
    train_data.SalePrice.values.reshape(-1, 1), dtype=torch.float32)

5. 训练

1、定义损失函数和模型

"""
    训练一个带有损失平方的线性模型：
    1、损失函数为损失平方
    2、线性模型作为基线模型
"""
loss = nn.MSELoss()
in_features = train_features.shape[1]

def get_net():
    net = nn.Sequential(nn.Linear(in_features,1))
    return net

2、采用价格预测的对数来衡量差异

• clamp（）：功能将输入input张量每个元素的值压缩到区间 [min,max]，并返回结果到一个新张量。

# 采用价格预测的对数来衡量差异：√￣(1/n*(∑(logy - logy')^2))
def log_rmse(net, features, labels):
    # 为了在取对数时进一步稳定该值，将小于1的值设置为1
    clipped_preds = torch.clamp(net(features), 1, float('inf'))
    rmse = torch.sqrt(loss(torch.log(clipped_preds),
                          torch.log(labels)))
    return rmse.item()

3、进行训练，优化器借助Adam优化器

• append：python中的一个函数，它主要是用来在列表末尾添加新的对象。

# 优化器借助Adam优化器
"""
    定义训练函数：
    1、加载训练数据集
    2、使用Adam优化器（对初始学习率不那么敏感）
    3、进行训练：计算损失，进行梯度优化，返回训练损失和测试损失
"""
def train(net, train_features, train_labels, test_features, test_labels,
         num_epochs, learning_rate, weight_decay, batch_size):
    train_ls, test_ls = [], []
    train_iter = d2l.load_array((train_features, train_labels), batch_size)
    # 这里使用的是Adam优化算法
    optimizer = torch.optim.Adam(net.parameters(),
                                lr = learning_rate,
                                weight_decay = weight_decay)
    for epoch in range(num_epochs):
        for X,y in train_iter:
            optimizer.zero_grad() # 梯度归零
            l = loss(net(X), y) # 计算损失
            l.backward() # 更新梯度
            optimizer.step()
            
        # 将训练损失加到训练损失列表中
        train_ls.append(log_rmse(net, train_features, train_labels))
        
        # 如果测试标签不为空，将测试损失加到测试损失列表中
        if test_labels is not None:
            test_ls.append(log_rmse(net, test_features, test_labels))
    return train_ls,  test_ls

6. K折交叉验证

1、定义K折交叉验证

• cat() 函数： 在给定维度上对输入的张量序列seq 进行连接操作。

"""
    定义K折交叉验证:
    1、当k > 1时，进行K折交叉验证，将数据集分为K份
    2、选择第i个切片作为验证集，其余部分作为训练数据
    3、第一片的训练数据直接填进去，之后的使用cat进行相连接
""" 
def get_k_fold_data(k, i, X, y):
    # 假设k折大于1，将数据集分成k份
    assert k > 1
    fold_size = X.shape[0] // k 
    X_train, y_train = None, None
    for j in range(k):
        idx = slice(j * fold_size, (j + 1) * fold_size)
        X_part, y_part = X[idx, :], y[idx]
        
        # 将第i片数据集作为验证集
        if j == i:
            X_valid, y_valid = X_part, y_part
            
        # 其他余下的片作为训练集
        elif X_train is None:
            X_train, y_train = X_part, y_part
            
        # 使用cat()函数将余下的训练集片进行拼接
        else:
            X_train = torch.cat([X_train, X_part], 0) 
            y_train = torch.cat([y_train, y_part], 0)
    return X_train, y_train, X_valid, y_valid

2、在K折交叉验证中训练K次

"""
    在K折交叉验证中训练K次：
    1、返回训练和验证误差的平均值
    2、可视化训练误差和验证误差
"""
def k_fold(k, X_train, y_train, num_epochs, learning_rate, weight_decay,
          batch_size):
    train_l_sum, valid_l_sum = 0, 0
    for i in range(k):
        # 进行k折交叉验证
        data = get_k_fold_data(k, i, X_train, y_train)
        net = get_net()
        train_ls, valid_ls = train(net, *data, num_epochs, learning_rate,
                                  weight_decay, batch_size)
        train_l_sum += train_ls[-1]
        valid_l_sum += valid_ls[-1]
        if i == 0:
            # 画图：训练损失和验证损失
            d2l.plot(list(range(1, num_epochs + 1)), [train_ls, valid_ls],
                     xlabel='epoch', ylabel='rmse', xlim=[1, num_epochs],
                     legend=['train', 'valid'], yscale='log')
        print(f'折{i + 1}, 训练log rmse{float(train_ls[-1]):f},'
             f'验证log rmse{float(valid_ls[-1]):f}')
    return train_l_sum / k, valid_l_sum / k

7. 模型选择

1、选择一组未调优的超参数。
k折：5，迭代轮数：100，学习率：5，权重：0，批量大小：64

# 模型选择
k, num_epochs, lr, weight_decay, batch_size = 5, 100, 5, 0, 64
train_l, valid_l = k_fold(k, train_features, train_labels, num_epochs, lr, weight_decay,
          batch_size)
print(f'{k}-折验证：平均训练log rmse：{float(train_l):f},'
     f'平均验证log rmse：{float(valid_l):f}')

8. 提交Kaggle预测

"""
    提交Kaggle预测：
    1、使用所有数据进行训练，得到模型
    2、该模型可以应用到测试集上，将预测保存在csv文件
"""
def train_and_pred(train_features, test_features, train_labels, test_data,
                  num_epochs, lr, weight_decay, batch_size):
    net = get_net()
    train_ls, _ = train(net, train_features, train_labels, None, None,
         num_epochs, lr, weight_decay, batch_size)
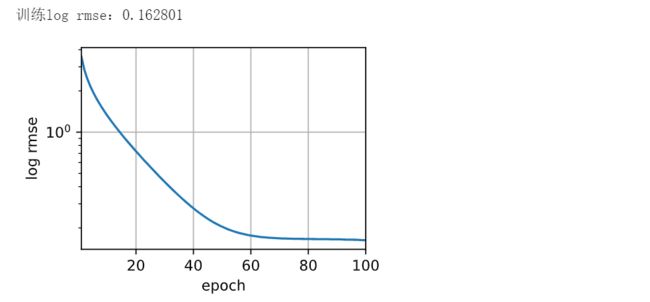
    d2l.plot(np.arange(1, num_epochs + 1), [train_ls], xlabel='epoch',
            ylabel='log rmse', xlim=[1, num_epochs], yscale='log')
    print(f'训练log rmse：{float(train_ls[-1]):f}')
    # 将网络应用与测试集。
    preds = net(test_features).detach().numpy()
    # 将其重新格式化以导出到Kaggle
    test_data['SalePrice'] = pd.Series(preds.reshape(1, -1)[0])
    submission = pd.concat([test_data['Id'], test_data['SalePrice']], axis=1)
    submission.to_csv('submission.csv', index=False)

train_and_pred(train_features, test_features, train_labels, test_data,
                  num_epochs, lr, weight_decay, batch_size)

9. 调参优化

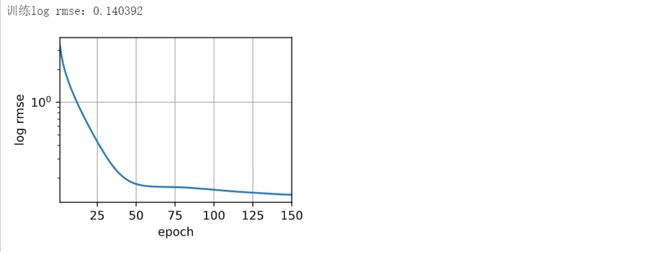
因为之前是给的未优化的超参数，我们可以对k, num_epochs, lr, weight_decay, batch_size进行调参优化，这里给出一组超参数：

k, num_epochs, lr, weight_decay, batch_size = 8, 150, 6, 0, 64

其他的超参数可以试一下

组别\超参数	k	num_epochs	lr	weight_decay	batch_size	训练损失	验证损失	测试损失
原始	5	100	5	0	64	0.1653	0.1705	0.1628
第一组	5	100	8	0	64	0.1539	0.1630	0.1460
第二组	6	100	8	0	64	0.1534	0.1609	0.1460
第三组	8	100	8	0	64	0.1512	0.1593	0.1460
第五组	12	100	8	0	64	0.1488	0.1553	0.1456
第六组	20	100	8	0	64	0.1475	0.1543	0.1457
第七组	8	150	6	0	64	0.1447	0.1537	0.1404
第八组	12	200	8	0	64	0.1299	0.1432	0.1288
第九组	20	300	8	0	64	0.1248	0.1470	0.1247
第十组	8	100	8	0	32	0.1331	0.1450	0.1308
第十一组	12	200	8	0	32	0.1240	0.1470	0.1243

这里只是针对线性模型的部分参数优化