3527: [Zjoi2014]力

题目大意：给出n个数qi，定义 Fj为

      

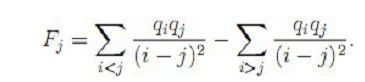
 令 Ei=Fi/qi，求Ei。

设A[i]=q[i],B[i]=1/(i^2)。

设C[i]=sigma(A[j]*B[i-j]),D[i]=sigma(A[n-j-1]*B[i-j])。

那么所求的E[i]=C[i]-D[i]。

不难发现C[i]已经是标准的卷积形式了，用FFT即可。

对于D[i],令A'[i]=A[n-i-1]，那么D[i]=sigma(A[j]*B[i-j])，于是也用FFT即可。

code:

 1 #include<cstdio> 

 2 #include<iostream> 

 3 #include<cmath> 

 4 #include<cstring> 

 5 #include<algorithm> 

 6 #define maxn 262144 

 7 #define pi 3.14159265358979323846 

 8 using namespace std; 

 9 char ch; 

10 int m,n; 

11 bool ok; 

12 long double ans[maxn]; 

13 double q[maxn]; 

14 void read(int &x){ 

15     for (ok=0,ch=getchar();!isdigit(ch);ch=getchar()) if (ch=='-') ok=1; 

16     for (x=0;isdigit(ch);x=x*10+ch-'0',ch=getchar()); 

17     if (ok) x=-x; 

18 } 

19 struct comp{ 

20     long double rea,ima; 

21     void clear(){rea=ima=0;} 

22     comp operator +(const comp &x){return (comp){rea+x.rea,ima+x.ima};} 

23     comp operator -(const comp &x){return (comp){rea-x.rea,ima-x.ima};} 

24     comp operator *(const comp &x){return (comp){rea*x.rea-ima*x.ima,rea*x.ima+ima*x.rea};} 

25 }a[maxn],b[maxn],c[maxn],tmp[maxn],w,wn; 

26 void fft(comp *a,int st,int siz,int step,int op){ 

27     if (siz==1) return; 

28     fft(a,st,siz>>1,step<<1,op),fft(a,st+step,siz>>1,step<<1,op); 

29     int x=st,x1=st,x2=st+step; 

30     w=(comp){1,0},wn=(comp){cos(op*2*pi/siz),sin(op*2*pi/siz)}; 

31     for (int i=0;i<(siz>>1);i++,x+=step,x1+=(step<<1),x2+=(step<<1),w=w*wn) 

32         tmp[x]=a[x1]+(w*a[x2]),tmp[x+(siz>>1)*step]=a[x1]-(w*a[x2]); 

33     for (int i=st;siz;i+=step,siz--) a[i]=tmp[i]; 

34 } 

35 int main(){ 

36     read(m),n=1; 

37     while (n<(m<<1)) n<<=1; 

38     for (int i=0;i<m;i++) scanf("%lf",&q[i]); 

39       

40     for (int i=0;i<n;i++) a[i].clear(); 

41     for (int i=0;i<n;i++) b[i].clear(); 

42     for (int i=0;i<m;i++) a[i].rea=q[i]; 

43     for (int i=1;i<m;i++) b[i].rea=1.0/i/i; 

44     fft(a,0,n,1,1),fft(b,0,n,1,1); 

45     for (int i=0;i<n;i++) c[i]=a[i]*b[i]; 

46     fft(c,0,n,1,-1); 

47     for (int i=0;i<m;i++) ans[i]=c[i].rea/n; 

48       

49     for (int i=0;i<n;i++) a[i].clear(); 

50     for (int i=0;i<n;i++) b[i].clear(); 

51     for (int i=0;i<m;i++) a[i].rea=q[m-i-1]; 

52     for (int i=1;i<m;i++) b[i].rea=1.0/i/i; 

53     fft(a,0,n,1,1),fft(b,0,n,1,1); 

54     for (int i=0;i<n;i++) c[i]=a[i]*b[i]; 

55     fft(c,0,n,1,-1); 

56       

57     for (int i=0;i<m;i++) printf("%.9lf\n",(double)(ans[i]-c[m-i-1].rea/n)); 

58     return 0; 

59 }