文章目录
- 一、入门
-
- 二、中等
-
- 1. 序列问题
-
- 2. 两个维度权衡问题
-
- 3. 股票问题
- 三、进阶
-
- T53. 最大子数组和(dp或者贪心)
- T134. 加油站
- T968. 监控二叉树
- 0. 区间问题
-
- T55. 跳跃游戏 (能否到达)
- T45. 跳跃游戏Ⅱ ****
- T452. 用最少数量的箭引爆气球
- T435. 无重叠区间
- T763. 划分字母区间
- T56. 合并区间

一、入门
T455. 分发饼干

class Solution {
public int findContentChildren(int[] g, int[] s) {
Arrays.sort(g);
Arrays.sort(s);
int count = 0;
int start = 0;
for(int i = 0;i<s.length&&start<g.length;i++){
if(s[i]>=g[start]){
start++;
count++;
}
}
return count;
}
}
二、中等
1. 序列问题
376. 摆动序列

class Solution {
public int wiggleMaxLength(int[] nums) {
if (nums.length == 1){return 1;}
int pre = 0;
int cur = 0;
int count = 1;
for(int i = 1;i<nums.length;i++){
cur = nums[i] - nums[i-1];
if ((cur>0&&pre<=0)|| (cur<0&&pre>=0)){
count++;
pre = cur;
}
}
return count;
}
}
2. 两个维度权衡问题
T406. 根据身高重建队列
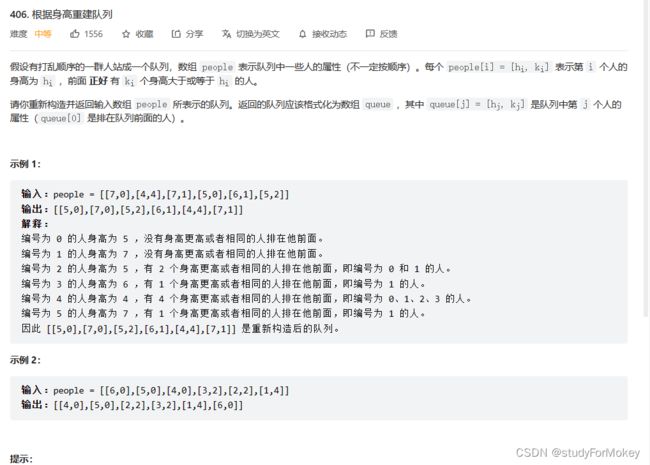
class Solution {
public int[][] reconstructQueue(int[][] people) {
Arrays.sort(people,(x,y)->{
if(x[0] == y[0]){return x[1] - y[1];}
return y[0] - x[0];
});
LinkedList<int[]> que = new LinkedList<>();
for(int[] p:people){
que.add(p[1],p);
}
return que.toArray(new int[people.length][2]);
}
}
3. 股票问题
三、进阶
T53. 最大子数组和(dp或者贪心)

class Solution {
public int maxSubArray(int[] nums) {
if(nums.length == 1){return nums[0];}
int sum = Integer.MIN_VALUE;
int count = 0;
for(int i = 0;i<nums.length;i++){
count = count + nums[i];
sum = Math.max(count,sum);
if(count<0){
count=0;
}
}
return sum;
}
}
T134. 加油站

- 思路分析
总的耗油量必须大于0;
如果出现求和小于0,那么必然不是起点
class Solution {
public int canCompleteCircuit(int[] gas, int[] cost) {
int rest = 0;
int sum = 0;
int index = 0;
for(int i = 0;i<gas.length;i++){
rest += gas[i] - cost[i];
sum += gas[i] - cost[i];
if(rest<0){
rest = 0;
index = i + 1;
}
}
if(sum<0){return -1;}
return index;
}
}
T968. 监控二叉树

- 思路分析
从下往上看,局部最优:让叶子节点的父节点安摄像头,所用摄像头最少,整体最优:全部摄像头数量所用最少!
每个节点可能有3种状态:
该节点无覆盖
本节点有摄像头
本节点有覆盖
- 代码实现
class Solution {
int sum = 0;
public int minCameraCover(TreeNode root) {
if(root == null){return 0;}
if(minHelper(root) == 2){sum++;}
return sum;
}
public int minHelper(TreeNode root){
if(root == null){
return 1;
}
int left = minHelper(root.left);
int right = minHelper(root.right);
if (left == 2 || right == 2){
sum++;
return 0;
}else if(left == 1 && right == 1){
return 2;
}else{
return 1;
}
}
}
0. 区间问题
T55. 跳跃游戏 (能否到达)

class Solution {
public boolean canJump(int[] nums) {
if(nums.length == 1){return true;}
int cover = 0;
for(int i = 0;i<=cover;i++){
cover = Math.max(cover,i+nums[i]);
if(cover>=nums.length-1){
return true;
}
}
return false;
}
}
T45. 跳跃游戏Ⅱ ****

- 思路分析
如果某一个作为 起跳点 的格子可以跳跃的距离是 3,那么表示后面 3 个格子都可以作为 起跳点。
- 可以对每一个能作为 起跳点 的格子都尝试跳一次,把 能跳到最远的距离 不断更新。
如果从这个 起跳点 起跳叫做第 1 次 跳跃,那么从后面 3 个格子起跳 都 可以叫做第 2 次 跳跃。
所以,当一次 跳跃 结束时,从下一个格子开始,到现在 能跳到最远的距离,都 是下一次 跳跃 的 起跳点。
- 对每一次 跳跃 用 for 循环来模拟。
- 跳完一次之后,更新下一次 起跳点 的范围。
- 在新的范围内跳,更新 能跳到最远的距离。
记录 跳跃 次数,如果跳到了终点,就得到了结果。

- 代码实现
class Solution {
public int jump(int[] nums) {
if(nums.length == 1) return 0;
int start = 0;
int cover = nums[0];
int step = 1;
while(cover < nums.length-1){
int tempStart = start;
int tempEnd = cover;
for(int i=tempStart;i<=tempEnd;i++){
if(i+nums[i]>cover){
cover = i+nums[i];
start = i + 1;
}
}
step++;
}
return step;
}
}
T452. 用最少数量的箭引爆气球
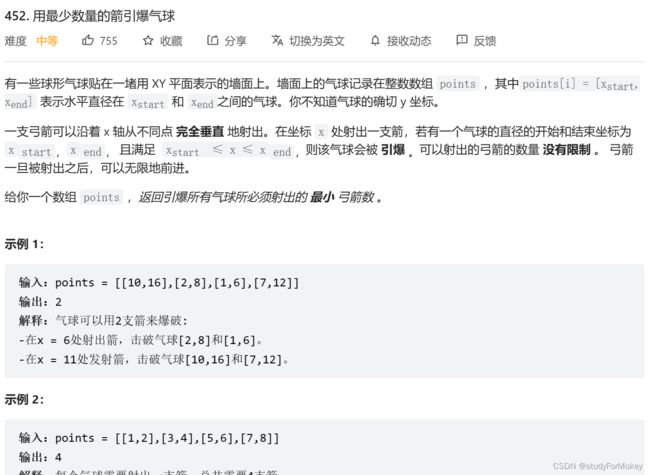
class Solution {
public int findMinArrowShots(int[][] points) {
int count = 1;
Arrays.sort(points,(a,b)->{
return Integer.compare(a[0]-b[0]);
});
for(int i=1;i<points.length;i++){
if(points[i][0]>points[i-1][1]){
count++;
}
else{
points[i][1] = Math.min(points[i][1],points[i-1][1]);
}
}
return count;
}
}
T435. 无重叠区间

思路分析:
排序(左边界从小到大),出现重叠就更新右边界
class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
int count=0;
Arrays.sort(intervals,(x,y)->{
return x[0]-y[0];
});
for(int i=1;i<intervals.length;i++){
if(intervals[i-1][1]>intervals[i][0]){
count++;
intervals[i][1] = Math.min(intervals[i-1][1],intervals[i][1]);
}
}
return count;
}
}
T763. 划分字母区间

class Solution {
public List<Integer> partitionLabels(String s) {
int[] sList = new int[26];
char[] ch = s.toCharArray();
List<Integer> res = new ArrayList<>();
for(int i = 0;i<ch.length;i++){
sList[ch[i]-'a'] = i;
}
int last = -1;
int maxIdx = 0;
for(int i = 0;i<ch.length;i++){
maxIdx = Math.max(maxIdx,sList[ch[i]-'a']);
if (i == maxIdx){
res.add(i-last);
last=i;
}
}
return res;
}
}
T56. 合并区间

class Solution {
public int[][] merge(int[][] intervals) {
Arrays.sort(intervals,(a,b)->Integer.compare(a[0],b[0]));
LinkedList<int[]> res = new LinkedList<>();
res.add(intervals[0]);
for(int i = 1;i<intervals.length;i++){
if(intervals[i][0]<=res.getLast()[1]){
int left = res.getLast()[0];
int right = Math.max(intervals[i][1],res.getLast()[1]);
res.removeLast();
res.add(new int[]{left,right});
}else{
res.add(intervals[i]);
}
}
return res.toArray(new int[res.size()][]);
}
}













