基于控制屏障函数的安全关键系统二次规划（适用于ACC）（Matlab代码实现）

     目录

1 概述

2 运行结果

3 参考文献

‍4 Matlab代码

1 概述

基于控制屏障函数的安全关键系统二次规划（适用于ACC）是一种用于自适应巡航控制（ACC）系统中的安全性优化方法。ACC是一种汽车自动驾驶技术，它通过感知前方车辆的距离和速度来调整车辆的速度，以维持与前车的安全距离。

控制屏障函数（Control Barrier Function，CBF）是一种数学工具，用于描述系统状态的约束和安全边界。在ACC系统中，CBF可以用来定义车辆的安全区域，即车辆与前车之间的安全距离范围。

基于CBF的二次规划方法可以通过最小化代价函数来优化ACC系统的性能和安全性。这个代价函数可以包括车辆速度、加速度、与前车的距离等参数，同时考虑到安全约束和性能要求。

通过解决二次规划问题，ACC系统可以在满足安全约束的前提下，实现车辆的自适应巡航控制。这种方法可以提供更高的安全性和可靠性，减少与前车的碰撞风险，并提高驾驶员的驾驶舒适度和体验。

需要注意的是，基于控制屏障函数的安全关键系统二次规划方法是一种技术，具体的实现和应用需要根据具体的ACC系统和实际需求进行定制和开发。同时，系统的安全性还需要考虑其他因素，如传感器精度、系统故障处理等，以确保ACC系统的可靠性和安全性。

2 运行结果

主函数部分代码：

clear all
clc
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%Objective: Adaptive Cruise Control (ACC) Simulation (A repeat of the result
%of the paper "Control Barrier Function Based Quadratic Programs for Safety
%Critical Systems (Page 3870)"
)%Author: Ming Li
%Date: March 2nd. 2022
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
global u_save
%% Initial Setup
%
 Note that [x(
1
) x(
2
) x(
3
)]==[v_f v_l D]%Initial distance between two vehicles is 150
%Intial velocity of the leading vehicle is 18;
%Intial velocity of the leading vehicle is 10;
Initial_position=[18 10 150];
t_span=[0:0.1:100];                                                        % Running time and interval
​
[Init_Par]=Initial_Parameter();
% [x] = ode4(@odefcn,t_span,Initial_position);
[x] = ode4(@odefcn,t_span,Initial_position);
% %% Ode45 plot
%
 figure(
1
)% plot(x.y(1,:),'b--','linewidth',2)
% hold on
% plot(x.y(2,:),'r--','linewidth',2)
% set(gca,'FontSize',23)
% set(gcf,'Position',[200,200,1000,800], 'color','w')
% xlabel('x1')
% ylabel('x2')
% legend('$v_{f}$','$v_{l}$','Interpreter','latex')
% grid on
​
%% Ode4 plot
figure(1)
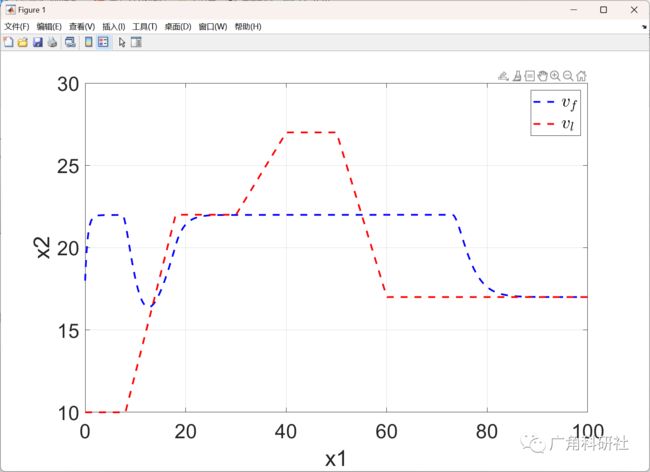
plot(t_span,x(:,1),'b--','linewidth',2)
hold on
plot(t_span,x(:,2),'r--','linewidth',2)
set(gca,'FontSize',23)
set(gcf,'Position',[200,200,1000,800], 'color','w')
xlabel('x1')
ylabel('x2')
legend('$v_{f}$','$v_{l}$','Interpreter','latex')
grid on
​
figure(2)
plot(x(:,3),'b--','linewidth',2)
set(gca,'FontSize',23)
set(gcf,'Position',[200,200,1000,800], 'color','w')
xlabel('x')
ylabel('D')
legend('$D$','Interpreter','latex')
grid on
​
%
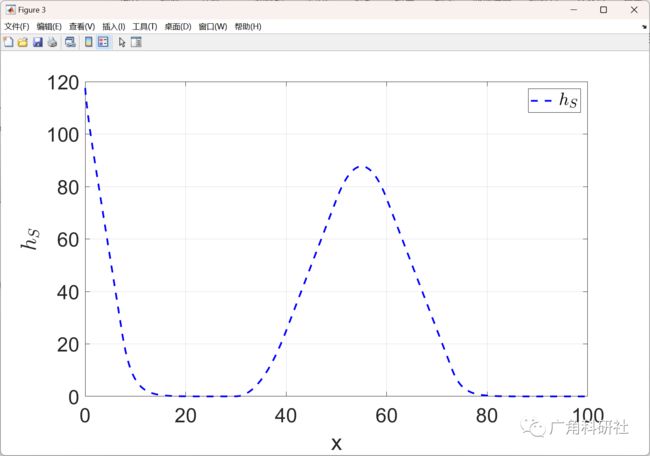
% Compute the CBFh_safe=x(:,3)-Init_Par.tau_d*x(:,1);
figure(3)
plot(t_span,h_safe,'b--','linewidth',2)
set(gca,'FontSize',23)
set(gcf,'Position',[200,200,1000,800], 'color','w')
xlabel('x')
ylabel('$h_{S}$','Interpreter','latex')
legend('$h_{S}$','Interpreter','latex')
grid on
​
%% Compute the control input
%
 d_x=diff(x(
:
,
1
));d_x=(x(2:end,1)-x(1:end-1,1))*10;
for i_u=1:size(x,1)-1
F_r(i_u)=Init_Par.f_0+Init_Par.f_1*x(1)+Init_Par.f_2*(x(1))^2;% Rolling resistance (force)
u_nodevi(i_u)=(d_x(i_u)*Init_Par.M+F_r(i_u));
u(i_u)=(d_x(i_u)*Init_Par.M+F_r(i_u))/Init_Par.M/Init_Par.a_g;
end
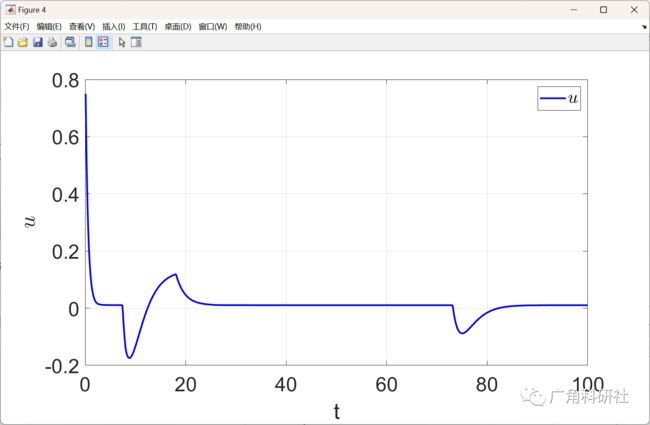
figure(4)
plot(t_span(2:end),u,'b-','linewidth',2)
set(gca,'FontSize',23)
set(gcf,'Position',[200,200,1000,800], 'color','w')
xlabel('t')
ylabel('$u$','Interpreter','latex')
legend('$u$','Interpreter','latex')
grid on
​
figure(5)
for i_u=1:size(x,1)-1
F_r(i_u)=Init_Par.f_0+Init_Par.f_1*x(1)+Init_Par.f_2*(x(1))^2;% Rolling resistance (force)
u_origin(i_u)=(u_save(1+(i_u-1)*4))/Init_Par.M/Init_Par.a_g;
end
plot(t_span(2:end),u_origin,'b-','linewidth',2)
set(gca,'FontSize',23)
set(gcf,'Position',[200,200,1000,800], 'color','w')
xlabel('t')
ylabel('$u$','Interpreter','latex')
legend('$u$','Interpreter','latex')
grid on
​
​
​
​

3 参考文献

​[1]赵向涛,阎妍,于双和等.基于屏障函数的船舶自适应控制[J].江苏大学学报(自然科学版),2021,42(06):715-720.

部分理论引用网络文献，若有侵权联系博主删除。