【数据挖掘·总复习】第八九章||K-means||K-中心点||密度聚类||知识点整理

step by step.

目录

1. K-means算法

（1） 聚集

（2） 距离

（3） K-means算法原理

        基本思想：

（4） K-means工作流程 

（5） 欧氏距离

 （6） 例题

（7） K-means算法特点

        a.优点

        b.缺点

2. K-中心点算法 

（2）K-中心点算法特点

        a. 优点

        b. 缺点 

3. 密度聚类算法

（1）DBSCAN算法

（2） 密度峰值算法

---

要看具体章节复习汇总请见

【scau数据挖掘·总复习】博客汇总||第一章~第九章+密度聚类_半段烟y9的博客-CSDN博客step by step.目录第二章第三章第四章第五章第六章第七章第八章、第九章、补充知识第二章【数据挖掘·总复习】第二章-数据预处理||详细整理||知识点+例题||考点有_半段烟y9的博客-CSDN博客详细复习资料https://blog.csdn.net/weixin_51159944/article/details/120444098第三章【数据挖掘·总复习】第三章-关联规则挖掘||Apriori||详细整理||知识点+例题||考点有_半段烟y9的博https://blog.csdn.net/weixin_51159944/article/details/122111501

自己辛苦总结的，点个赞鼓励一下啦~

---

1. K-means算法

（1） 聚集

将未知类别的样本分成若干簇。

（2） 距离

个体之间的距离。这里采用距离作为相似性度量。

（3） K-means算法原理

二者之间的距离比较小，那么它们之间的相似性就比较大。算法通常是由距离比较相近的对象组成簇，把得到紧凑而且独立的簇作为最终目标，因此将这类算法称为基于距离的聚类算法。

        基本思想：

首先指定需要划分的簇的个数k值;

然后随机地选择k个初始数据对象点作为初始的聚类中心;

第三，计算其余的各个数据对象与这k个初始聚类中心的相似性(这里采用距离作为相似性度量)，把数据对象划归到距离它最近的那个中心所处在的簇类中;

最后，调整新类并且重新计算出新类的中心。如果两次计算出来的聚类中心未曾发生任何的变化，那么就可以说明数据对象的调整己经结束。

（4） K-means工作流程 

对聚类中心采取的是迭代更新的方法，根据k个聚类中心，将周围的点划分成k个簇;在每一次的迭代中将重新计算的每个簇的质心，即簇中所有点的均值，作为下一次迭代的参照点。也就是说，每一次的迭代都会使选取的参照点越来越接近簇的几何中心也就是说簇心，所以目标函数如果越来越小，那么聚类的效果也会越来越好。 

（5） 欧氏距离

 （6） 例题

一维例题：

eg。

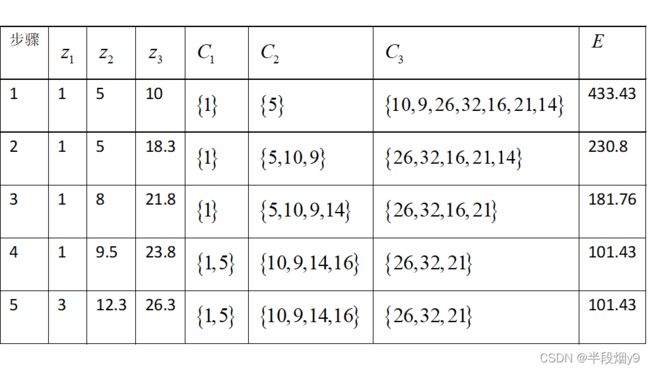
设有数据样本集合为X={1,5,10,9,26,32,16,21,14} ，将X 聚为3类，即k=3。随机选择前三个数值为初始的聚类中心，即 z1=1,z2=5,z3=10。（采用欧氏距离进行计算。）

解：

第一次迭代：按照三个聚类中心将样本集合分为三个{1},{5},{10,9,26,32,16,21,14} 。对于产生的簇分别计算平均值，得到平均值点填入第2步的 z1,z2,z3栏中。

第二次迭代：通过平均值调整对象所在的簇，重新聚类。即将所有点按距离平均值点1,5,18.3最近的原则重新分配，得到三个新的簇：{1},{5,10,9},{26,32,16,21,14} 。填入第2步的C1,C2,C3栏中。重新计算簇平均值点，得到新的平均值点为1,8,21.8。

以此类推，第五次迭代时，得到的三个簇与第四次迭代的结果相同，而且准则函数E收敛，迭代结束。结果如表所示。

 动手算就能懂的。

（7） K-means算法特点

        a.优点

  （1）K-means聚类算法是解决聚类问题的一种经典算法，算法简单、快速。

  （2）对处理大数据集，该算法是相对可伸缩的和高效率的，因为它的复杂度大约是O(nkt)，其中n是所有对象的数目，k是簇的数目，t是迭代的次数。通常地k<。这个算法经常以局部最优结束。

  （3）算法尝试找出使平方误差函数值最小的k个划分。当簇是密集的、球状或团状的，而簇与簇之间区别明显时，它的聚类效果较好。

        b.缺点

 （1）聚类个数k依赖于用户参数的指定；

 （2）基于距离的聚类算法只能发现球状簇，很难发现其他形状的簇。

 （3）初始中心随机选取，导致结果波动较大，稳定性较差。（因此有了K-中心点算法）

---

2. K-中心点算法 

K-中心点算法不采用簇中对象的均值作为参照点，而是在每个簇中选出一个实际的对象来代表该簇。

聚类结果的质量用代价函数来评估。

（1） 例题

eg。

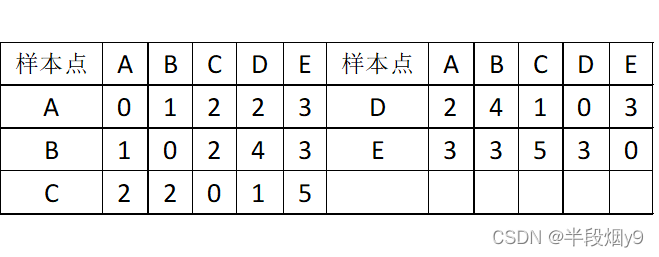
假如空间中的五个点A,B,C,D,E ，各点之间的距离关系如表9-1所示，根据所给的数据对其运行K-中心点算法实现聚类划分（设k=2）。

解：

（2）K-中心点算法特点

        a. 优点

对噪声点不敏感，具有较强的数据鲁棒性；

与数据输入顺序无关

        b. 缺点 

高耗时性；

通过迭代来寻求最佳的聚类中心点集时需要反复在非中心点对象与中心点对象之间进行最近邻搜索，从而产生大量非必需的重复计算。

---

3. 密度聚类算法

基于密度。 

（1）DBSCAN算法

核心点：圆心（内至少有m个点）

边界点：半径为r区域内（内点少于m）

噪音点：非上述点

 在半径为r的区域范围内所包含的样本点数量（包括自己），将任意2个距离小于r的核心点融合成一个聚类。

算法核心：寻找聚类并拓展类的过程。

（2） 密度峰值算法

过滤低密度区域的样本点，发现高密度区域的样本点。