双线性插值法
双线性插值法
- 前言
- 一、什么是插值?
- 2.常用的插值算法
- 3.最近邻法(Nearest Interpolation)
-
-
- 3.1总结
- 3.2双线性插值对应关系
- 4.单线性插值
- 5.双线性插值
-
前言
目标检测和语义分割的集大成者MaskRCNN提出了ROI Align,相比于Faster-RCNN中的ROIPooling,RA解决了区域不对称的问题,ROI Align引入了双线性插值的概念,同时它也是ROI Align的核心所在,在对于双线性插值进行讲解之前,我们先讨论常用的几种插值算法的概念。
一、什么是插值?
图片放大是图像处理中的一个特别基础的操作。在几乎每一个图片相关的项目中,从传统图像处理到深度学习,都有应用。生活里,和朋友通过微信传张图片,从图片发出,到朋友收到图片,查看图片,都会数次的的改变图像的尺寸,从而用到这个算法。但是大家只是在用这个算法,很少关注这个算法的实现细节:插值算法是如何工作的。
简单来说,插值指利用已知的点来“猜”未知的点,图像领域插值常用在修改图像尺寸的过程,由旧的图像矩阵中的点计算新图像矩阵中的点并插入,不同的计算过程就是不同的插值算法。
2.常用的插值算法
插值算法有很多种,这里列出关联比较密切的三种:
最近邻法(Nearest Interpolation):计算速度最快,但是效果最差。
双线性插值(Bilinear Interpolation):双线性插值是用原图像中4(22)个点计算新图像中1个点,效果略逊于双三次插值,速度比双三次插值快,属于一种平衡美,在很多框架中属于默认算法。
双三次插值(Bicubic interpolation):双三次插值是用原图像中16(44)个点计算新图像中1个点,效果比较好,但是计算代价过大。
3.最近邻法(Nearest Interpolation)
双线性插值法由原图中4个点计算新图中的1个点,在介绍计算过程前,需要先了解如何找到这4个点,双线性插值法找寻4个点的方式和最近邻法相似,这里顺带的了解下最近邻法的计算流程。
最近邻法实际上是不需要计算新图像矩阵中点的数值的,直接找到原图像中对应的点,将数值赋值给新图像矩阵中的点,根据对应关系找到原图像中的对应的坐标,这个坐标可能不是整数,这时候找最近的点进行插值。对应关系如下:

变量含义如下:

执行效果如图:

3.1总结
上图效果是最近邻法的计算过程示意图,由上图可见,最近邻法不需要计算只需要寻找原图中对应的点,所以最近邻法速度最快,但是会破坏原图像中像素的渐变关系,原图像中的像素点的值是渐变的,但是在新图像中局部破坏了这种渐变关系。
3.2双线性插值对应关系
双线性插值的对应公式和前面的最近邻法一样,不一样的是根据对应关系不再是找最近的1个点,而是找最近的4个点,如下图所示。

4.单线性插值
已知中P1点和P2点,坐标分别为(x1, y1)、(x2, y2),要计算 [x1, x2] 区间内某一位置 x 在直线上的y值

根据初中的知识,2点求一条直线公式(这是双线性插值所需要的唯一的基础公式)

经过简单整理成下面的格式:

首先看分子,分子可以看成x与x1和x2的距离作为权重,这也是很好理解的,P点与P1、P2点符合线性变化关系,所以P离P1近就更接近P1,反之则更接近P2。
现在再把公式中的分式看成一个整体,原式可以理解成y1与y2是加权系数,如何理解这个加权,要返回来思考一下,咱们先要明确一下根本的目的:咱们现在不是在求一个公式,而是在图像中根据2个点的像素值求未知点的像素值。这样一个公式是不满足咱们写代码的要求的。
现在根据实际的目的理解,就很好理解这个加权了,y1与y2分别代表原图像中的像素值,上面的公式可以写成如下形式:

5.双线性插值
已知Q11(x1,y1)、Q12(x1,y2)、Q21(x2,y1)、Q22(x2,y2),求其中点P(x,y)的值。

双线性插值是分别在两个方向计算了共3次单线性插值(x轴两次、y轴一次),如图所示,先在x方向求2次单线性插值,获得R1(x, y1)、R2(x, y2)两个临时点,再在y方向计算1次单线性插值得出P(x, y)(实际上调换2次轴的方向先y后x也是一样的结果)。
1.x方向单线性插值 直接带入前一步单线性插值最后的公式

2.y方向单线性插值
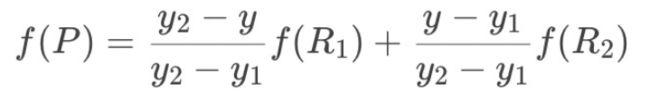
将第一步结果带入第二步。
回顾一下上面双线性插值对应关系的图,不难发现,在计算中有这样的关系:
![]()
在有些资料中,会写成权重的形式,上面的展开式是下面的权重表达式的正确求法
![]()
这种权重的表达式也不难理解,观察一下可以发现每个点的权重都和待求点和对角点的距离有关,比如f(Q11)的权重与f(Q22)的坐标有关、f(Q12)的权重与f(Q21)的坐标有关。