ros之旋转加平移公式
1.平移公式
用到的公式:
平移公式:
dstX 1 0 i x
dstY = 0 1 j * y
1 0 0 1 1
构建变换矩阵
matrix = np.array([
[1, 0, b[0]],
[0, 1, b[1]],
[0, 0, 1],
])
"""
在B坐标系中,有点P,对于B坐标系而言,P点的坐标为(3,4).
有A坐标系,B坐标系的原点在A坐标系中的位置为(3,2),且B坐标系的X,Y轴分别和A坐标系的两两平行。
求解: P点在A坐标系中的位置。
平移公式:
dstX 1 0 i x
dstY = 0 1 j * y
1 0 0 1 1
"""
import numpy as np
# 已知的值
# p点在b坐标系中的位置
pb = (3, 4)
# b坐标系的原点在a坐标系中的位置
b = (3, 2)
# 求救 p 在a坐标系中的位置
matrix = np.array([
[1, 0, b[0]],
[0, 1, b[1]],
[0, 0, 1],
])
point = np.array([
[pb[0]],
[pb[1]],
[1]
])
pa = matrix.dot(point)
print(pa)
result = (pa[0, 0], pa[1, 0])
print(result)2.旋转公式
用到的公式:
dstX = cos(theta) -sin(theta) * x
dstY sin(theta) cos(theta) * y
构建变换矩阵
matrix = np.array([
[cos(theta), -sin(theta)],
[sin(theta), cos(theta)]
])
"""
在B坐标系中,有点P,对于B坐标系而言,P点的坐标为(sqrt(12), 2).
有A坐标系,A坐标系和B坐标系原点重合,B坐标系相对于A坐标系旋转了30度.
求解: P点在A坐标系中的位置
变换公式:
dstX = cos(theta) -sin(theta) * x
dstY sin(theta) cos(theta) y
"""
import numpy as np
from math import sqrt, sin, cos, radians
# p在b坐标系中的位置
pb = (sqrt(12), 2)
# b坐标系相对于a坐标系旋转的角度
theta = radians(30)
# 构建变换矩阵
matrix = np.array([
[cos(theta), -sin(theta)],
[sin(theta), cos(theta)]
])
point = np.array([
[pb[0]],
[pb[1]]
])
# 求解
pa = matrix.dot(point)
print(pa)
3.旋转加平移公式
注意: 如需要推导交换矩阵公式的时候先推导旋转后推导平移
用到的公式:
dstX cos(theta) -sin(theta) deltaX x
dstY = sin(theta) cos(theta) deltaY * y
1 0 0 1 1
构建变换矩阵
matrix = np.array([
[cos(theta), -sin(theta), delta[0]],
[sin(theta), cos(theta), delta[1]],
[0, 0, 1],
])
"""
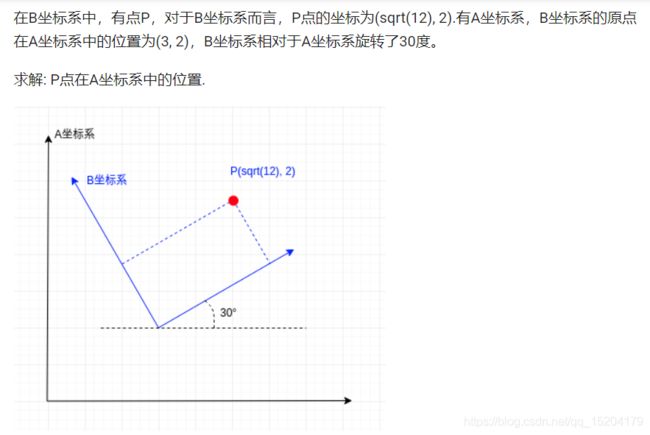
在B坐标系中,有点P,对于B坐标系而言,P点的坐标为(sqrt(12), 2).
有A坐标系,B坐标系的原点在A坐标系中的位置为(3, 2),
B坐标系相对于A坐标系旋转了30度。
求解: P点在A坐标系中的位置.
变换矩阵
dstX cos(theta) -sin(theta) deltaX x
dstY = sin(theta) cos(theta) deltaY * y
1 0 0 1 1
"""
import numpy as np
from math import sqrt, sin, cos, radians
# p点在b坐标系中的位置
pb = (sqrt(12), 2)
# b坐标系相对于a坐标系的移动
delta = (3, 2)
# b坐标系相对于a坐标系的旋转
theta = radians(30)
# 变换矩阵
matrix = np.array([
[cos(theta), -sin(theta), delta[0]],
[sin(theta), cos(theta), delta[1]],
[0, 0, 1],
])
point = np.array([
[pb[0]],
[pb[1]],
[1]
])
# p在a中的表达
pa = matrix.dot(point)
print(pa)
4.双连杆
# 变换矩阵
Tba = np.array([
[cos(theta), -sin(theta), delta[0]],
[sin(theta), cos(theta), delta[1]],
[0, 0, 1],
])
4.1 做法1
"""
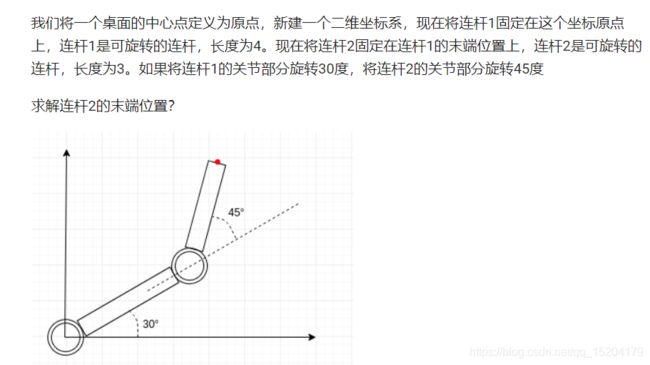
我们将一个桌面的中心点定义为原点,新建一个二维坐标系,现在将连杆1固定在这个坐标原点上,
连杆1是可旋转的连杆,长度为4。
现在将连杆2固定在连杆1的末端位置上,
连杆2是可旋转的连杆,长度为3。
如果将连杆1的关节部分旋转30度,
将连杆2的关节部分旋转45度
求解连杆2的末端位置?
变换矩阵
dstX cos(theta) -sin(theta) deltaX x
dstY = sin(theta) cos(theta) deltaY * y
1 0 0 1 1
"""
import numpy as np
from math import sqrt, sin, cos, radians
len1 = 4
len2 = 3
# p点在连杆2坐标系中的位置
pb = (len2, 0)
# 连杆2坐标系相对于连杆1坐标系的移动
delta = (len1, 0)
# 连杆2坐标系相对于连杆1坐标系的旋转
theta = radians(45)
# 变换矩阵
Tba = np.array([
[cos(theta), -sin(theta), delta[0]],
[sin(theta), cos(theta), delta[1]],
[0, 0, 1],
])
point = np.array([
[pb[0]],
[pb[1]],
[1]
])
# pb转pa
pa = Tba.dot(point)
print(pa)
# A坐标系转换为桌面坐标系
# 变换矩阵
theta = radians(30)
Taw = np.array([
[cos(theta), -sin(theta), 0],
[sin(theta), cos(theta), 0],
[0, 0, 1],
])
pw = Taw.dot(pa)
print(pw)
4.2 做法2
"""
我们将一个桌面的中心点定义为原点,新建一个二维坐标系,现在将连杆1固定在这个坐标原点上,
连杆1是可旋转的连杆,长度为4。
现在将连杆2固定在连杆1的末端位置上,
连杆2是可旋转的连杆,长度为3。
如果将连杆1的关节部分旋转30度,
将连杆2的关节部分旋转45度
求解连杆2的末端位置?
变换矩阵
dstX cos(theta) -sin(theta) deltaX x
dstY = sin(theta) cos(theta) deltaY * y
1 0 0 1 1
"""
import numpy as np
from math import sqrt, sin, cos, radians
len1 = 4
len2 = 3
theta1 = radians(30)
theta2 = radians(45)
# 获取B坐标系转A坐标系的变换矩阵
Tba = np.array([
[cos(theta2), -sin(theta2), len1],
[sin(theta2), cos(theta2), 0],
[0, 0, 1],
])
# 获取A坐标系转W坐标系的变换矩阵
Taw = np.array([
[cos(theta1), -sin(theta1), 0],
[sin(theta1), cos(theta1), 0],
[0, 0, 1],
])
# B坐标系转转W坐标系的变换矩阵
Tbw = Taw.dot(Tba)
# p点在B坐标系中的位置
point = np.array([
[len2],
[0],
[1]
])
# 求解p点在W坐标系中的位置
pw = Tbw.dot(point)
print(pw)
5.三连杆
from math import radians,cos,sin
import numpy as np
# p点在c坐标系中的位置
l3=(2,0)
# 连杆3的关节部分旋转-90度
t3=radians(-90)
# c坐标在b坐标移动的位置
l2=(3,0)
#连杆2的关节部分旋转45度
t2=radians(45)
# b坐标在a坐标移动的位置
l1=(4,0)
#连杆1的关节部分旋转30度
t1=radians(30)
#c坐标转换b坐标
bct=np.array([
[cos(t3),-sin(t3),l2[0]],
[sin(t3),cos(t3),l2[1]],
[0,0,1]
])
#b坐标转换a坐标
bat=np.array([
[cos(t2),-sin(t2),l1[0]],
[sin(t2),cos(t2),l1[1]],
[0,0,1]
])
#a坐标转换w坐标
awt=np.array([
[cos(t1),-sin(t1),0],
[sin(t1),cos(t1),0],
[0,0,1]
])
pc=np.array([
[l3[0]],
[l3[1]],
[1]
])
awt.dot(bat).dot(bct).dot(pc)