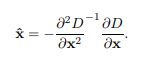论文笔记：SIFT（Scale-invariant feature transform 尺度不变特征变换）

1.SIFT介绍

1.1.介绍

SIFT（Scale-invariant feature transform 尺度不变特征变换）图像特征匹配，即使图像有旋转、模糊、尺度、亮度的变化，即使使用不同的相机，即使图像拍摄的角度不同，SIFT总能检测到稳定的特征点。SIFT是人工设计特征的一个巅峰。

SIFT算法由加拿大英属哥伦比亚大学教授David Lowe 于 1999 年发表于会议ICCV ，原论文Object recognition from local scale-invariant features ，David Lowe 是唯一作者。

广为人知的被引用更多的是2004年发表于期刊IJCV的完善版 Distinctive image features from scale-invariant keypoints。 本文就是基于此论文翻译总结的。

2020年3月6日专利到期，可以免费试用。OpenCV里有。

2.算法简介

包括下面四部分：
1.尺度空间极值检测-关键点检测：使用 高斯差分difference-of-Gaussian 方法识别潜在的关键点（特征点），其中这些特征点对尺度、方向是不变的。
2.关键点确定：对每个候选的关键点，最终确定其是否合适及位置和尺度。
3.关键点方向指定：一个或者多个方向基于图片的梯度方向指定到每个关键点（keypoint location）。
4.关键点描述符：梯度、尺度、位置都确定了。然后转换成一种表达，它能有效应对图片扭曲、光照等情况。
5.最终检测时，会有一个数据库，里面存了大量训练的图片特征数据，然后用检测的图片和数据库中特征比较，发现足够匹配的特征就可以识别出来，至少有3个特征匹配吧。
下面章节会就此四部分分别介绍下。

3.尺度空间极值检测-关键点检测

本节的主要目的是完成下图的b图，找到一堆关键点（keypoint），如下图黄色箭头所示，包含尺度大小、方向、位置。主要是通过difference-of-Gaussian 方法。

3.1.高斯差分difference-of-Gaussian

输入图片I（x,y）。高斯函数G（x,y,ó）。
图片的尺度空间函数L（x,y,ó）等输入图片I（x,y）与高斯函数G（x,y,ó）的卷积。如下所示：

高斯差分D（x,y,ó）:由两个邻近的尺度差分计算所得。两个邻近的尺度由一个常数相乘因子k分割。公式如下：

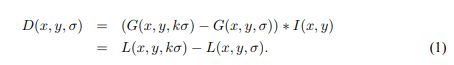
参考热传导方程，得到

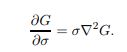
＠G/＠ó可以近似等于相邻尺度kó与ó的差分，故有下式:

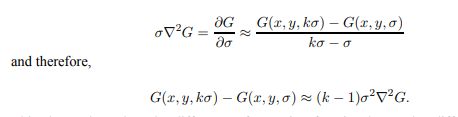
Mikolajczyk (2002) 发现的极大极小值，相比于梯度方法、Hessian、Harris corner等方法，可以产生非常稳定的图片特征。上式刚好使高斯差分D（x,y,ó）函数满足。其中k-1可以看做一个常数，比如取。

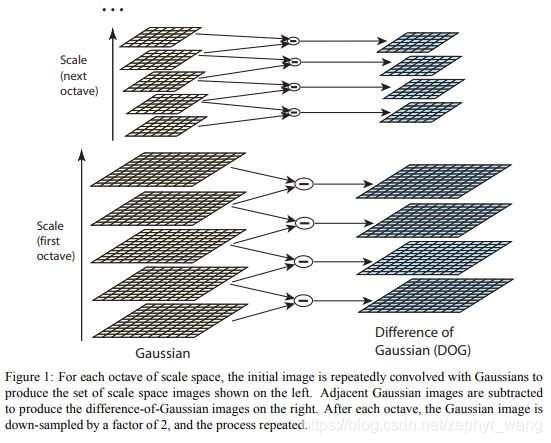
下图是高斯差分D（x,y,ó）示意图，左边是一堆间隔的尺度空间图片，相邻的两个相减产生高斯差分图像（右侧的）。比如下图是两个scale（s=2）,,对于每个octave产生5（s+3）张图片（左侧的），相邻的相减产生右侧的高斯差分图。不断的用两倍的ó来产生scale。下面章节会说到，产生3个scale就可以了。

3.2.本地极值检测

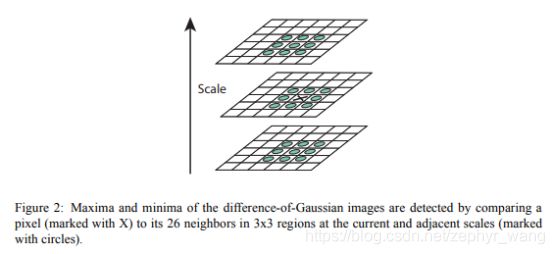
如下图所示，每个高斯差分和本层附件的8个点以及上下相邻尺度的各9个点，总共26（2*9+8）个点比较，选出最大值或最小值。

3.3.在尺度上的采用频率

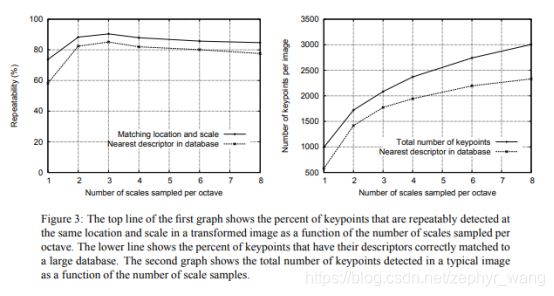
即分析几个scale就可以了，从下图（左图）看到，3个scale就效果很好了。横轴是scale的数量，纵轴代表在图片的相同位置和尺寸下重复检测到的特征点比例。

3.4.在空间域的采用频率

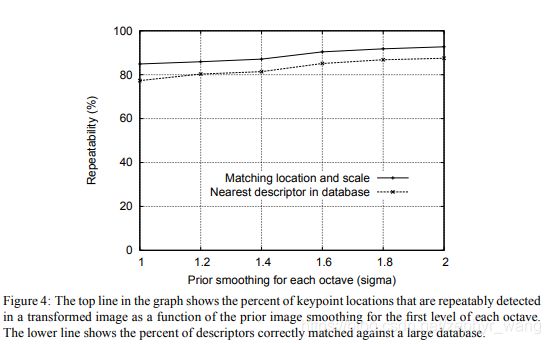
主要是分析ó的值，如下图，可以看到取ó=1.6就可以了。横轴是ó的大小，纵轴是特征位置（keypoint location）被重复检测到的比例。

4.关键点确定

如前所述，本节主要是针对上一步产生的候选关键点进行筛选。
对D（x,y,ó）用了泰勒展开式。其中D及其衍生是基于采样点评估的，是基于采样点的偏移量。

上式求导算极值，得到。

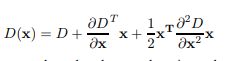
进而得到：

在第3章节的图c就是去除了小于0.03后得到的。

4.1.去除边缘的响应

高斯差分会产生强烈的边缘响应，所以需要去除。高斯差分中一个不明显的波峰在其沿着边缘会产生大的主曲率，却有小的正交方向。主曲率可以从一个2*2的Hessian 矩阵 H计算得到，H公式如下：

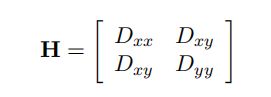
可以不用直接计算H，而是计算比率r，比率容易计算。


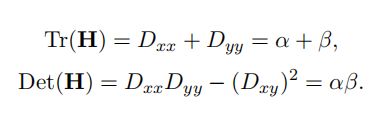
从而，

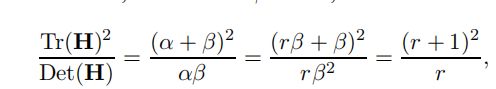
最终有下式,只要满足下式的关键点就不去除，实验发现取r=10.

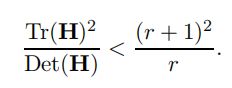
在第3章节的图d就是去除了主曲率不符合条件后得到的。

5.关键点方向指定

对于图片L（x,y）,梯度大小定义为m（x,y），方向定义为θ（x，y），它们可以由像素的差分计算所得，公式如下：

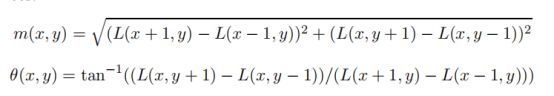
6.关键点描述符（keypoint descriptor）

6.1.描述符的形式

就是著名的下图了，左图是每个采样点的梯度大小和方向，圆圈是高斯圈。每个采样依据梯度大小、高斯圈形成方向直方图，然后加总形成右图，其中右图每个箭头的长度代表该区域某方向上梯度大小的和。

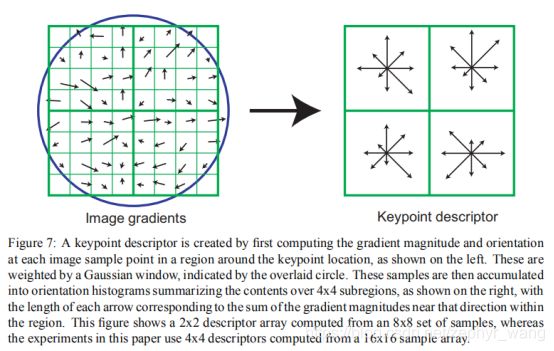
6.2.描述符的测试

从下图看到采用4*4descriptor、8 orientation可以产生良好的效果，本论文采用的此方式，会产生一个带有128维的特征向量。

7.物体检测案例

如下图，及时物体被挡在一部分，也是可以检测到的。