机器学习实战13-超导体材料的临界温度预测与分析(决策树回归,梯度提升回归,随机森林回归和Bagging回归)
大家好,我是微学AI,今天给大家介绍一下机器学习实战13-超导体材料的临界温度预测与分析(决策树回归,梯度提升回归,随机森林回归和Bagging回归),这几天引爆网络的科技大新闻就是韩国科研团队宣称发现了室温超导材料-LK-99,这种材料在常压情况下,127摄氏度就可以达到超导临界点,他们还在推特上建立的账号,发布了相关视频。
上个世纪到现在科学家都在实验寻找超导材料,如果实现室温超导,那将是科学家们梦寐以求的追求,可以毫不夸张的说是“第四次工业革命”,人类的整个工业体系将被重塑。
目录
室温超导介绍
超导体材料的临界温度
超导体的临界温度的预测
超导体实验数据
超导体数据分析
临界温度预测与代码
总结

室温超导介绍
室温超导是指在常规的环境条件下,材料能够表现出超导电性,材料的电阻为0。在传统超导材料中,需要将材料冷却到极低的温度(通常接近绝对零度)才能实现超导。但室温超导的概念是指找到一种材料或结构,使之在室温下仍然能够以零电阻的方式传导电流。
要实现室温超导,研究人员面临着许多挑战。首先,他们需要寻找具有适当电子结构和相互作用的材料,以便在室温下形成库珀电子对。其次,他们需要克服材料在常温下的热震荡和散射问题,以确保电子对能够在材料中长距离传输而不被干扰或损失。
本次韩国论文表明,韩国科学家发现的“改性铅磷灰石晶体结构”,成分为 P b ( 10 − x ) C u x ( P O 4 ) 6 O Pb(10-x)Cux(PO_4)_{6}O Pb(10−x)Cux(PO4)6O合成超导材料,一共分为三步:
第一步,按照配比合成黄铅矿 P b ( S O 4 ) O Pb(SO_{4})O Pb(SO4)O;
第二步,合成磷化亚铜晶体 C u 3 P Cu_{3}P Cu3P;
第三步,生成常温常压超导体 P b ( 10 − x ) C u x ( P O 4 ) 6 O Pb(10-x)Cux(PO_4)_{6}O Pb(10−x)Cux(PO4)6O;
现在多个国家与实验室正在复现这个成果,不过这种材料是否具有超导性还有待观察,只能说这是一次在寻找超导材料的历程中更迈进了一步,科研之路还是很漫长的,大家还是抱着理性的心态看待这件事。
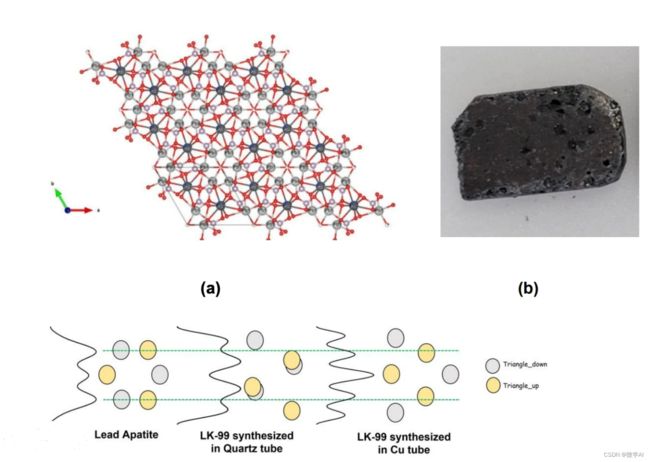
下面针对超导的临界温度进行预测分析,让大家更加熟悉超导材料为什么寻找如此困难。
超导体材料的临界温度
超导体的临界温度(Critical Temperature,Tc)是指材料在该温度以下开始表现出超导性质。超导体在低温下具有特殊的电子行为,包括零电阻和磁场排斥效应(Meissner 效应)。临界温度是判断一个材料是否能够实现超导的重要参数。
传统的超导体通常具有较低的临界温度,需要将其冷却至接近绝对零度(-273.15摄氏度或0开尔文)才能实现超导。例如,铅的临界温度约为7.2开尔文(-265.95摄氏度),铜氧化物高温超导体的临界温度可达到几十开尔文。
高温超导体是指临界温度较传统超导体更高的材料。1986年,发现了第一种具有相对较高临界温度(超过液氮沸点77开尔文)的铜氧化物超导体,这一发现引起了科学界的轰动。随后,研究人员发现了许多其他高温超导体,且临界温度进一步提高。目前,已经发现的最高临界温度约为138开尔文(-135摄氏度)。
提高超导体的临界温度是超导研究的一个重要目标。因为高温超导体相对于传统超导体,它们不需要极端低温条件就能够实现超导。这意味着更容易实现制冷和工程应用,使得超导技术更具实用性。
超导体的临界温度的预测
超导体的临界温度的预测与分析是超导研究领域的重要课题之一,其具有重要的理论和实际意义。关于超导体的研究历程:
1.简介和历史:超导现象最早在1911年被荷兰物理学家海克·卡末林·奥尼斯发现,他观察到汞在低温下电阻突然消失。经过多年的研究,科学家们发现了多种超导体,包括低温超导体和高温超导体。
2.BCS理论:低温超导体的超导机制可由BCS理论解释,该理论由约翰·巴丁, 勒尔莫·库珀和罗伯特·肖利提出。BCS理论认为,超导性是由电子-声子相互作用引起的。该理论成功预测了多种低温超导体的临界温度。
3.高温超导体:1986年,瑞士IBM实验室的J.G. Bednorz和K.A. Müller发现了第一个高温超导体(铜氧化物)。高温超导体的临界温度较低温超导体更高,但其超导机制至今仍不完全清楚。
4.材料设计:预测和提高超导体的临界温度是超导研究的重要目标之一。科学家们通过理论计算、实验和模拟等方法,探索不同材料的超导性能。其中一种方法是通过调整晶格结构、化学成分以及引入掺杂物,来寻找具有更高临界温度的超导体。
5.硬件应用:超导体的临界温度直接关系到其在实际应用中的可行性。高临界温度超导体能在较高温度下实现超导,降低制冷成本,因此被广泛应用于磁共振成像(MRI)、磁悬浮列车、电力输电和电能储存等领域。
超导体实验数据
这里整理了关于超导体实验数据,数据下载地址:
链接:https://pan.baidu.com/s/1vhu3rZ1ruBOWddfiOFV6XQ?pwd=yl26
提取码:yl26
该数据的字段比较多,我详细介绍一下每个字段的含义:
number_of_elements: 包含的元素数量
mean_atomic_mass: 平均原子质量
wtd_mean_atomic_mass: 权重平均原子质量
gmean_atomic_mass: 几何平均原子质量
wtd_gmean_atomic_mass: 权重几何平均原子质量
entropy_atomic_mass: 原子质量的熵
wtd_entropy_atomic_mass: 权重的原子质量熵
range_atomic_mass: 原子质量的范围
wtd_range_atomic_mass: 权重的原子质量范围
std_atomic_mass: 原子质量的标准差
wtd_std_atomic_mass: 权重的原子质量标准差
mean_fie: 平均电离能
wtd_mean_fie: 权重平均电离能
gmean_fie: 几何平均电离能
wtd_gmean_fie: 权重几何平均电离能
entropy_fie: 电离能的熵
wtd_entropy_fie: 权重的电离能熵
range_fie: 电离能的范围
wtd_range_fie: 权重的电离能范围
std_fie: 电离能的标准差
wtd_std_fie: 权重的电离能标准差
mean_atomic_radius: 平均原子半径
wtd_mean_atomic_radius: 权重平均原子半径
gmean_atomic_radius: 几何平均原子半径
wtd_gmean_atomic_radius: 权重几何平均原子半径
entropy_atomic_radius: 原子半径的熵
wtd_entropy_atomic_radius: 权重的原子半径熵
range_atomic_radius: 原子半径的范围
wtd_range_atomic_radius: 权重的原子半径范围
std_atomic_radius: 原子半径的标准差
wtd_std_atomic_radius: 权重的原子半径标准差
mean_Density: 平均密度
wtd_mean_Density: 权重平均密度
gmean_Density: 几何平均密度
wtd_gmean_Density: 权重几何平均密度
entropy_Density: 密度的熵
wtd_entropy_Density: 权重的密度熵
range_Density: 密度的范围
wtd_range_Density: 权重的密度范围
std_Density: 密度的标准差
wtd_std_Density: 权重的密度标准差
mean_ElectronAffinity: 平均电子亲和能
wtd_mean_ElectronAffinity: 权重平均电子亲和能
gmean_ElectronAffinity: 几何平均电子亲和能
wtd_gmean_ElectronAffinity: 权重几何平均电子亲和能
entropy_ElectronAffinity: 电子亲和能的熵
wtd_entropy_ElectronAffinity: 权重的电子亲和能熵
range_ElectronAffinity: 电子亲和能的范围
wtd_range_ElectronAffinity: 权重的电子亲和能范围
std_ElectronAffinity: 电子亲和能的标准差
wtd_std_ElectronAffinity: 权重的电子亲和能标准差
mean_FusionHeat: 平均熔化热
wtd_mean_FusionHeat: 权重平均熔化热
gmean_FusionHeat: 几何平均熔化热
wtd_gmean_FusionHeat: 权重几何平均熔化热
entropy_FusionHeat: 熔化热的熵
wtd_entropy_FusionHeat: 权重的熔化热熵
range_FusionHeat: 熔化热的范围
wtd_range_FusionHeat: 权重的熔化热范围
std_FusionHeat: 熔化热的标准差
wtd_std_FusionHeat: 权重的熔化热标准差
mean_ThermalConductivity: 平均热导率
wtd_mean_ThermalConductivity: 权重平均热导率
gmean_ThermalConductivity: 几何平均热导率
wtd_gmean_ThermalConductivity: 权重几何平均热导率
entropy_ThermalConductivity: 热导率的熵
wtd_entropy_ThermalConductivity: 权重的热导率熵
range_ThermalConductivity: 热导率的范围
wtd_range_ThermalConductivity: 权重的热导率范围
std_ThermalConductivity: 热导率的标准差
wtd_std_ThermalConductivity: 权重的热导率标准差
mean_Valence: 平均价电子数
wtd_mean_Valence: 权重平均价电子数
gmean_Valence: 几何平均价电子数
wtd_gmean_Valence: 权重几何平均价电子数
entropy_Valence: 价电子数的熵
wtd_entropy_Valence: 权重的价电子数熵
range_Valence: 价电子数的范围
wtd_range_Valence: 权重的价电子数范围
std_Valence: 价电子数的标准差
wtd_std_Valence: 权重的价电子数标准差
critical_temp: 临界温度
超导体数据分析
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sb
import tensorflow as tf
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error as mse
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import GradientBoostingRegressor, RandomForestRegressor, BaggingRegressor
# 加载数据
dataFrame = pd.read_csv('train.csv')
featuresNeeded = dataFrame.columns[:-1]
features = np.array(dataFrame[featuresNeeded])
targets = np.array(dataFrame['critical_temp'])
# 对特征向量进行标准化,以便进行PCA和进一步处理
stdc = StandardScaler()
features = stdc.fit_transform(features)
pca = PCA(n_components=2)
pca.fit(features)
dimReducedFrame = pca.transform(features)
# 转换为DataFrame并绘图
dimReducedFrame = pd.DataFrame(dimReducedFrame)
dimReducedFrame = dimReducedFrame.rename(columns={0: 'V1', 1: 'V2'})
dimReducedFrame['critical_temp'] = targets
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
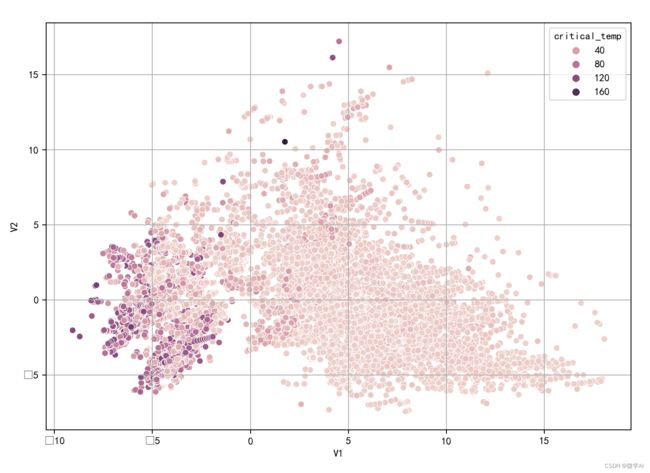
# 绘制散点图
plt.figure(figsize=(10, 7))
sb.scatterplot(data=dimReducedFrame, x='V1', y='V2', hue='critical_temp')
plt.grid(True)
plt.show()
# 绘制第一主成分与Tc之间的关系图
plt.figure(figsize=(15, 5))
plt.subplot(1, 2, 1)
sb.regplot(data=dimReducedFrame, x='V1', y='critical_temp', color='blue')
plt.title('Tc与第一主成分的关系')
# 绘制第二主成分与Tc之间的关系图
plt.subplot(1, 2, 2)
sb.regplot(data=dimReducedFrame, x='V2', y='critical_temp', color='blue')
plt.title('Tc与第二主成分的关系')
plt.show()
临界温度预测与代码
下面我将对给定数据集中的温度数据进行探索和分析,并使用线性回归、决策树回归、梯度提升回归、随机森林回归和Bagging回归等模型进行预测和性能评估。
# 对目标值进行归一化
maxTc = max(targets)
targets = targets / 1
# 将数据拆分为训练集和测试集
xTrain, xTest, yTrain, yTest = train_test_split(features, targets, test_size=0.2, random_state=42)
# 定义用于评估模型性能的函数
def PerformanceCalculator(trueVals, predVals, name):
plt.plot([0, 0.001, 0.01, 1], [0, 0.001, 0.01, 1], color='blue')
plt.scatter(trueVals, predVals, color='red')
er = mse(trueVals, predVals)
er = pow(er, 0.5)
er = int(er * 10000) / 10000
plt.title('RMSE: ' + str(er) + ' for ' + name)
plt.show()
# 使用线性回归进行分析
lr = LinearRegression()
lr.fit(xTrain, yTrain)
predictions = lr.predict(xTest)
PerformanceCalculator(yTest, predictions, '线性回归')
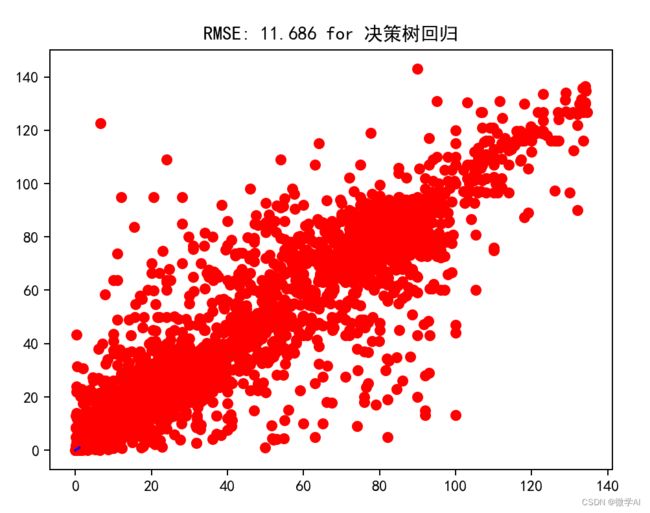
# 使用决策树进行分析
lr = DecisionTreeRegressor()
lr.fit(xTrain, yTrain)
predictions = lr.predict(xTest)
PerformanceCalculator(yTest, predictions, '决策树回归')
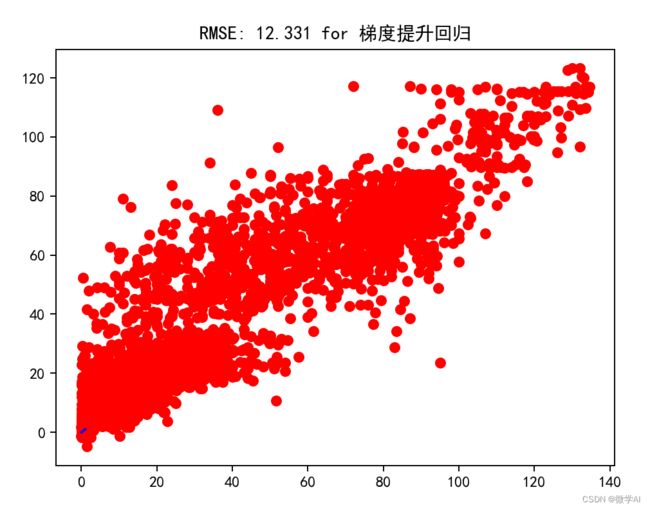
# 使用梯度提升回归进行分析
lr = GradientBoostingRegressor()
lr.fit(xTrain, yTrain)
predictions = lr.predict(xTest)
PerformanceCalculator(yTest, predictions, '梯度提升回归')
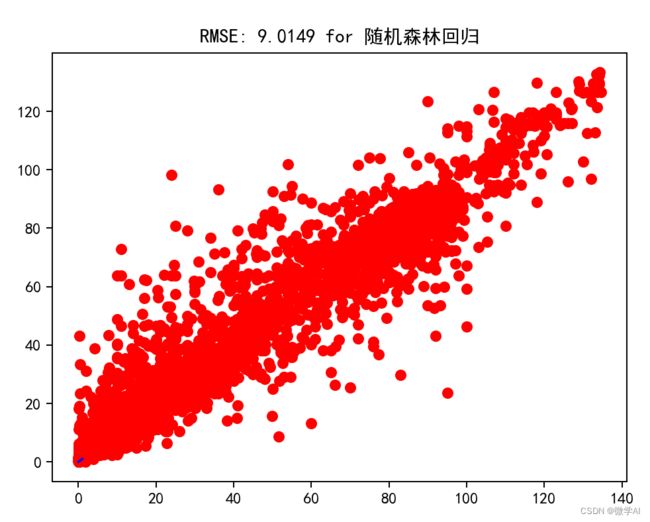
# 使用随机森林进行分析
lr1 = RandomForestRegressor()
lr1.fit(xTrain, yTrain)
predictions = lr1.predict(xTest)
PerformanceCalculator(yTest, predictions, '随机森林回归')
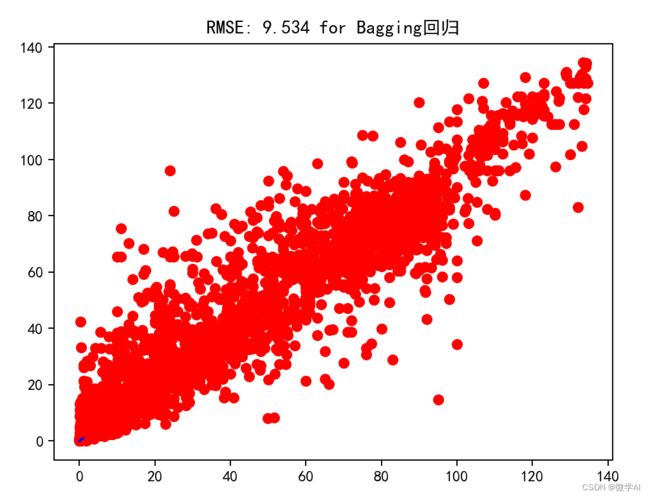
# 使用Bagging回归进行分析
lr = BaggingRegressor()
lr.fit(xTrain, yTrain)
predictions = lr.predict(xTest)
PerformanceCalculator(yTest, predictions, 'Bagging回归')
#
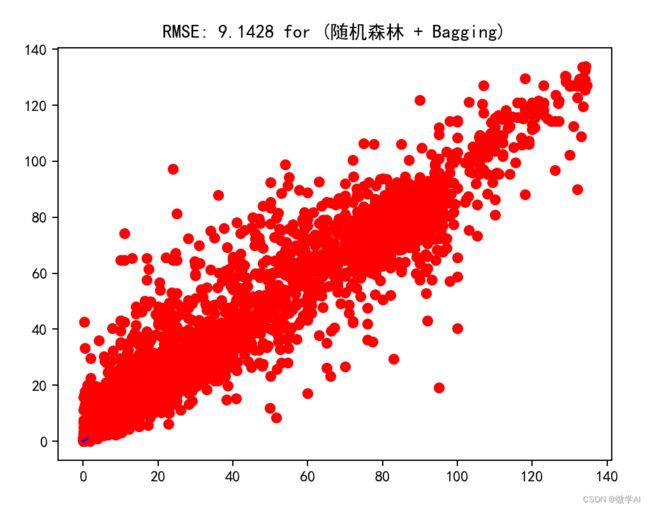
# 使用集成方法进行预测
pred1 = lr1.predict(xTest)
pred2 = lr.predict(xTest)
predictions = (pred1 + pred2)/ 2
# 评估集成模型性能
PerformanceCalculator(yTest, predictions, '(随机森林 + Bagging)')
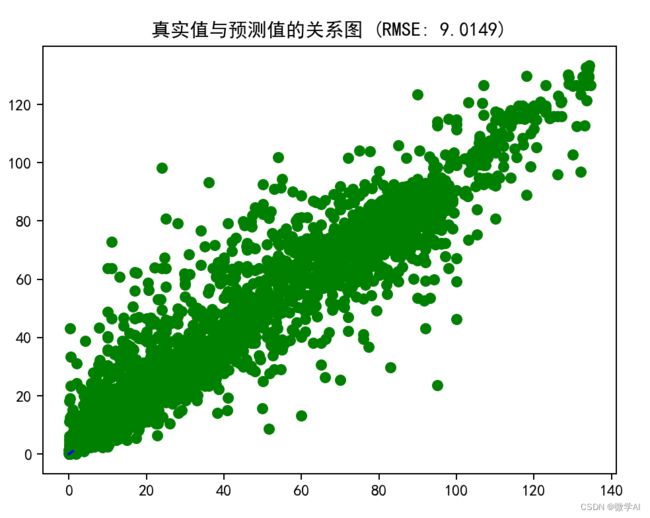
# 绘制真实值与预测值的关系图
ylab = yTest
predVals = lr1.predict(xTest)
plt.plot([0, 0.001, 0.01, 1], [0, 0.001, 0.01, 1], color='blue')
plt.scatter(ylab, predVals, color='green')
er = mse(ylab, predVals)
er = pow(er, 0.5)
er = int(er * 10000) / 10000
plt.title('真实值与预测值的关系图 (RMSE: ' + str(er) + ')')
plt.show()
总结
超导体临界温度的预测与分析是超导研究的重要方向。通过理论、实验和模拟等手段,科学家们致力于寻找新的超导材料和优化现有材料,以提高超导体的临界温度,推动超导技术在各个领域的应用。
如果未来室温超导体能够发现与应用,那在多个领域都能起到翻天覆地的变化。未来超导体的应用:
磁共振成像(MRI):超导磁体在MRI设备中作为强大的磁场源,用于获取人体内部的高清影像,用于医学诊断。
加速器和粒子物理实验:超导磁体广泛应用于加速器、环形对撞机等粒子物理实验中,用于产生强大的磁场以加速和操控高能粒子束。
磁悬浮列车:超导磁体可以产生强大的磁力,用于磁悬浮列车的悬浮和推进,使列车无接触地高速运行,具有较低的摩擦和能耗。
能源传输和储存:超导体可用于电力输电线路,通过降低电阻减少能量损失;同时,超导体还可以应用于超导蓄能器等能量存储装置,用于平衡电网能量波动。
可控核聚变:可控核聚变是一种将轻元素核融合并释放出巨大能量的过程,被视为清洁、可持续的能源解决方案之一。