动态规划之树形DP

树形DP

何为树形DP

树形DP是指在“树”这种数据结构上进行的动态规划：给出一颗树，要求以最少的代价（或取得最大收益）完成给定的操作。通常这类问题规模比较大，枚举算法效率低，无法胜任，贪心算法不能求得最优解，因此需要用动态规划进行求解。

在树上做动态规划显得非常合适，因为树本身有“子结构”性质（树和子树），具有递归性，符合DP性质。相比线性DP，树形DP的状态转移方程更加直观。

树形动态规划（Tree DP）是一种动态规划算法，在处理树状结构（例如树、森林、有向无环图等）上的问题时非常常见和有效。树形动态规划通过将问题拆解为子问题，并利用子问题的解来求解更大规模的问题。

在树形动态规划中，我们需要定义一个适合的状态和状态转移方程。一般来说，状态可以定义为以当前节点为根的子树的某种性质，例如最大路径和、最长路径长度、最大权值和等等。而状态转移方程则描述了如何由子节点的状态计算当前节点的状态。

树形动态规划的典型做法是使用深度优先搜索（DFS）遍历整个树，在遍历过程中进行状态的计算和更新。通过递归地计算子节点的状态，并将其传递给父节点，可以得到整个树的最终状态。

在实现树形动态规划时，需要注意避免重复计算，可以使用记忆化搜索或者自底向上的方式进行计算。此外，还要注意选择合适的遍历顺序，以保证子问题的状态在计算当前节点状态时已经求解完毕。

总而言之，树形动态规划是一种针对树状结构问题的动态规划算法，通过拆解问题为子问题，并利用子问题的解求解更大规模的问题。它在解决树相关的问题时具有重要的应用价值。

树形DP例题

HDU-1520 Anniversary party

HDU-1520 Anniversary party

题目大意：

邀请员工参加party,但是为了避免员工和直属上司发生尴尬，规定员工和直属上司不能同时出席。

也就是每个人代表树中一个结点，每个结点拥有一个权值，相邻的父结点和子结点只能选择一个，问如何取才能使总权值之和最大。

员工编号从1到N。第一行输入包含数字N。1 < = N < = 6000。随后的N行中的每一行都包含相应员工的愉快度评级。欢乐评级是一个介于-128到127之间的整数。然后是描述主管关系树的T行。树规范的每一行都具有以下形式: L K 这意味着第K个员工是第L个员工的直接主管。输入以一行结束 0 0

解题思路：

根据DP的解题思路，定义状态为：

$dp[i][0]$，表示不选择当前结点时候的最优解

$dp[i][1]$，表示选择当前结点时候的最优解

其中状态转移方程分为下面两种情况：

1. 不选择当前结点，则子结点可选可不选，取其中的最大值即可，也就是$dp[u][0]+=max(dp[son][0],dp[son][1])$
2. 选择当前结点，则其子结点不能选，$dp[u][1]+=dp[son][0]$

AC代码：

#include
using namespace std;
const int maxn = 6010;
vector<int>tree[maxn];
int dp[maxn][2], father[maxn], value[maxn];
void dfs(int u) {
    dp[u][0] = 0; // 不参加party
    dp[u][1] = value[u]; // 参加party
    for(int i = 0; i < tree[u].size(); i++) {
        int son = tree[u][i];
        dfs(son); // 深搜子结点
        dp[u][0] += max(dp[son][0], dp[son][1]); // 父结点不选，子结点可选可不选
        dp[u][1] += dp[son][0]; // 父结点选择，子结点不能选
    }
}
int main() {
    int n, a, b;
    while(~scanf("%d", &n)) {
        for(int i = 1; i <= n; i++) {
            scanf("%d", &value[i]);
            tree[i].clear();
            father[i] = -1;
        }
        memset(dp, 0, sizeof(dp));
        while(true) { // 建树
            scanf("%d%d", &a, &b);
            if(a == 0 && b == 0) break;
            tree[b].push_back(a);
            father[a] = b; // 父子关系，表示a的父亲是b
        }
        for(int i = 1; i <= n; i++) {
            if(father[i] == -1) { // 寻找父结点，从父结点开始深搜
                dfs(i);
                printf("%d\n", max(dp[i][0], dp[i][1]));
                break;
            }
        }
    }
    return 0;
}

HDU-2196 Computer

HDU-2196 Computer

题目大意：

一颗树，根节点的编号是1，对其中的任意一个结点，求离这个结点最远结点的距离。

输入包含多个测试用例，每个用例的第一行是一个自然数N，N不超过10000，接下来N-1行，每行输入两个整数：第一个整数为某结点id，第二个整数为连接到这个结点需要的距离。

输出N行，表示距离第i个结点的最远距离

解题思路：

对于求解距离某结点的最长距离，应当分为两种情况：

对于任意一个结点

1. 结点 $i$ 的子树中的结点距离结点 $i$ 的最长距离，而为了方便第二种情况的计算，第一次深搜的时候需要记录结点 $i$ 的子树中某个结点到该结点的最长距离和第二长的距离。

2. 第二种情况就是结点 $i$ 往上走，而此时往上走又分为两种情况：

   从结点 $i$ 往上继续走，没有走结点 $i$ 的父结点到其子树的最长距离的路径

   若结点 $i$ 沿着其父结点的最长路径上走时，则需考虑结点 $i$ 是否在其父结点的最长子树上，此时则需要用到最初求得各个结点到其它结点的最长距离和次长距离，如果结点 $i$ 在其父结点的最长子树上那么 X = two + dist(i, i 的父结点)，否则 X = one + dist(i, i 的父结点)

综上所述，第一种情况和第二种情况求得两个值的最大值即为答案

状态的设计：结点 $i$ 的子树到 $i$ 的最长距离 $dp[i][0]$ 以及次长距离 $dp[i][1]$，从结点 $i$ 往上走的最长距离 $dp[i][2]$

#include
using namespace std;
struct Node {
    int id; // 子树结点编号
    int cost;
};
const int maxn = 10010;
int dp[maxn][3], n;
vector <Node> tree[maxn];
void init() { // 初始化和建树
    for(int i = 1; i <= n; i++) tree[i].clear();
    memset(dp, 0, sizeof(dp));
    int x, y;
    for(int i = 2; i <= n; i++) {
        scanf("%d%d", &x, &y);
        Node tmp;
        tmp.id = i;
        tmp.cost = y;
        tree[x].push_back(tmp);
    }
}
void dfs1(int father) { // 搜索以结点father为起点到子树的最长距离和次长距离
    int one = 0, two = 0; // one 记录father往下走的最长距离，two记录次长距离
    for(int i = 0; i < tree[father].size(); i++) { // 先处理子结点再处理父结点
        Node child = tree[father][i];
        dfs1(child.id); // 递归子结点，直到最底层
        int temp = child.cost + dp[child.id][0];
        if(temp >= one) {
            two = one;
            one = temp;
        }
        if(temp < one && temp > two) two = temp;
    }
    dp[father][0] = one; // 得到以father为起点的子树的最长距离
    dp[father][1] = two; // 得到以father为起点的子树的次长距离
}
void dfs2(int father) { // 先处理父结点再处理子结点
    for(int i = 0; i < tree[father].size(); i++) {
        Node child = tree[father][i];
        if(child.cost + dp[child.id][0] == dp[father][0]) // child在最长距离的子树上
            dp[child.id][2] = max(dp[father][1], dp[father][2]) + child.cost;
        else dp[child.id][2] = max(dp[father][0], dp[father][2]) + child.cost; //否则
        dfs2(child.id);
    }
}
int main() {
    while(~scanf("%d", &n)) {
        init();
        dfs1(1);
        dp[1][2] = 0;
        dfs2(1);
        for(int i = 1; i <= n; i++) {
            printf("%d\n", max(dp[i][0], dp[i][2]));
        }
    }
    return 0;
}

834. 树中距离之和

834. 树中距离之和

给定一个无向、连通的树。树中有 n 个标记为 0...n-1 的节点以及 n-1 条边 。

给定整数 n 和数组 edges ， edges[i] = [ai, bi]表示树中的节点 ai 和 bi 之间有一条边。

返回长度为 n 的数组 answer ，其中 answer[i] 是树中第 i 个节点与所有其他节点之间的距离之和。

示例 1:

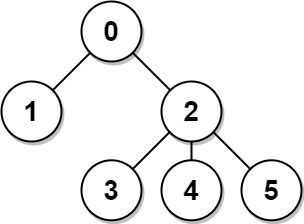
输入: n = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
输出: [8,12,6,10,10,10]
解释: 树如图所示。
我们可以计算出 dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5) 
也就是 1 + 1 + 2 + 2 + 2 = 8。 因此，answer[0] = 8，以此类推。

参考灵神的题解写出来的，不得不说灵神 yyds，比官方给出的题解简单多了。

灵神的题解地址：传送门

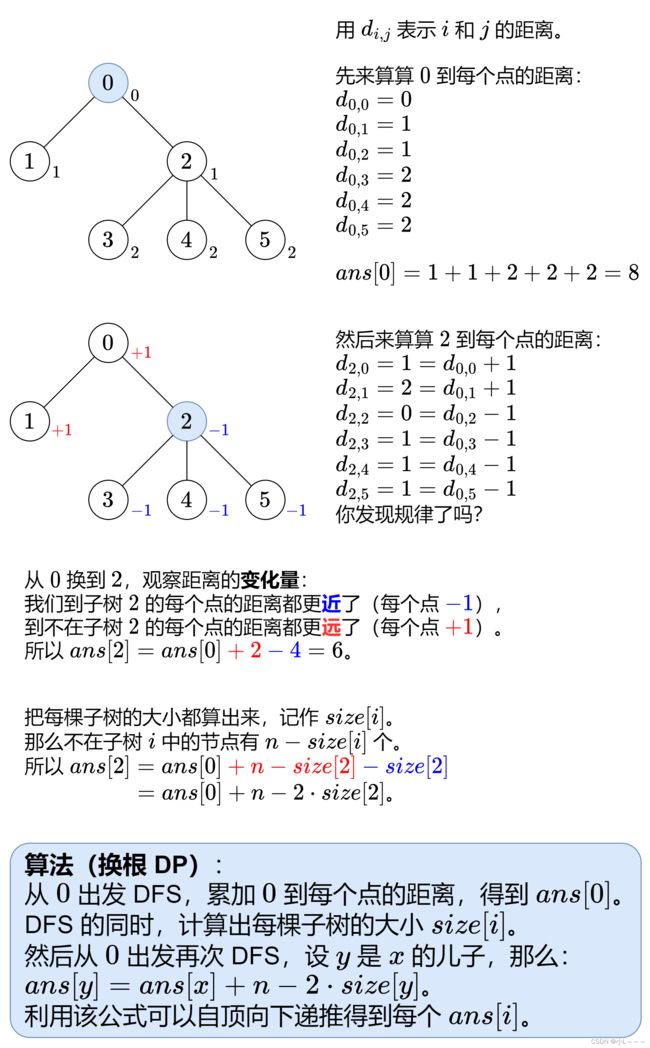
灵神给出的解题思路如下图所示：

AC代码：

class Solution {
public:
    static const int maxn = 3e4 + 10;
    vector<int>tree[maxn];
    vector<int> sumOfDistancesInTree(int n, vector<vector<int>>& edges) {
        for(auto edge : edges) {
            tree[edge[0]].push_back(edge[1]);
            tree[edge[1]].push_back(edge[0]);
        }
        vector<int>ans(n);
        vector<int>children(n, 1); // 每颗子树所包含结点数量
        function<void(int, int, int)> dfs1 = [&](int child, int father, int depth) {
            ans[0] += depth;
            for(auto i : tree[child]) {
                if(i != father) { // 避免访问父结点
                    dfs1(i, child, depth + 1);
                    children[child] += children[i]; // 累加子树大小
                }
            }
        };
        dfs1(0, -1, 0); // 0 没有父结点
        function<void(int, int)> dfs = [&](int child, int father) {
            for(auto i : tree[child]) {
                if(i != father) {
                    ans[i] += (ans[child] + n - children[i] * 2);
                    dfs(i, child);
                }
            }
        };
        dfs(0, -1);
        return ans;
    }
};