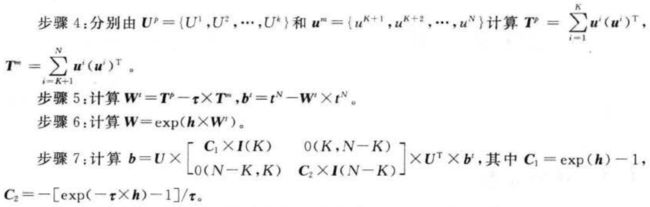离散 Hopfield 神经网络的分类与matlab实现

1 案例背景

1.1离散 Hopfield 神经网络学习规则

        离散型 Hopfield神经网络的结构、工作方式,稳定性等问题在第9章中已经进行了详细的介绍,此处不再赘述。本节将详细介绍离散Hopfield神经网络权系数矩阵的设计方法。设计权系数矩阵的目的是:
        ①保证系统在异步工作时的稳定性,即它的权值是对称的;

        ②保证所有要求记忆的稳定平衡点都能收敛到自己;
        ③使伪稳定点的数目尽可能地少;
        ④使稳定点的吸引力尽可能地大。
        常用的设计方法有:外积法和正交化法。

1.2高校科研能力评价概述

        科研能力是高校的核心能力,其高低已成为衡量一所高校综合实力的重要指标。科研能力的高低不仅影响高校自身的发展,对高校所在地区的经济发展也有很大的影响。如何准确评价高校的科研能力已成为摆在政府、企业和高校面前的一个十分重要的问题。影响科研能力的因素众多,且互相交叉,互相渗透和互相影响,无法用确定的数学模型进行描述。目前,高校科研能力评价的方法很多,但普遍存在工作繁琐、时间滞后等缺点,且人为主观因素对评价结果有很大的影响。如何快速,准确地对众多高校的科研能力进行客观、公正地评价?这是一个目前亟待解决的问题。

1.3问题描述

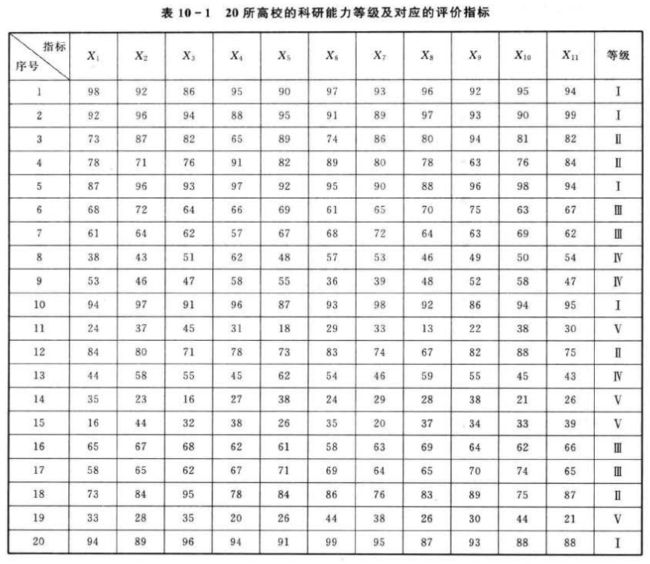
        影响高校科研能力的因素很多,本书仅以较为重要的11个影响因素作为评价指标:科研队伍(X1)、科研基地(X2),科技学识及其相应的载体(图书情报资料)(X3)、科研经费(X4)、科研管理(X5),信息接收加工能力(X6)、学识积累与技术储备能力(X7)、科研技术创新能力(X8)、知识释放能力(X9)、自适应调节能力(X10）、科学决策能力(X11)。

        高校科研能力一般分为五个等级:很强(Ⅰ)、较强(Ⅱ)、一般(Ⅲ)、较差(Ⅳ)及很差(V)。某机构对20所高校的科研能力进行了调研和评价,试根据调研结果中较为重要的11个评价指标的数据,并结合离散Hopfield神经网络的联想记忆能力,建立离散 Hopfield高校科研能力评价模型。

2模型建立

2.1设计思路

        将若干个典型的分类等级所对应的评价指标设计为离散型 Hopfield神经网络的平衡点，Hopfield神经网络学习过程即为典型的分类等级的评价指标逐渐趋近于 Hopfield神经网络的平衡点的过程。学习完成后,Hopfield神经网络储存的平衡点即为各个分类等级所对应的评价指标。当有待分类的高校的评价指标输人时,Hopfield神经网络即利用其联想记忆的能力逐渐趋近于某个储存的平衡点,当状态不再改变时,此时平衡点所对应的便是待求的分类等级。

2.2设计步骤

        在设计思路的基础上,本案例的设计步骤主要包括如下5个步骤,如图10-1所示。

        1. 设计理想的等级评价指标

        本书所研究的 20 所高校的科研能力等 11 个评价指标之间的关系如表 10 -1所 列。

        将各个等级的样本对应的各评价指标的平均值作为各个等级的理想评价指标,即作为Hopfield神经网络的平衡点,如表10-2所列。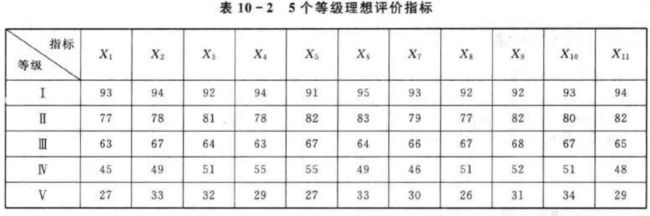

        2．理想的等级评价指标编码
        由于离散型Hopfield神经网络神经元的状态只有l和一l两种情况,所以将评价指标映射为神经元的状态时,需要将其进行编码。编码规则为:当大于或等于某个等级的指标值时，对应的神经元状态设为“1”,否则设为“一1”。理想的5个等级评价指标编码如图10-2所示.其中●表示神经元状态为“1”,即大于或等于对应等级的理想评价指标值,反之则用O表示。

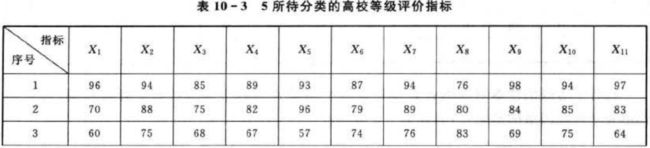
        3．待分类的等级评价指标编码
        5所待分类的高校等级评价指标如表10-3所列,根据上述的编码规则得到对应的编码，如图10-3所示。

         4．创建网络
        设计好理想的5个等级评价指标及编码后,即可利用MATLAB自带的神经网络工具箱函数创建离散型 Hopfield神经网络。
        5.仿真、分析
        网络创建完毕后,将待分类的5所高校等级评价指标的编码作为Hopfield神经网络的输人,经过一定次数的学习,便可以得到仿真结果。将仿真结果与真实的等级进行比较,可以对该模型进行合理的评价。

3 MATLAB 实现

        利用MATLAB神经网络工具箱提供的函数,将设计步骤在MATLAB环境下实现。

%% 离散Hopfield的分类——高校科研能力评价

%% 清空环境变量
clear all
clc

%% 导入数据
load class.mat

%% 目标向量
T = [class_1 class_2 class_3 class_4 class_5];

%% 创建网络
net = newhop(T);

%% 导入待分类样本
load sim.mat
A = {[sim_1 sim_2 sim_3 sim_4 sim_5]};

%% 网络仿真
Y = sim(net,{25 20},{},A);

%% 结果显示
Y1 = Y{20}(:,1:5)
Y2 = Y{20}(:,6:10)
Y3 = Y{20}(:,11:15)
Y4 = Y{20}(:,16:20)
Y5 = Y{20}(:,21:25)

%% 绘图
result = {T;A{1};Y{20}};
figure
for p = 1:3
    for k = 1:5 
        subplot(3,5,(p-1)*5+k)
        temp = result{p}(:,(k-1)*5+1:k*5);
        [m,n] = size(temp);
        for i = 1:m
            for j = 1:n
                if temp(i,j) > 0
                   plot(j,m-i,'ko','MarkerFaceColor','k');
                else
                   plot(j,m-i,'ko');
                end
                hold on
            end
        end
        axis([0 6 0 12])
        axis off
        if p == 1
           title(['class' num2str(k)])
        elseif p == 2
           title(['pre-sim' num2str(k)])
        else
           title(['sim' num2str(k)])
        end
    end                
end

% 案例扩展(无法分辨情况)
noisy = [1 -1 -1 -1 -1;-1 -1 -1 1 -1;
        -1 1 -1 -1 -1;-1 1 -1 -1 -1;
        1 -1 -1 -1 -1;-1 -1 1 -1 -1;
        -1 -1 -1 1 -1;-1 -1 -1 -1 1;
        -1 1 -1 -1 -1;-1 -1 -1 1 -1;
        -1 -1 1 -1 -1];
y = sim(net,{5 100},{},{noisy});
a = y{100}

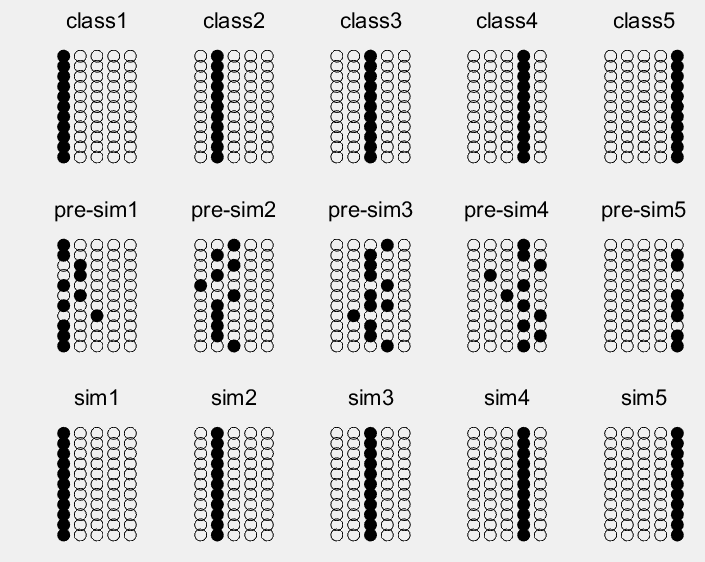
        仿真结果如图10-4所示。其中,第一行与图10-2相对应,表示5个理想的等级评价指标编码;第二行与图10-3相对应,表示5所待分类的高校等级评价指标编码;第三行为设计的 Hopfield神经网络分类的结果。从图中可以清晰地看出,设计的Hopfield网络可以有效地进行分类,从而可以对高校的科研能力进行客观公正地评价。

4案例扩展

        值得注意的是,本书中所设计的离散型 Hopfield神经网络并非适用于任何场合。当某所高校的优势与劣势并存且相当明显(即一些影响因素得分很高，一些影响因素得分很低)时，Hopfield神经网络将得不到确切的分类。:

% 案例扩展(无法分辨情况)
noisy = [1 -1 -1 -1 -1;-1 -1 -1 1 -1;
        -1 1 -1 -1 -1;-1 1 -1 -1 -1;
        1 -1 -1 -1 -1;-1 -1 1 -1 -1;
        -1 -1 -1 1 -1;-1 -1 -1 -1 1;
        -1 1 -1 -1 -1;-1 -1 -1 1 -1;
        -1 -1 1 -1 -1];
y = sim(net,{5 100},{},{noisy});
a = y{100}

        如图10-5所示,从仿真结果中可以看出,其不属于五种典型等级类别即意味着所设计的Hopfield神经网络寻找不到与之最为接近的平衡点,因此无法将其正确分类。在这一点上,和专家打分法的结果是一致的。

5.完整代码

https://download.csdn.net/download/weixin_44209907/88162199