树链剖分(轻重链)入门
写在前面
仅想学树剖LCA的同学其实不必要了解线段树
前置知识:树形结构,链式前向星(熟练),线段树(熟练),DFS序(熟练),LCA(了解定义)
树链剖分(树剖):将树分解为一条条不相交的,从祖先到孙子的链。
第零部分:建树与基本概念
建树:给定n个节点用链式前向星建树,这里不做过多赘述,值得一提的是要深入理解建树加边的过程。
基本概念:
1.重儿子:假设x有n个儿子节点,其中以3儿子节点的为根子树大小最大,3就是x的重儿子
2.轻儿子:除重儿子外的所有儿子均为轻儿子
以下图为例
1的重儿子为3,轻儿子为2
3的重儿子为6,其余的为轻儿子
3.轻边:x与轻儿子相连的边
4.重边:x与重儿子相连的边
5.轻链:均由轻儿子构成的一条链
6.重链:均由重儿子构成的一条链

第一部分:预处理节点信息
我们需要的信息如下
dep[X]:x节点的深度
fa[X]:x节点的父亲节点
son[X]:x节点的重儿子
siz[X]:x节点为根的子树大小
top[X]:x节点所在链的顶点
稍微有些晕?不要紧,接着往下看如何用两个DFS实现
首先第一个DFS我们直接获取dep[X],fa[X],son[X],siz[X]
void DFS1(int now,int fath)//传入当前节点和当前节点父亲节点编号{
fa[now]=fath;
siz[now]=1;son[now]=0;
dep[now]=dep[fath]+1;
for(int i=head[now];i;i=edge[i].nex){
if(edge[i].to==fath)
continue;
DFS1(edge[i].to,now);
siz[now]+=siz[edge[i].to];
if(siz[son[now]]<siz[edge[i].to]) //当now节点的重儿子不在是最大的,时候更新了
{
son[now]=edge[i].to;
}
}
}
接下来获取top[X]
我们处理的方式:优先对重儿子处理,重儿子处理结束后再处理轻儿子(新开链)
void DFS2(int now,int topx)//topx,先重儿子再轻儿子
{
top[now]=topx;
if(son[now]){
DFS2(son[now],topx);
}
else
return ;
for(int i=head[now];i;i=edge[i].nex)
{
if(edge[i].to!=fa[now]&&edge[i].to!=son[now])
{
DFS2(edge[i].to,edge[i].to);
}
}
}
看到这里,我们已经可以求解LCA问题了
实例:树剖LCA
OJ:P3379 【模板】最近公共祖先(LCA)
我们来看看预处理后树剖LCA的代码
int LCA(int x,int y){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])
swap(x,y);
x=fa[top[x]];
}
return dep[x]<dep[y]?x:y;
}
当我们把每个节点对应top记录好了之后,我们要获取两个节点的LCA完全可以通过让当前节点“跳跃”到当前节点所在链的顶端的父节点来实现(还记得我们剖分的不相交的链吗),每次选取当前两个节点中top的深度较大的来跳转。
AC代码 非压行
#include OK,学到这里如果要是只想学树剖LCA和普通的树上操作读者可以去找树上差分的文章,如果想要继续学习树剖的线段树维护可以继续阅读~
第二部分:树上操作
欢迎来到树链剖分最后的挑战:线段树优化树上操作
我们先分析一下第一部分,看看为什么要用线段树去优化(记着线段树的擅长区域:区间问题)。
第一部分分析:
首先,我们用DFS1获取了dep[X],fa[X],son[X],siz[X]
接着我们用DFS2获取了top[x]。我们来看看DFS2遍历数的过程:先重儿子,再轻儿子
先重儿子,再轻儿子,总是先遍历重儿子的话,一条重链上的遍历顺序是连续的!既然是连续的,那么一条重链就是一整个区间!
上图!
我们观察1 3 6 10这条链已然在新编节点中是1 2 3 4(区间)
观察以新编号为2的节点作为根的子树,里面是2 3 4 5 6(区间)
所以:一条重链和一个子树都恰好是一个区间
我们再来看一般性的情况:源节点从9到8,可以分为:9到2,2到1,8到3,3到1,四条链来进行操作
(圆圈内对应的原本节点的编号,蓝色数字对应的是DFS2遍历的顺序)
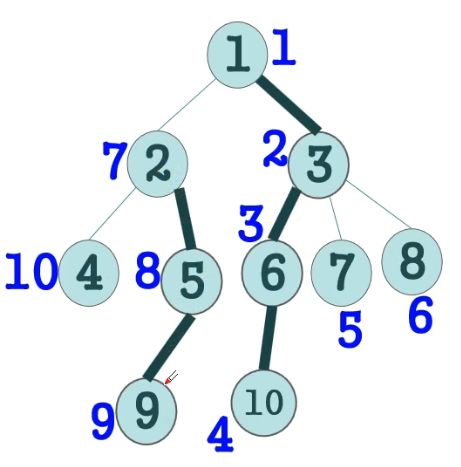
根据刚才的分析
1.我们需要在第一部分的DFS2加料,按照DFS2的DFS序来统计出新的节点编号和对应的新节点的权值
2.我们需要根据新的节点编号和新的权值来构造一颗线段树
3.借助我们存储的新节点编号把题目中给咱们的旧节点翻译成新节点来调用线段树。
我们来给DFS2加点东西
void DFS2(int now,int topx)//topx,先重儿子再轻儿子!!!!
{
top[now]=topx;
nid[now]=++cnt;//nid is new_id
nw[cnt]=w[now];//nw is new_weight
if(son[now])
DFS2(son[now],topx);
else
return ;
for(int i=head[now];i;i=edge[i].nex)
if(edge[i].to!=fa[now]&&edge[i].to!=son[now])
DFS2(edge[i].to,edge[i].to);
}
okk!我们记录好了新编节点和新编节点对应的重量了!
接下来,我们生成线段树!
void up(int p)
{
tree[p]=tree[ls]+tree[rs];
}
void down(int l,int r,int p)
{
tag[ls]+=tag[p];
tag[rs]+=tag[p];
tree[ls]+=(mid-l+1)*tag[p];
tree[ls]%=mod;
tree[rs]+=(r-mid)*tag[p];
tree[rs]%=mod;
tag[p]=0;
}
void bulid(int l,int r,int p)
{
if(l==r)
{
tree[p]=nw[l];
return ;
}
bulid(l,mid,ls);
bulid(mid+1,r,rs);
up(p);
}
void update(int l,int r,int nl,int nr,int p,int k)
{
if(l>=nl&&r<=nr)
{
tree[p]+=(r-l+1)*k;
tree[p]%=mod;
tag[p]+=k;
return ;
}
down(l,r,p);
if(mid>=nl)
{
update(l,mid,nl,nr,ls,k);
}
if(mid<nr)
{
update(mid+1,r,nl,nr,rs,k);
}
up(p);
}
long long query(int l,int r,int nl,int nr,int p)
{
if(l>=nl&&r<=nr)
{
return tree[p]%mod;
}
long long res=0ll;
down(l,r,p);
if(mid>=nl)
{
res+=query(l,mid,nl,nr,ls);
}
if(mid<nr)
{
res+=query(mid+1,r,nl,nr,rs);
}
return res;
}
最后一步,利用nid数组的翻译来调用线段树
记住这个模板哦!
void upd_Range(int x,int y,int k)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])
swap(x,y);
你的操作
x=fa[top[x]];
}
你的操作
}
调用!
long long q_Range(int x,int y)//询问一条路径
{
long long ans=0ll;
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])
swap(x,y);
ans=(ans+query(1,n,nid[top[x]],nid[x],1))%mod;
x=fa[top[x]];
}
if(dep[x]>dep[y])
swap(x,y);
ans=(ans+query(1,n,nid[x],nid[y],1))%mod;
return ans%mod;
}
long long q_Tree(int x)
{
return query(1,n,nid[x],nid[x]+siz[x]-1,1)%mod;
}
void upd_Range(int x,int y,int k)
{
k%=mod;
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])
swap(x,y);
update(1,n,nid[top[x]],nid[x],1,k);
x=fa[top[x]];
}
if(dep[x]>dep[y])
swap(x,y);
update(1,n,nid[x],nid[y],1,k);
}
void upd_Tree(int x,int k)
{
update(1,n,nid[x],nid[x]+siz[x]-1,1,k);
}
题目实例:P3384 【模板】轻重链剖分/树链剖分
ACcode
#include