【MATLAB第64期】基于MATLAB的无目标函数SOBOL等全局敏感性分析法模型合集(SOBOL,PAWN,GSA,GSUA,GSAT等) 【更新中】
【MATLAB第64期】基于MATLAB的无目标函数SOBOL等全局敏感性分析法模型合集(SOBOL,PAWN,GSA,GSUA,GSAT等) 【更新中】
引言
在前面几期,介绍了局部敏感性分析法,本期来介绍全局敏感性分析模型,因还在摸索中,所以更新较慢,敬请期待。
【MATLAB第31期】基于MATLAB的降维/全局敏感性分析/特征排序/数据处理回归问题MATLAB代码实现(持续更新)
【MATLAB第32期】【更新中】基于MATLAB的降维/全局敏感性分析/特征排序/数据处理分类问题MATLAB代码实现
【MATLAB第63期】基于MATLAB的改进敏感性分析方法IPCC,拥挤距离与皮尔逊系数法结合实现回归与分类预测
- 先介绍sobol有目标函数和无目标函数解决思路 。
- 后面会更新,通过遍历来筛选sobol样本数量,进行结果比对。
一、SOBOL(有目标函数)
(1)评价指标
评价指标包括:一阶影响指数S,总效应指数ST**
*一阶影响指数S:*显示由各个输入变量的方差产生的因变量的方差,根据一阶影响指数可以量化单个变量对模型的敏感程度
总效应指数ST:显示由每个输入变量的方差及其与其他输入变量的相互作用而产生的因变量的方差。
每个因变量和所有变量的 Sobol 指数都显示在专用的 Sobol 图中
,其中直方图按总效应指数ST排序。因变量对具有最高总效应指数ST的输入变量最敏感。
输入变量的总效应指数ST和一阶影响指数S之间的差异可以衡量该输入与其他输入变量之间相互作用的效果。
(2)运行思路
A、设定目标函数(3个变量,即维度D=3)
Y=X1^2+2*X2+X3-1
y=x(1)^2+2*x(2)+x(3)-1;
B、设定变量上下限
VarMin=[0 0 0];%各个参数下限
VarMax=[10 10 10];%各个参数上限
C、设定sobol其他参数
M=D*2 %2倍D数量的矩阵,提高样本丰富度
%则此时相当于共6个输入变量
VarMin=[0 0 0 0 0 0];%各个参数下限
VarMax=[10 10 10 10 10 10];%各个参数上限
nPop=4;%采样数量,样本数量(数量设置越大,准确率越高。为了方便展示数值,选取nPop=4)
D、生成sobol序列样本数据
这里要说,除了sobol序列函数可以生成样本数据,其他也可以, 比如正交设计、超立方抽样等等。很关键!!!举一反三即可
1、 生成多组N*M(即N行6列)的样本矩阵p。用自带函数sobolset生成。
p= sobolset(M)
**p 矩阵形式: 9007199254740992x6 sobolset**
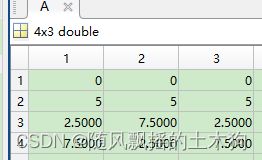
2、 筛选nPop*M(即4行6列)的样本矩阵R。
两种思路,第一种直接选取前nPop行的p采样数据 ,优点是方便快捷,但是缺点是样本不随机,并没有考虑上下限对样本的影响 。
% 第一种
R=p(1:nPop,:);%选取前nPop行
% 第二种
for i=1:nPop% 选取前nPop行被上下限空间处理后的样本
r=p(i,:);
r=VarMin+r.*(VarMax-VarMin);
R=[R; r];
end
本例因为最小和最大值一样,如果最小值和最大值均为0/1,则两种方法结果一致。
第二种方法R矩阵为:
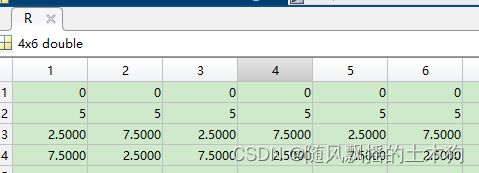
明显第二种方法更符合逻辑。
E、R样本拆分变换(提高样本丰富度)
1.将矩阵的前D列设置为矩阵A,后D列设置为B列,在我们的例子中就是矩阵m的前3列设置为矩阵A,后3列设置为矩阵B。
A=R(:,1:D);% 每行代表一组参数,其中每列代表每组参数的一个参数;行数就代表共有几组参数
B=R(:,D+1:end);
2.构造nPop*D的矩阵ABi(i = 1,2,…,D),即用矩阵B中的第i列替换矩阵A的第i列,以本体为例:
for i=1:D
tempA=A;
tempA(:,i)=B(:,i);
AB(1:nPop,1:D,i)=tempA;
end
经过这三步我们构造了A、B、AB1、AB2、AB3这五个矩阵,这样我们就有(D + 2) * nPop (即20)组x1、x2、x3输入数据,因此我们将有20组Y值。将上述的数据带入函数 ,这里详细的计算过程就不描述了。根据输入我们得出对应的Y值矩阵。
F、计算所有样本对应的Y值
for i=1:nPop
YA(i)=myfun(A(i,:)); %A矩阵对应的YA值
YB(i)=myfun(B(i,:));%B矩阵对应的YB值
for j=1:D
YAB(i,j)=myfun(AB(i,:,j));%YAB矩阵对应的YAB值
end
end
[YA YB YAB1 YAB2 YAB3 ]组合起来
依次各列数据代表YA YB YAB1 YAB2 YAB3值

G、一阶影响指数S值、总效应指数ST值计算
2.一阶影响指数S值
VarX=zeros(D,1);% S的分子
S=zeros(D,1);
VarY=var([YA;YB],1);% S的分母。 计算基于给定的样本总体的方差(EXCEL var.p())
for i=1:D
for j=1:nPop
VarX(i)=VarX(i)+YB(j)*(YAB(j,i)-YA(j));
end
VarX(i)=1/nPop*VarX(i);
S(i)=VarX(i)/VarY; %一阶影响指数
end
1.回到目标函数:y=x(1)^2+2*x(2)+x(3)-1;
可根据数学所学知识,得X1项为幂函数,X2项为系数=2的一次函数,X3项为系数=1的一次函数
根据常识即理论可知,敏感度排序X1>X2>X3
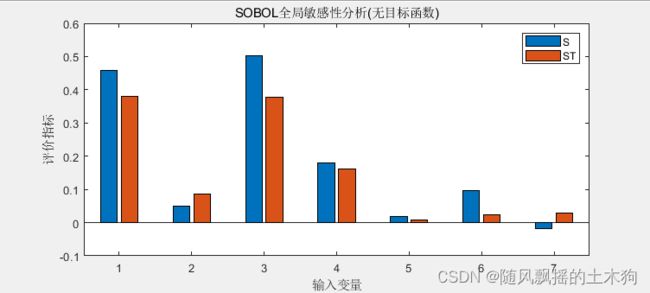
通过SOBOL的总效应指数ST柱状图结果也可以证实以上结论。
2.其次,一阶影响指数S中,第二个变量对应的S为负值,表示单个变量对因变量的敏感度,即所谓的局部敏感性分析法。
|X1|>|X2|>|X3|
而全局要考虑不同变量对因变量的影响,即ST定义——每个输入变量的方差及其与其他输入变量的相互作用而产生的因变量的方差。
3.输入变量的总效应指数ST和一阶影响指数S之间的差异可以衡量该输入与其他输入变量之间相互作用的效果。
二、SOBOL(无目标函数)
1.解决思路
(1)针对简单线性数据及非线性数据,用函数拟合得到公式,随后思路与上面一致。
(2)无法拟合得到公式, 即复杂非线性函数,需要通过借用机器学习模型,作为训练学习模型(黑箱子模型)
本文具体研究攻克第二种情况
有个前提(模型拟合性较好,对应数据较好)
即训练学习模型, 训练集和测试集拟合效果很棒。
如果拟合效果差,SOBOL分析结果一定存在较大误差。
2.模型选择
1.选用最基本的BP神经网络(不建议用BP,因为随机初始权值阈值,会让模型不够稳定),数据也为本人经常用的案例数据 ,103*8
2.前7列代表输入变量, 最后1列代表因变量。
3.选用模型后,几个点需要注意:
(1)数据固定,即训练样本/测试样本固定, 所代表的模型评价才够稳定。
(2)使用固定算子函数代码 ,即 rng default 或者rng(M)等 ,固定输出结果,保证运行结果一致。此一致并不代表永远一致, 只是代表此刻你打开的软件, 不关闭情况下每次运行一致。跟matlab版本有关,不同人运行结果也不一样。
(3)最为关键的一点 ,变量的上下限不能超过案例数据的上下限,为了保证模型的普适性和有效性!!!
比如案例数据的训练样本中, X1-X7的最小值为:
[137 0 0 160 4.4 708 650]
X1-X7的最大值为:
[374 193 260 240 19 1049.90 902]
那么你的sobol序列生成的数据也只能在这个范围,才能保证BP模型的有效性。
(4)生成样本的数量当然以多为好, 但不能跟案例数据样本数量差距太大。
(5)模型测试(不多说了,常规BP回归分析操作)


训练集数据的R2为:0.99981
测试集数据的R2为:0.97683
训练集数据的MAE为:0.066274
测试集数据的MAE为:0.83485
训练集数据的MBE为:0.018943
测试集数据的MBE为:0.81483
训练集和测试集R2如果均大于0.9还是可以的,评价指标好坏主观进行判定。
(6)保存模型所需要的变量
save bpnet net P_train P_test ps_output ps_input
通过sobol生成样本进行仿真预测。
3.SOBOL运行
4.SOBOL结果验证
此时还是有必要验证sobol的结果的。
最直观的就是对敏感性分析结果的结论进行验证:
根据上图,剔除S/ST较小的变量,使用BP一样的参数及样本(剔除后的),测试BP的效果。
看结果差异 ,如果差异不大,那么结果相对准确,如果差异大,那么sobol模型就有问题(模型为稳定模型,不建议用神经网络模型)。
此时,可以控制变量进行验证,如剔除X1/X2/X3/X4/X5/X6/X7其中一个变量,测试其他变量对因变量训练和测试结果。或者是剔除两个变量,或者剔除S/ST较小或者较大的变量进行测试等等。
一般情况下,剔除变量会造成结果变差。
因为BP不稳定,所以不对其进行验证,也不建议用BP进行训练学习。