对比Monte-Carlo与TD算法（Sarsa，Q-learning）【Code 3.附带MonteCarlo代码实现】

对比Monte-Carlo与TD算法（Sarsa，Q-learning）【Code 3.附带MonteCarlo代码实现】

This note records how the author begin to learn RL. Both theoretical understanding and code practice are presented. Many material are referenced such as ZhaoShiyu’s Mathematical Foundation of Reinforcement Learning.
This code refers to Mofan’s reinforcement learning course.

1. Monte-Carlo的由来

​ 为何出现了Monte-Carlo Method呢？这是因为在求解Bellman equation的过程中，
$$\begin{array}{rl}{v}_{\pi }(s)& =\mathbb{E}[G_t|S_t=s]\\ v_{\pi }(s)& =\sum _a\pi (a|s)[\sum _{r}p(r|s,a)r+\sum _{s^{\prime }}p(s^{\prime }|s,a)v_{\pi }(s^{\prime })]\text{(Bellman equation of state value)}\\ q_{\pi }(s,a)& =\mathbb{E}[G_t|S_t=s,A_t=a]\\ q_{\pi }(s,a)& =\sum _{r}p(r|s,a)r+\sum _{s^{\prime }}p(s^{\prime }|s,a)v_{\pi }(s^{\prime })\text{(Bellman equation of action value)}\end{array}$$
若不知道Markov decision process的模型$p(r|s,a),p(s^{\prime }|s,a)$，我们将难以求解，因此我们从Bellman expectaion equation出发，$q_{\pi }(s,a)=\mathbb{E}[G_t|S_t=s,A_t=a]$表示从状态$s$出发采取动作$a$的回报$G_t$的平均值，其中$G_t$是一个随机变量，我们根据大数定律(Law of large number)可知
$$q_{\pi }(s,a)=\mathbb{E}[G_t|S_t=s,A_t=a]\approx \frac{1}{n}\sum _{i=1}^n{g}_{\pi }^{(i)}(s,a)$$
我们可以用从状态$s$采取动作$a$出发的一系列episodes的回报（return）的平均值来逼近这个真值，根据大数定律，当这样的采样越多的时候逼近值越接近真值。若这样是可行的，那么我们求解Bellman equation的时候就不再需要Markov decision process的模型了，这种方式就被称作 model-free。

​ 大数定律给我提供了理论支持，我们即可以将上式理解为求解$g(q_{\pi }(s,a))=q_{\pi }(s,a)-\mathbb{E}[G_t|S_t=s,A_t=a]$的零点，根据Robbins-Monro算法（详见：Chapter 6. Stochastic Approximation），我们可以获得带噪声的观测

$$\begin{array}{rl}\tilde{g}(q_{\pi }(s,a),\eta )& =q_{\pi }(s,a)-g(s,a)\\ & =\underset{g(q_{\pi }(s,a))}{q_{\pi }(s,a)-\mathbb{E}[G_t|S_t=s,A_t=a]}+\underset{\eta }{\mathbb{E}[G_t|S_t=s,A_t=a]-g(s,a)}\end{array}$$

那么我们可以得到求解$q_{\pi }(s,a)$的增量式算法

$$\text{MC-Basic}:\{\begin{array}{rl}{q}_{t+1}(s_t,a_t)& =q_t(s_t,a_t)-{\alpha }_t(s_t,a_t)[q_t(s_t,a_t)-g_t(s_t,a_t)]\\ q_{t+1}(s,a)& =q_t(s,a),\text{for all }(s,a)\ne (s_t,a_t)\end{array}$$

其中${\alpha }_t(s_t,a_t)$是系数，虽然写法是增量式的，但是算法的执行并不是增量式的，因为我们必须等一个完整的episode执行完毕之后，才能得到回报$g_t(s_t,a_t)$

$$g_t(s_t,a_t)=r_{t+1}+\gamma r_{t+2}+{\gamma }^2{r}_{t+3}+\cdots$$

所以，补全上述的MC算法

$$\text{MC-Basic}:\{\begin{array}{rl}{q}_{t+1}(s_t,a_t)& =q_t(s_t,a_t)-{\alpha }_t(s_t,a_t)[q_t(s_t,a_t)-g_t(s_t,a_t)]\\ g_t(s_t,a_t)& =r_{t+1}+\gamma r_{t+2}+{\gamma }^2{r}_{t+3}+\cdots \\ q_{t+1}(s,a)& =q_t(s,a),\text{for all }(s,a)\ne (s_t,a_t)\end{array}$$

2. TD算法Sarsa的由来

​ TD算法全称为temporal-difference algorithm，顾名思义TD算法是真正意义上的增量式算法，其中Sarsa是怎么得到的呢？将Monte-Carlo中求解的Bellman expectation equation改写成
$$\begin{array}{rl}{q}_{\pi }(s,a)& =\mathbb{E}[G_t|S_t=s,A_t=a]\\ q_{\pi }(s,a)& =\mathbb{E}[R+\gamma q_{\pi }(S^{\prime },A^{\prime })|S_t=s,A_t=a]\end{array}$$
同样使用Robbins-Monro算法来求解下式的零点
g ( q π ( s , a ) ) ≜ q π ( s , a ) − E [ R + γ q π ( S ′ , A ′ ) ∣ S = s , A = a ] g(q_\pi(s,a)) \triangleq q_\pi(s,a) - \mathbb{E}{\Big[ R + \gamma q_\pi(S^\prime,A^\prime) \Big| S=s, A=a\Big]} g(qπ​(s,a))≜qπ​(s,a)−E[R+γqπ​(S′,A′) ​S=s,A=a]
则获得带噪声的观测值
g ~ ( q π ( s , a ) , η ) = q π ( s , a ) − [ r + γ q π ( s ′ , a ′ ) ] = q π ( s , a ) − E [ R + γ q π ( S ′ , A ′ ) ∣ S = s , A = a ] ⏟ g ( q π ( s , a ) ) + [ E [ R + γ q π ( S ′ , A ′ ) ∣ S = s , A = a ] − [ r + γ q π ( s ′ , a ′ ) ] ] ⏟ η \begin{aligned} \tilde{g}\Big(q_\pi(s,a),\eta \Big) & = q_\pi(s,a) - \Big[r+\gamma q_\pi(s^\prime,a^\prime) \Big] \\ & = \underbrace{q_\pi(s,a) - \mathbb{E}{\Big[ R + \gamma q_\pi(S^\prime,A^\prime)\Big| S=s, A=a\Big]}}_{g(q_\pi(s,a))} + \underbrace{\Bigg[\mathbb{E}{\Big[ R + \gamma q_\pi(S^\prime,A^\prime) \Big| S=s, A=a\Big]} - \Big[r+\gamma q_\pi(s^\prime,a^\prime)\Big] \Bigg]}_{\eta} \end{aligned} g~​(qπ​(s,a),η)​=qπ​(s,a)−[r+γqπ​(s′,a′)]=g(qπ​(s,a)) qπ​(s,a)−E[R+γqπ​(S′,A′) ​S=s,A=a]​​+η [E[R+γqπ​(S′,A′) ​S=s,A=a]−[r+γqπ​(s′,a′)]]​​​
然后使用Robbins-Monro算法可以得到下列迭代式
$$q_{k+1}(s,a)=q_k(s,a)-{\alpha }_k[q_k(s,a)-(r_k+\gamma q_k(s_k^{\prime },a_k^{\prime })\left)\right]$$
我们将采样值$(s,a,r_k,s_k^{\prime },a_k^{\prime })$改写成$(s_t,a_t,r_{t+1},s_{t+1},a_{t+1})$则获得了真正意义上的时序差分Sarsa算法

$$\text{Sarsa}:\{\begin{array}{rl}{q}_{t+1}(s_t,a_t)& =q_t(s_t,a_t)-{\alpha }_t(s_t,a_t)[q_t(s_t,a_t)-(r_{t+1}+\gamma q_t(s_{t+1},a_{t+1}))]\\ q_{t+1}(s,a)& =q_t(s,a),\text{for all }(s,a)\ne (s_t,a_t)\end{array}$$

3 TD算法Q-learning 的由来

​ Monte-Carlo和Sarsa求解的是不同形式的Bellman expectation equation，但是Q-learning求解的是Bellman expectation optimality equation，就是我们常说的贝尔曼期望最优等式。
$$q(s,a)=\mathbb{E}[R+\gamma \underset{a\in \mathcal{A}(s)}{\max }q(S^{\prime },a)|S=s,A=a],\text{ for all }s,a\text{(expectation form)}$$
类似于上述两种的推导方式，这里不再详细阐述
$$g(q(s,a))\triangleq q(s,a)-\mathbb{E}[R+\gamma \underset{a\in \mathcal{A}(S^{\prime })}{\max }q(S^{\prime },a)|S=s,A=a]$$
带噪声的观测：
$$\begin{array}{rl}\tilde{g}(q(s,a))& =q(s,a)-[r+\gamma \underset{a\in \mathcal{A}(s^{\prime })}{\max }q(s^{\prime },a)]\\ & =\underset{g(q(s,a))}{q(s,a)-\mathbb{E}[R+\gamma \underset{a\in \mathcal{A}(S^{\prime })}{\max }q(S^{\prime },a)|S=s,A=a]}+\underset{\eta }{\mathbb{E}[R+\gamma \underset{a\in \mathcal{A}(S^{\prime })}{\max }q(S^{\prime },a)|S=s,A=a]-[r+\gamma \underset{a\in \mathcal{A}(s^{\prime })}{\max }q(s^{\prime },a)]}\end{array}$$
应用Robbins-Monro算法
$$q_{k+1}(s,a)=q_k(s,a)-{\alpha }_k(s,a)[q_k(s,a)-(r_k+\gamma \underset{a\in \mathcal{A}(s^{\prime })}{\max }{q}_k(s^{\prime },a)\left)\right]$$
将$(s,a,r_k,s_k^{\prime })$替换成$(s_t,a_t,r_{t+1},s_{t+1})$，则有
$$\text{Q-learning}:\{\begin{array}{rl}{q}_{t+1}(s_t,a_t)& =q_t(s_t,a_t)-{\alpha }_t(s_t,a_t)[q_t(s_t,a_t)-(r_{t+1}+\gamma \underset{a\in \mathcal{A}(s_{t+1})}{\max }{q}_t(s_{t+1},a))]\\ q_{t+1}(s,a)& =q_t(s,a),\text{for all }(s,a)\ne (s_t,a_t)\end{array}$$

4. Summary

​ 我们将对比TD target等指标，若不清楚的可以（详见： Chapter 7. Temporal Difference Learning）

5. Code

maze_env_custom.py主要用于构建强化学习中智能体的交互环境

import numpy as np
import time
import sys
import tkinter as tk
# if sys.version_info.major == 2: # 检查python版本是否是python2
#     import Tkinter as tk
# else:
#     import tkinter as tk


UNIT = 40   # pixels
MAZE_H = 4  # grid height
MAZE_W = 4  # grid width


class Maze(tk.Tk, object):
    def __init__(self):
        super(Maze, self).__init__()
        # Action Space
        self.action_space = ['up', 'down', 'right', 'left'] # action space 
        self.n_actions = len(self.action_space)

        # 绘制GUI
        self.title('Maze env')
        self.geometry('{0}x{1}'.format(MAZE_W * UNIT, MAZE_H * UNIT))   # 指定窗口大小 "width x height"
        self._build_maze()

    def _build_maze(self):
        self.canvas = tk.Canvas(self, bg='white',
                           height=MAZE_H * UNIT,
                           width=MAZE_W * UNIT)     # 创建背景画布

        # create grids
        for c in range(UNIT, MAZE_W * UNIT, UNIT): # 绘制列分隔线
            x0, y0, x1, y1 = c, 0, c, MAZE_H * UNIT
            self.canvas.create_line(x0, y0, x1, y1)
        for r in range(UNIT, MAZE_H * UNIT, UNIT): # 绘制行分隔线
            x0, y0, x1, y1 = 0, r, MAZE_W * UNIT, r
            self.canvas.create_line(x0, y0, x1, y1)

        # create origin 第一个方格的中心，
        origin = np.array([UNIT/2, UNIT/2]) 

        # hell1
        hell1_center = origin + np.array([UNIT * 2, UNIT])
        self.hell1 = self.canvas.create_rectangle(
            hell1_center[0] - (UNIT/2 - 5), hell1_center[1] - (UNIT/2 - 5),
            hell1_center[0] + (UNIT/2 - 5), hell1_center[1] + (UNIT/2 - 5),
            fill='black')
        # hell2
        hell2_center = origin + np.array([UNIT, UNIT * 2])
        self.hell2 = self.canvas.create_rectangle(
            hell2_center[0] - (UNIT/2 - 5), hell2_center[1] - (UNIT/2 - 5),
            hell2_center[0] + (UNIT/2 - 5), hell2_center[1] + (UNIT/2 - 5),
            fill='black')

        # create oval 绘制终点圆形
        oval_center = origin + np.array([UNIT*2, UNIT*2])
        self.oval = self.canvas.create_oval(
            oval_center[0] - (UNIT/2 - 5), oval_center[1] - (UNIT/2 - 5),
            oval_center[0] + (UNIT/2 - 5), oval_center[1] + (UNIT/2 - 5),
            fill='yellow')

        # create red rect 绘制agent红色方块,初始在方格左上角
        self.rect = self.canvas.create_rectangle(
            origin[0] - (UNIT/2 - 5), origin[1] - (UNIT/2 - 5),
            origin[0] + (UNIT/2 - 5), origin[1] + (UNIT/2 - 5),
            fill='red')

        # pack all 显示所有canvas
        self.canvas.pack()


    def get_state(self, rect):
            # convert the coordinate observation to state tuple
            # use the uniformed center as the state such as 
            # |(1,1)|(2,1)|(3,1)|...
            # |(1,2)|(2,2)|(3,2)|...
            # |(1,3)|(2,3)|(3,3)|...
            # |....
            x0,y0,x1,y1 = self.canvas.coords(rect)
            x_center = (x0+x1)/2
            y_center = (y0+y1)/2
            state = (int((x_center-(UNIT/2))/UNIT + 1), int((y_center-(UNIT/2))/UNIT + 1))
            return state


    def reset(self):
        self.update()
        self.after(500) # delay 500ms

        # print("\nCurrent objects on canvas:", self.canvas.find_all())  # 查看画布上的所有对象
        # if self.rect is not None:
        #     self.canvas.delete(self.rect)   # delete origin rectangle
        # else:
        #     print("self.rect is None. Cannot delete.")

        self.canvas.delete(self.rect)   # delete origin rectangle
        origin = np.array([UNIT/2, UNIT/2])
        self.rect = self.canvas.create_rectangle(
            origin[0] - (UNIT/2 - 5), origin[1] - (UNIT/2 - 5),
            origin[0] + (UNIT/2 - 5), origin[1] + (UNIT/2 - 5),
            fill='red')
        # return observation 
        return self.get_state(self.rect)   

    

    def step(self, action):
        # agent和环境进行一次交互
        s = self.get_state(self.rect)   # 获得智能体的坐标
        base_action = np.array([0, 0])
        reach_boundary = False
        if action == self.action_space[0]:   # up
            if s[1] > 1:
                base_action[1] -= UNIT
            else: # 触碰到边界reward=-1并停留在原地
                reach_boundary = True

        elif action == self.action_space[1]:   # down
            if s[1] < MAZE_H:
                base_action[1] += UNIT
            else:
                reach_boundary = True   

        elif action == self.action_space[2]:   # right
            if s[0] < MAZE_W:
                base_action[0] += UNIT
            else:
                reach_boundary = True

        elif action == self.action_space[3]:   # left
            if s[0] > 1:
                base_action[0] -= UNIT
            else:
                reach_boundary = True

        self.canvas.move(self.rect, base_action[0], base_action[1])  # move agent

        s_ = self.get_state(self.rect)  # next state

        # reward function
        if s_ == self.get_state(self.oval):     # reach the terminal
            reward = 1
            done = True
            s_ = 'success'
        elif s_ == self.get_state(self.hell1): # reach the block
            reward = -1
            s_ = 'block_1'
            done = False
        elif s_ == self.get_state(self.hell2):
            reward = -1
            s_ = 'block_2'
            done = False
        else:
            reward = 0
            done = False
            if reach_boundary:
                reward = -1

        return s_, reward, done

    def render(self):
        time.sleep(0.15)
        self.update()




if __name__ == '__main__':
    def test():
        for t in range(10):
            s = env.reset()
            print(s)
            while True:
                env.render()
                a = 'right'
                s, r, done = env.step(a)
                print(s)
                if done:
                    break
    env = Maze()
    env.after(100, test)      # 在延迟100ms后调用函数test
    env.mainloop()

RL_brain.py 主要用于实现强化学习的更新算法，这里使用的是Monte-Carlo $ϵ$-greedy 算法，使用first visit策略
如图所示

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt


class RL():
    def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9):
        self.actions = actions  # action list
        self.lr = learning_rate
        self.gamma = reward_decay
        self.epsilon = e_greedy # epsilon greedy update policy
        self.q_table = pd.DataFrame(columns=self.actions, dtype=np.float64)
        # 维护访问的state-action pair and return
        self.reward_sa_pair = []
        self.reward_list = []
        # 维护保存每个episode return的列表
        self.return_list = []

    def check_state_exist(self, state):
        # check if there exists the state
        if str(state) not in self.q_table.index:
            self.q_table = pd.concat(
                [
                self.q_table,
                pd.DataFrame(
                        data=np.zeros((1,len(self.actions))),
                        columns = self.q_table.columns,
                        index = [str(state)]
                    )
                ]
            )


    def choose_action(self, observation):
        """
            Use the epsilon-greedy method to update policy
        """
        self.check_state_exist(observation)
        # action selection
            # epsilon greedy algorithm
        if np.random.uniform() < self.epsilon:
            
            state_action = self.q_table.loc[observation, :]
            # some actions may have the same value, randomly choose on in these actions
            # state_action == np.max(state_action) generate bool mask
            # choose best action
            action = np.random.choice(state_action[state_action == np.max(state_action)].index)
        else:
            # choose random action
            action = np.random.choice(self.actions)
        return action

    def write_sa_r(self, s, a, r):
        # 写入state-action pair 和 reward
        self.reward_sa_pair.append((s,a))
        self.reward_list.append(r)
    
    def _calculate_return(self, s, a):
        # 计算从 state action pair (s,a) 出发的return 采用first visit策略
        ret = 0
        sa_index = self.reward_sa_pair.index((s,a))
        for i in range(sa_index, len(self.reward_sa_pair)):
            ret = ret * self.gamma + self.reward_list[i]
        return ret
    
    def calculate_episode_return(self):
        (s,a) = self.reward_sa_pair[0]
        self.return_list.append(self._calculate_return(s, a))


    def show_q_table(self):
        print()
        print(self.q_table)
    
    def plot_episode_return(self, name):
        # plot
        episodes_list = list(range(len(self.return_list)))
        plt.plot(episodes_list, self.return_list)
        plt.xlabel('Episodes')
        plt.ylabel('Returns')
        plt.title('{} on {}'.format(name,'Maze Walking'))
        plt.show()


class MonteCarloTable(RL):
    def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9):
        super(MonteCarloTable, self).__init__(actions, learning_rate, reward_decay, e_greedy)
        
    def learn(self):
        # show info
        # print(self.reward_sa_pair)
        # print(self.reward_list)
        # self.show_q_table()

        for (s,a) in self.reward_sa_pair:
            self.check_state_exist(s)
            q_predict = self.q_table.loc[str(s), a]
            q_target = self._calculate_return(s, a)
            self.q_table.loc[str(s),a] += self.lr * (q_target - q_predict)
        # clear
        self.reward_list = []
        self.reward_sa_pair = []

main.py是运行的主函数

from maze_env_custom import Maze
from RL_brain import MonteCarloTable
from tqdm import tqdm


MAX_EPISODE = 100
Batch_Size = 10
num_iteration = int(MAX_EPISODE / Batch_Size)

def update():
    for i in range(num_iteration):
        with tqdm(total=(MAX_EPISODE/num_iteration), desc="Iteration %d"%(i+1)) as pbar:


            for i_episode in range(int(MAX_EPISODE/num_iteration)):

                # initial observation, observation is the rect's coordiante
                # observation is [x0,y0, x1,y1]
                observation = env.reset()  
                done = False
                while not done:
                    # fresh env
                    env.render()

                    # RL choose action based on observation ['up', 'down', 'right', 'left']
                    action = RL.choose_action(str(observation))

                    # RL take action and get next observation and reward
                    observation_, reward, done = env.step(action)
                    
                    RL.write_sa_r(observation, action, reward)


                    # swap observation
                    observation = observation_

                # calculate the return of this episode
                RL.calculate_episode_return()

                # after one episode update the q_value
                RL.learn()


                if (i_episode+1) % num_iteration == 0:
                    pbar.set_postfix({
                        "episode": "%d"%(MAX_EPISODE/num_iteration*i + i_episode+1)
                    })
                # update the tqdm
                pbar.update(1)
                
                # show q_table
                print(RL.q_table)
                print('\n')


    # end of game
    print('game over')
    # destroy the maze_env
    env.destroy()

    RL.plot_episode_return('Monte_Carlo')

    



if __name__ == "__main__":
    env = Maze()
    RL = MonteCarloTable(env.action_space)
    
    #指定env演示100ms后执行update函数
    env.after(100, update)
    env.mainloop()

最终获得的Q table如下

              up      down     right      left
(1, 1)  -2.564431  0.328240 -2.384846 -0.616915
(2, 1)  -0.035416  0.063559 -0.031118 -2.470048
(2, 2)   0.070173 -0.117370 -0.037543 -0.030519
block_1 -0.020951  0.077255  0.000000  0.001000
(1, 2)  -0.145853  0.435657 -0.181815 -0.108147
(1, 3)  -0.037165  0.465386 -0.076265 -1.942067
block_2  0.000000  0.000000  0.182093 -0.133333
(3, 1)  -0.062227  0.002970 -0.034015 -0.000105
(4, 1)  -0.199058 -0.006290 -0.011604  0.000000
(4, 2)   0.000000 -0.006290  0.000000  0.002970
(4, 3)   0.002970  0.000000 -0.006290  0.000000
(1, 4)   0.013556 -0.030012  0.485312  0.007172
(2, 4)   0.000000 -0.008719  0.499194  0.000000
(3, 4)   0.515009  0.001990  0.001990  0.000000
(4, 4)   0.001990  0.000000  0.000000  0.000000

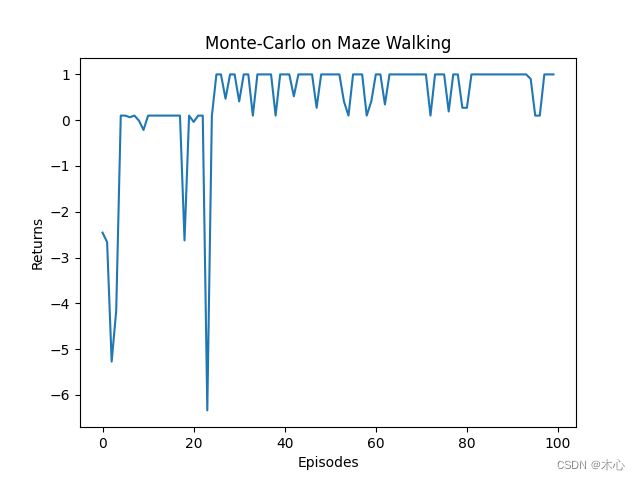
回报（return）的变化曲线如下：

---

Reference

赵世钰老师的课程
莫烦ReinforcementLearning course
Chapter 6. Stochastic Approximation
Chapter 7. Temporal Difference Learning