Python---Numpy
文章目录
- 1.Numpy是什么?
- 2.ndarray
-
-
- 2.1 什么是ndarray?
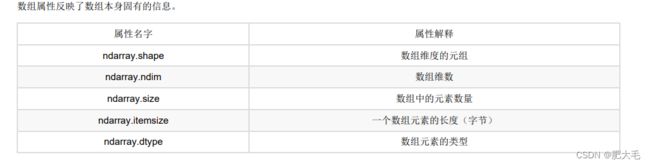
- 2.2 ndarray的属性
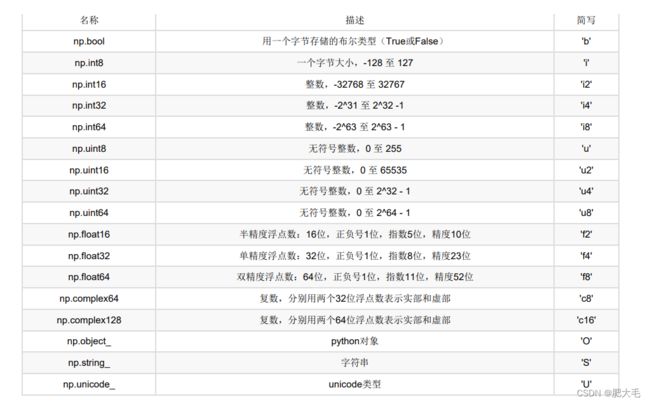
- 2.3 ndarray的类型
-
- 3.Numpy基本操作
-
-
- 3.1 生成0或1的数组
- 3.2 从现有数组生成数组
-
-
- 拓展:浅拷贝和深拷贝
-
- 3.3 生成固定范围的数组
- 3.4 生成随机数组
-
-
- 3.4.1 正态分布
- 3.4.2 均匀分布
-
- 3.5 形状修改
- 3.6 类型修改
- 3.7 数组的去重
- 3.8 数组的索引以及切片
-
- 4.ndarray运算
-
-
- 4.1 逻辑运算
-
-
- 通用判断函数
-
- 4.2 统计运算
-
1.Numpy是什么?
NumPy(Numerical Python)是一个强大的Python数值计算库。它提供对大型多维数组和矩阵的支持,并提供了许多高效操作这些数组的数学函数。 NumPy是Python科学计算的基础库,在诸如机器学习、数据科学、工程学和研究等领域得到广泛应用。

要使用NumPy,首先需要安装它。可以使用pip安装它:
pip install numpy
Numpy支持常见的数组和矩阵操作。对于同样的数值计算任务,使用Numpy比直接使用Python要简洁的多。
2.ndarray
2.1 什么是ndarray?
NumPy提供了一个N维数组类型ndarray,它描述了相同类型的“items”的集合。
ndarray(N维数组)是NumPy库中最重要的数据结构之一。它是一个多维、同类型数据的容器,可以存储在内存中的连续块,提供了许多功能和操作来高效地处理大规模数值数据。
机器学习的最大特点就是大量的数据运算,那么如果没有一个快速的解决方案,那可能现在python也在机器学习领域达不到好的效果。
Numpy专门针对ndarray的操作和运算进行了设计,所以数组的存储效率和输入输出性能远优于Python中的嵌套列表,数组越大,Numpy的优势就越明显。
ndarray到底跟原生python列表有什么不同呢,请看一张图:
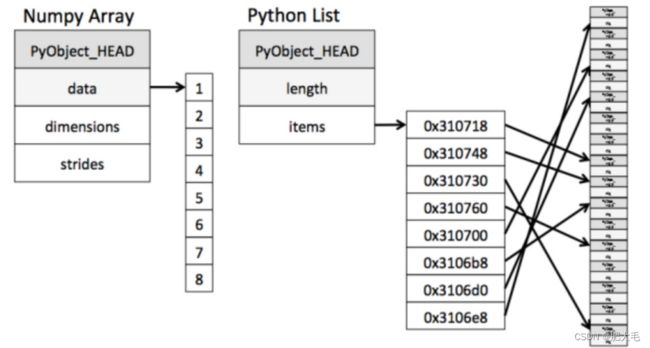
从图中我们可以看出ndarray在存储数据的时候,数据与数据的地址都是连续的,这样就给使得批量操作数组元素时速度更快。
这是因为ndarray中的所有元素的类型都是相同的,而Python列表中的元素类型是任意的,所以ndarray在存储元素时内存可以连续,而python
原生list就只能通过寻址方式找到下一个元素,这虽然也导致了在通用性能方面Numpy的ndarray不及Python原生list,但在科学计算中,Numpy
的ndarray就可以省掉很多循环语句,代码使用方面比Python原生list简单的多。此外ndarray支持并行化运算(向量化运算)。
使用numpy生成一个数组
import numpy as np
#使用numpy生成一个数组
a=np.array([1,2,3,4,5,6])
a
2.2 ndarray的属性
2.3 ndarray的类型
import numpy as np
# 创建不同形状的数组
# 二维数组
a=np.array([[1,2,3],[4,5,6]],dtype=int)
# 一维数组
b=np.array([1,2,3,4,5],dtype=int)
# 三维数组
c=np.array([[[1,2,3],[4,5,6]],[[2,7,8],[3,6,9]]],dtype=int)
# 打印数组的形状
a.shape
b.shape
c.shape
3.Numpy基本操作
3.1 生成0或1的数组
import numpy as np
#生成全是1的数组
np.ones([4,8])
ones
#生成全是0的数组
zeros=np.zeros([4,8])
zeros
3.2 从现有数组生成数组

当创建新的数组时,numpy.array() 默认会复制数据,以确保创建的数组与原始数据没有共享内存。这是所谓的“拷贝”操作。
numpy.asarray() 不会执行拷贝操作,而只是将该数组返回,这有助于节省内存和提高性能。
import numpy as np
a = np.array([[1,2,3],[4,5,6]])
# 从现有的数组当中创建
a1 = np.array(a)
# 相当于索引的形式,并没有真正的创建一个新的
a2 = np.asarray(a)
拓展:浅拷贝和深拷贝
**浅拷贝是创建一个新的数据结构,并复制原始数据结构中的元素。**如果原始数据结构是一个单层结构(没有嵌套的对象),那么浅拷贝将复制所有元素。但是,如果原始数据结构中有嵌套的对象(如列表中嵌套了另一个列表,或字典中嵌套了另一个字典),浅拷贝将不会递归复制嵌套对象,而是复制它们的引用。
深拷贝是创建一个新的数据结构,并递归复制原始数据结构中的所有元素,包括嵌套对象。 这意味着原始数据结构中的每个元素及其嵌套的元素都将在新数据结构中独立存在,不共享引用。
3.3 生成固定范围的数组
np.linspace (start, stop, num, endpoint)
创建等差数组 — 指定数量
参数:
start:序列的起始值
stop:序列的终止值
num:要生成的等间隔样例数量,默认为50
endpoint:序列中是否包含stop值,默认为ture
np.linspace(0,100,11)
np.arange(start,stop, step, dtype)
创建等差数组 — 指定步长
参数 step:步长,默认值为1
np.arange(40,50,1)
![]()
np.logspace(start,stop, num)
创建等比数列
参数:
num:要生成的等比数列数量,默认为50
logspace(1, 3, 5) 返回一个包含 5 个均匀分布在对数刻度上的数据点的数组。这些数据点分别是 101,101.5,102,102.5 和 10^3。
3.4 生成随机数组
3.4.1 正态分布
正态分布是一种概率分布。正态分布是具有两个参数μ和σ的连续型随机变量的分布,第一参数μ是服从正态分布的随机变量的均值,第二个参数σ是此随机变量的标准差,所以正态分布记作N(μ,σ )。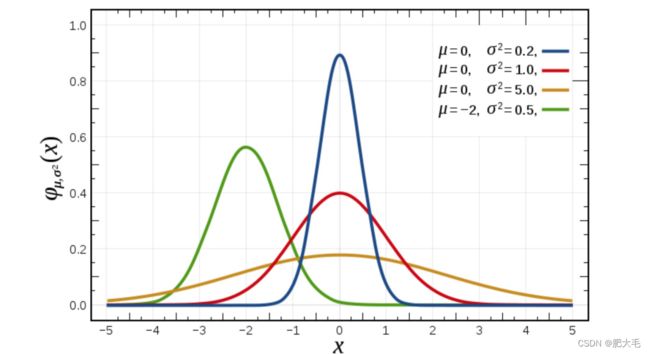
μ决定了其位置,其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。
正态分布的创建:
np.random.randn(d0, d1, …, dn)
功能:从标准正态分布中返回一个或多个样本值
np.random.normal(loc=0.0, scale=1.0, size=None) (常用)
loc:float 此概率分布的均值(对应着整个分布的中心centre)
scale:float 此概率分布的标准差(对应于分布的宽度,scale越大越矮胖,scale越小,越瘦高)
size:int or tuple of ints
输出的shape,默认为None,只输出一个值
np.random.standard_normal(size=None)
返回指定形状的标准正态分布的数组。
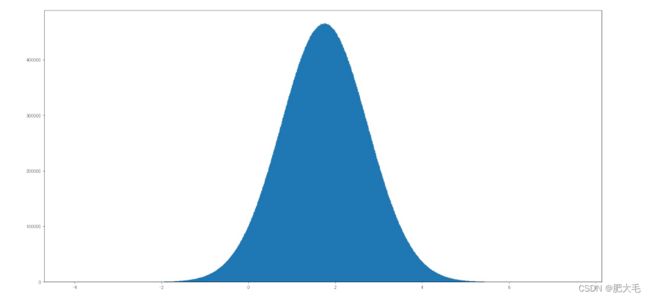
eg:生成均值为1.75,标准差为1的正态分布数据,100000000个
import numpy as np
import matplotlib.pyplot as plt
x1=np.random.normal(1.75,1,100000000)
# 创建画布
plt.figure(figsize=(20,10),dpi=100)
# 绘制直方图
plt.hist(x1,1000)
# 显示
plt.show()
3.4.2 均匀分布
均匀分布是概率论和统计学中的一种重要概率分布,也称为均匀随机变量分布。在均匀分布中,所有可能的结果在某个范围内是等可能发生的,没有任何一个结果比其他结果更有可能发生。
np.random.rand(d0, d1, …, dn) 返回[0.0,1.0)内的一组均匀分布的数。
np.random.uniform(low=0.0, high=1.0, size=None) (常用)
功能:从一个均匀分布[low,high)中随机采样,注意定义域是左闭右开,即包含low,不包含high. 参数介绍: low:
采样下界,float类型,默认值为0; high: 采样上界,float类型,默认值为1;
size:
输出样本数目,为int或元组(tuple)类型,例如,size=(m,n,k), 则输出mnk个样本,缺省时输出1个值。
返回值:ndarray类型,其形状和参数size中描述一致。
np.random.randint(low, high=None, size=None, dtype=‘l’)
从一个均匀分布中随机采样,生成一个整数或N维整数数组,
取数范围:若high不为None时,取[low,high)之间随机整数,否则取值[0,low)之间随机整数。
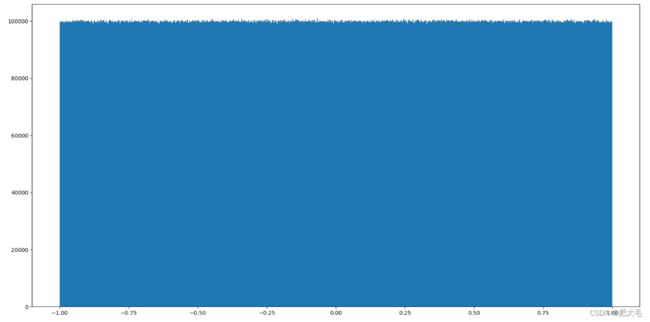
import numpy as np
import matplotlib.pyplot as plt
x1=np.random.uniform(-1,1,100000000)
# 创建画布
plt.figure(figsize=(20,10),dpi=100)
# 绘制直方图
plt.hist(x1,1000)
# 显示
plt.show()
3.5 形状修改
ndarray.reshape(shape, order)
返回一个具有相同数据域,但shape不一样的视图
行、列不进行互换
# 在转换形状的时候,一定要注意数组的元素匹配
stock_change.reshape([5, 4])
stock_change.reshape([-1,10]) # 数组的形状被修改为: (2, 10), -1: 表示通过待计算
ndarray.resize(new_shape)
修改数组本身的形状(需要保持元素个数前后相同)
行、列不进行互换
stock_change.resize([5, 4])
# 查看修改后结果
stock_change.shape
(5, 4)
ndarray.T
数组的转置
将数组的行、列进行互换
3.6 类型修改
ndarray.astype(type)
返回修改了类型之后的数组
3.7 数组的去重
np.unique()
import numpy as np
a=np.array([[1,2,3,4],[2,3,4,5],[5,6,7,7]])
b=np.unique(a)
b
3.8 数组的索引以及切片
直接进行索引,切片
对象[:, :] – 先行后列
import numpy as np
a=np.array([[1,2,3,4],[2,3,4,5],[5,6,7,7]])
a[0,0:2]
4.ndarray运算
4.1 逻辑运算
# 生成10名同学,5门功课的数据
>>> score = np.random.randint(40, 100, (10, 5))
# 取出最后4名同学的成绩,用于逻辑判断
>>> test_score = score[6:, 0:5]
# 逻辑判断, 如果成绩大于60就标记为True 否则为False
>>> test_score > 60
array([[ True, True, True, False, True],
[ True, True, True, False, True],
[ True, True, False, False, True],
[False, True, True, True, True]])
# BOOL赋值, 将满足条件的设置为指定的值-布尔索引
>>> test_score[test_score > 60] = 1
>>> test_score
array([[ 1, 1, 1, 52, 1],
[ 1, 1, 1, 59, 1],
[ 1, 1, 44, 44, 1],
[59, 1, 1, 1, 1]])
通用判断函数
np.all() 全部符合条件才为true
# 判断前两名同学的成绩[0:2, :]是否全及格
>>> np.all(score[0:2, :] > 60)
False
np.any() 有一个符合条件就为true
# 判断前两名同学的成绩[0:2, :]是否有大于90分的
>>> np.any(score[0:2, :] > 80)
True
np.where 三元运算符
# 判断前四名学生,前四门课程中,成绩中大于60的置为1,否则为0
temp = score[:4, :4]
np.where(temp > 60, 1, 0)
复合逻辑需要结合np.logical_and和np.logical_or使用
# 判断前四名学生,前四门课程中,成绩中大于60且小于90的换为1,否则为0
np.where(np.logical_and(temp > 60, temp < 90), 1, 0)
# 判断前四名学生,前四门课程中,成绩中大于90或小于60的换为1,否则为0
np.where(np.logical_or(temp > 90, temp < 60), 1, 0)
4.2 统计运算

进行统计的时候,axis 轴的取值并不一定,Numpy中不同的API轴的值都不一样,在这里,axis 0代表列, axis 1代表行去进行统计
# 接下来对于前四名学生,进行一些统计运算
# 指定列 去统计
temp = score[:4, 0:5]
print("前四名学生,各科成绩的最大分:{}".format(np.max(temp, axis=0)))
print("前四名学生,各科成绩的最小分:{}".format(np.min(temp, axis=0)))
print("前四名学生,各科成绩波动情况:{}".format(np.std(temp, axis=0)))
print("前四名学生,各科成绩的平均分:{}".format(np.mean(temp, axis=0)))
np.argmax(temp, axis=)
np.argmin(temp, axis=)
找出最大和最小元素的坐标