南京邮电大学数据结构实验一(线性表的基本运算及多项式的算术运算)
文章目录
-
- 一、顺序表
-
- (一)算法设计
-
- 1、数据结构
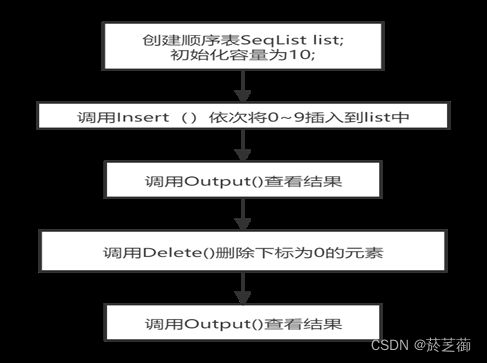
- 2、算法流程图绘制
- 3、模块设计
- (二)算法实现与分析
- (三)实验结果
- 二、带表头的单链表
-
- (一)算法设计
-
- 1、数据结构
- 2、算法流程图绘制
- 3、模块设计
- (二)算法实现与分析
- (三)实验结果
- 三、一元多项式的加法乘法
-
- (一)算法设计
-
- 1、数据结构
- 2、算法流程图绘制
- 3、模块设计
- (二)算法实现与分析
- (三)实验结果
- 四、全部代码
一、顺序表
(一)算法设计
1、数据结构
2、算法流程图绘制
3、模块设计
共分为5个模块,分别是初始化模块,查找模块,插入模块,输出模块和销毁模块。

(二)算法实现与分析
//顺序表的查找
Status Find(SeqList seqList, int i, ElemType* x) {
if (i < 0 || i > seqList.n - 1) {
return ERROR; //判断元素下标i是否越界
}
*x = seqList.element[i]; //取出element[i]的值通过参数x返回
return OK;
}
//初始化插入
Status Insert(SeqList* seqList, int i, ElemType x) {
int j;
if (i<-1 || i>seqList->n - 1) //判断下标i是否越界
return ERROR;
if (seqList->n == seqList->maxLength) //判断顺序表存储空间是否已满
return ERROR;
for (j = seqList->n - 1; j > i; j--) {
seqList->element[j + 1] = seqList->element[j]; //从后往前逐个后移元素
}
seqList->element[i + 1] = x; //将新元素放入下标为i+1的位置
seqList->n++; //长度+1
return OK;
}
查找算法:返回传入下标位置处的元素,时间复杂度为O(1);
插入算法:首先判断线性表空间是否已满,有剩余空间才可以继续插入,先将插入位置处以后的元素从最后开始依次后移,最后将待插入元素插入的第i+1的位置处,插入完成,时间复杂度为O(n);
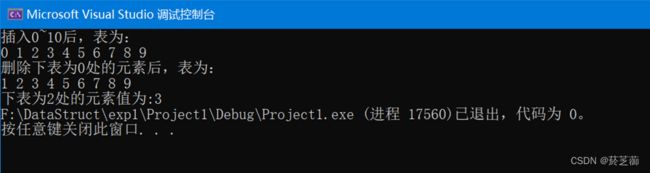
(三)实验结果
二、带表头的单链表
(一)算法设计
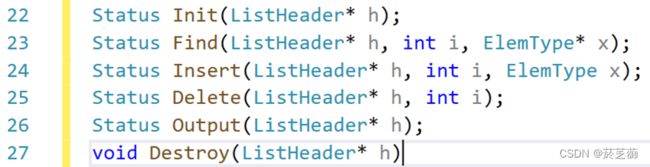
1、数据结构
typedef struct Node {
ElemType element; //结点的数据域
struct Node* link; //结点的指针域
}Node;
typedef struct {
struct Node* head; //表头结点
int n;
}ListHeader
2、算法流程图绘制
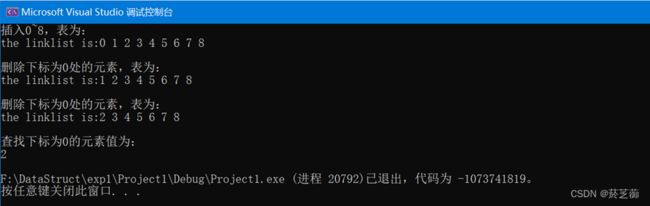
初始化:先为表头节点申请一个节点的空间,将0~8插入到链表中,显示当前链表的内容,删除下标为0处的元素,显示当前链表的内容,再次删除下标为0处的元素,显示当前链表的内容,查找下标为0的元素值为,显示内容。
3、模块设计
(二)算法实现与分析
//带表头结点单链表的插入
Status Insert(ListHeader* h, int i, ElemType x) {
Node* p, * q;
int j;
if (i<-1 || i>h->n - 1)
return ERROR;
p = h->head; //从头结点开始找ai元素所在的结点p
for (j = 0; j <= i; j++) {
p = p->link;
}
q = (Node*)malloc(sizeof(Node)); //生成新结点q
q->element = x;
// 将 q 插在 p 和 p->link 之间
q->link = p->link; //新结点q插在p之后
p->link = q;
h->n++;
return OK;
}
//带表头结点单链表的删除
Status Delete(ListHeader* h, int i) {
int j;
Node* p, * q;
if (!h->n) {
return ERROR;
if (i<0 || i>h->n - 1) {
return ERROR;
}
}
q = h->head;
for (j = 0; j < i; j++) {
q = q->link;
}
p = q->link;
// 将 q->link 改为 q->link->link; 即q的下一个节点的下一个,再将q的下一个节点删除
q->link = q->link->link;
free(p);
h->n--;
return OK;
}
插入算法分析:将指针移动到要插入的位置处,将待插入节点q插入到q的前一个节点p和p.link之间,插入即可完成。插入算法的时间复杂度为O(n);
删除算法分析:将指针移动到要删除的位置处,将待删除节点q的q->link 改为 q->link->link; 即q的下一个节点的下一个,再将q的下一个节点删除,删除即可完成,删除算法的时间复杂度为O(n);
(三)实验结果
三、一元多项式的加法乘法
(一)算法设计
1、数据结构
typedef struct PNode {
int coef; //系数
int exp; //指数
struct PNode* link;
}PNode;
typedef struct {
struct PNode* head;
}Polynominal;
多项式以链表的形式存储,每个链表的节点为多项式的一项,每一项包含三个成员变量,系数,指数和下一项的地址;
2、算法流程图绘制
首先创建两个多项式结构体指针,调用Creat函数对多项式进行初始化,即为多项式的头结点进行空间的申请,并且将头结点的阶数赋值为-1;从控制台获取所要输入的多项式的项数和各项的系数和阶数。调用Add和Multiply函数对多项式进行加法和乘法运算。
3、模块设计
(二)算法实现与分析
//多项式的相加,结果存入qx中
void Add(Polynominal* px, Polynominal* qx) {
PNode* q, * q1 = qx->head, * p, * p1, * temp; //q1指向qx的表头结点
p = px->head->link; //p指向多项式px的第一个结点
p1 = px->head;
q = q1->link; //q1是q的前驱
while (p->exp >= 0) {
while (p->exp < q->exp) { //跳过q->exp大的项
q1 = q;
q = q->link;
}
// 如果两多项式的阶数相等,则对应系数相加,结果存放在qx中
if (p->exp == q->exp) {
q->coef = q->coef + p->coef;
// 如果相加后系数为0
if (q->coef == 0) {
q1->link = q->link; //删除q
free(q); //释放q的空间
q = (PNode*)malloc(sizeof(PNode));
q = q1->link; //重置q指针
p = p->link;
}
else { //若相加后系数不为0
q1 = q; //q1后移
q = q->link;
p = p->link; //p也后移
}
}
else { //p->exp > q->exp的情况
temp = (PNode*)malloc(sizeof(PNode)); //以p的系数和指数生成新结点
temp->coef = p->coef;
temp->exp = p->exp;
temp->link = q1->link;
q1->link = temp;
q1 = q1->link;
p = p->link;
}
}
}
// 多项式乘法 (结果存放在qx1中)
void Multiply(Polynominal* px, Polynominal* qx) {
Polynominal qx1, qx2;
PNode* q1, * q2, * q3, * q4, * pre = (PNode*)malloc(sizeof(PNode)), * q;
qx1.head = (PNode*)malloc(sizeof(PNode)); //生成新多项式qx1
qx1.head->exp = -1;
qx1.head->link = qx1.head; //qx1改造成循环链表
q1 = px->head; //q1指向px的第一项
q2 = qx->head; //q2指向qx的第一项
while (q2->exp != -1) { //当q2的指数不为-1时,px先和qx的每一项相乘
q3 = (PNode*)malloc(sizeof(PNode)); //q3存放相乘的结果
// 系数相乘,阶数相加
q3->coef = q1->coef * q2->coef;
q3->exp = q1->exp + q2->exp;
if (qx1.head->link->exp == -1) { //q3插入到qx1多项式第一项中
q3->link = qx1.head->link;
qx1.head->link = q3;
pre = qx1.head->link;
}
else { //q3插入到qx1多项式最后一项中
q3->link = qx1.head;
pre->link = q3;
pre = pre->link;
}
q2 = q2->link;
}
// q1 指向 q1表达式的下一项
q1 = q1->link; //q1后移一位
while (q1->exp != -1) { //px剩下来每一项都和qx每一项相乘
q2 = q2->link;
qx2.head = (PNode*)malloc(sizeof(PNode)); //生成新多项式qx2
qx2.head->exp = -1;
qx2.head->link = qx2.head; // 指向自己
// 遍历 q2 的每一项
while (q2->exp != -1) {
q4 = (PNode*)malloc(sizeof(PNode));
q4->coef = q1->coef * q2->coef;
q4->exp = q1->exp + q2->exp;
if (qx2.head->link->exp == -1) {
q4->link = qx2.head->link;
qx2.head->link = q4;
pre = qx2.head->link;
}
else {
q4->link = qx2.head;
pre->link = q4;
pre = pre->link;
}
q2 = q2->link;
}
Add(&qx2, &qx1); //合并同类项
q1 = q1->link;
}
Output(qx1);
}
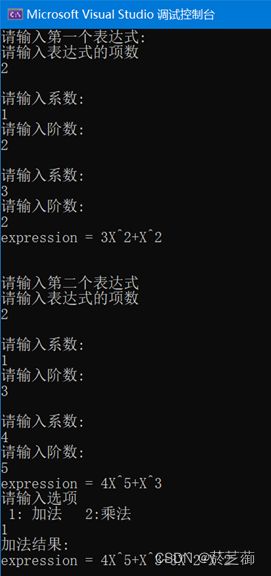
多项式的加法算法分析:函数传入两个多项式p和q,若p和q的某一项的阶数相等则对应系数相加生成新的项,若不相同则以原来的项的形式存入结果中。时间复杂度为O(n^2);
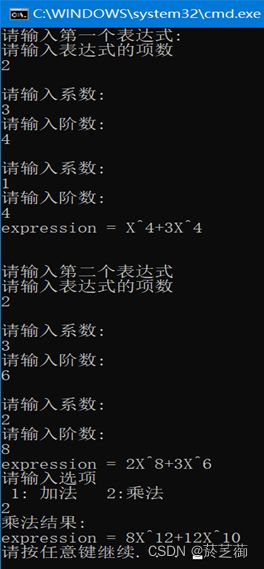
多项式的乘法算法分析:函数传入两个多项式p和q,先计算p的第一项和q的各项之积,计算结果存入新的多项式a1中,再计算p的第二项和q的各项之积,计算结果存入新的多项式a2中,调用Add(a1, a2)函数计算两次计算结果的和,循环以上步骤,即可求出两多项式的积。时间复杂度为O(n^2);
(三)实验结果
四、全部代码
全部代码