数据结构-快速排序
目录
概念
递归
hoare法
前后指针法
填坑法
非递归
栈 实现非递归
队列 实现非递归
快排优化
三数取中
小区间优化
快排性能
代码
概念
快速排序的基本思想是分治法,在待排序元素中任取一个元素作为基准,通过一定的操作使得一边的元素都小于该基准值,而另一边的元素都大于该基准值。通过这一趟排序划分被选为基准值的元素放在了最终正确的位置。然后对该基准值的左右两边元素分别递归地重复上述过程,直到左右两边的区间只有一个元素或者区间不存在,也就是待排序的所有元素都放在了其最终位置上。
递归
hoare法
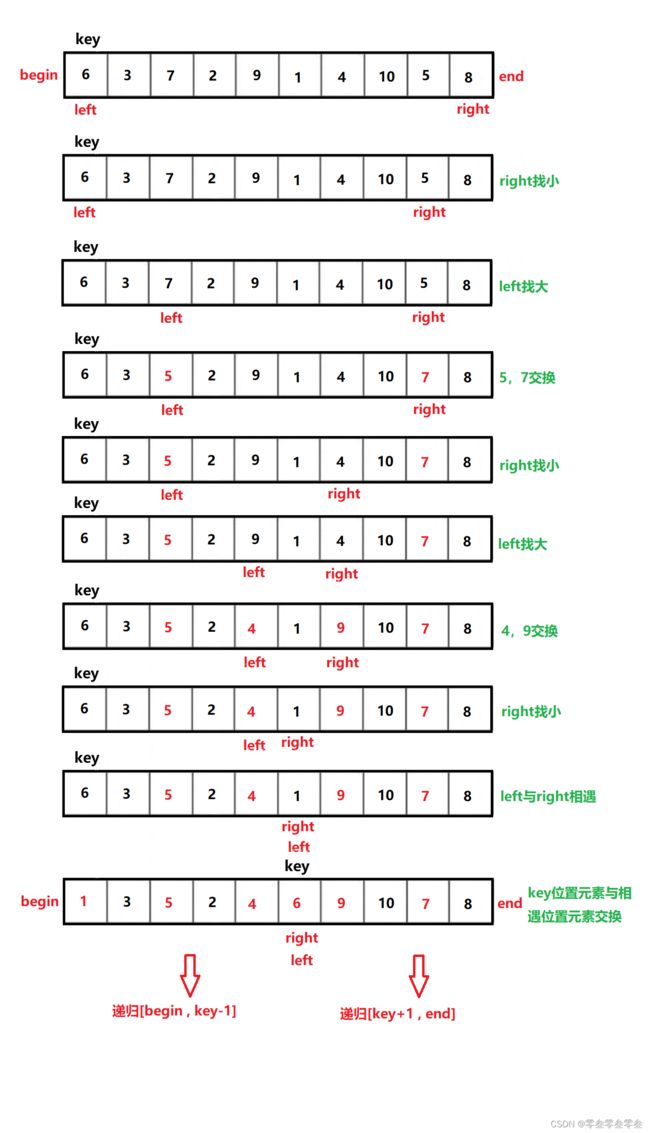
升序:
选最左边的元素作为基准值key,left和right最开始分别为区间第一个元素下标和区间最后一个元素下标。
右边right先走,找到比key小的元素就停下来,紧接着左边left再走,找到比key大的元素就停下来,然后将left,right对应位置的元素交换。
依次往复,如果left与right相遇则将key位置的元素与相遇位置的元素进行交换。然后再递归key元素的左右区间。
直到左右两边的区间只有一个元素或者区间不存在,也就是待排序的所有元素都放在了其最终位置上,快速排序完成。
void QuickSort(SortData* a, int n)
{
_QuickSort1(a,0,n-1);
}前后指针法
升序:
选[ begin , end ]区间的第一个元素作为基准值key,prev为区间第一个元素的位置,curr为区间第二个元素。
curr从第二个位置开始向后遍历该区间,如果遇到比基准值key小的元素,则先让prev位置加一,然后交换prev与curr位置的元素,curr继续遍历。
当curr遍历完该区间时,将key位置的元素与prev位置的元素进行交换。然后递归处理key左右区间的元素。
void QuickSort(SortData* a, int n)
{
_QuickSort2(a,0,n-1);
}填坑法
升序:
对于区间[begin , end],选区间第一个元素作为基准值key,保存key位置的元素,并记录key位置为最开始的坑位hole。
right从最后一个元素往前找比基准值key小的值,找到之后将该位置的元素填入坑位hole,填入之后更新坑位hole为right位置。
接着left从第一个元素往后找比基准值key大的值,找到之后将该位置的元素填入坑位hole,填入之后更新坑位hole为left位置。再接着right找小填坑,left找到大填坑。
如果left与right相遇则将保存好的基准值key填入相遇的坑位上。完成之后递归处理key的左右区间。
void QuickSort(SortData* a, int n)
{
_QuickSort3(a,0,n-1);
}非递归
栈 实现非递归
先将要排序的整个区间[ begin , end ]的范围入栈,然后判断栈是否为空进入循环,进入循环之后出栈取出区间范围进行一趟快排。
一趟快排结束之后,判断key位置的左右区间是否存在,如果存在则将左右区间的范围入栈,继续循环。
void QuickSortNonR(SortData* a, int n)
{
_QuickSortNonRStack(a, 0, n - 1);
}
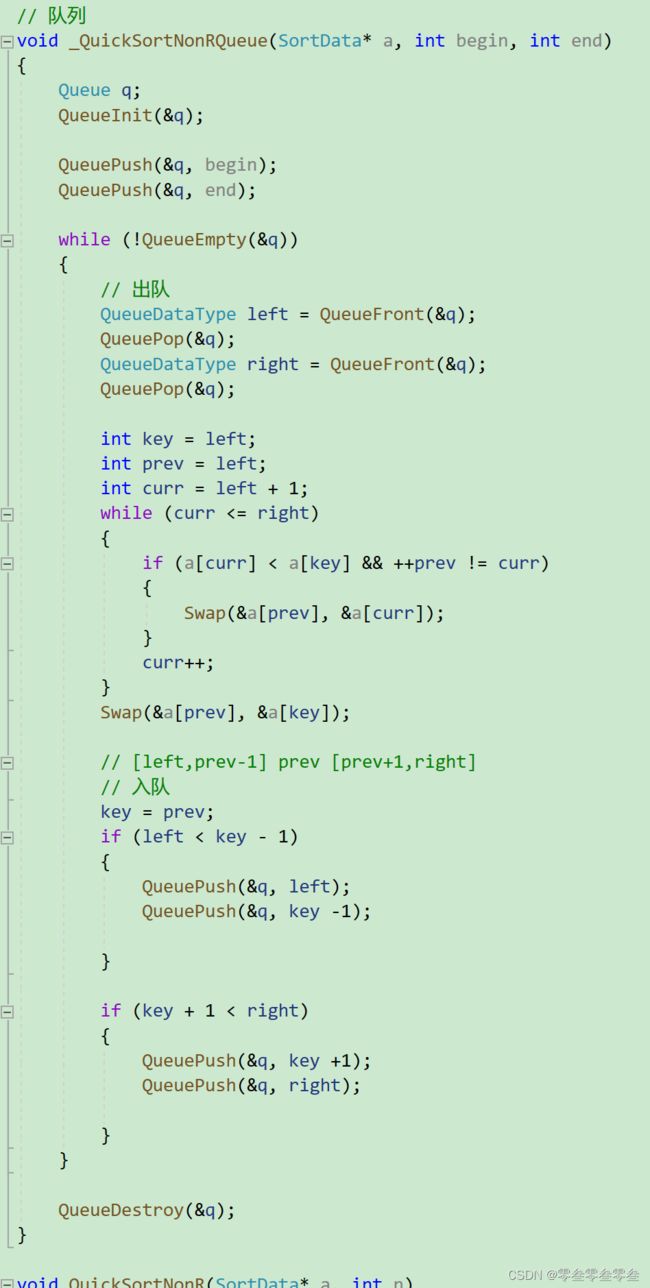
队列 实现非递归
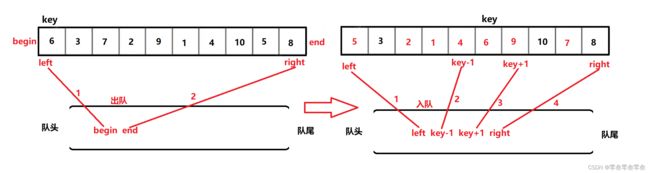
先将要排序的整个区间[ begin , end ]的范围入队列,然后判断队列是否为空进入循环,进入循环之后出队列取出区间范围进行一趟快排。
一趟快排结束之后,判断key位置的左右区间是否存在,如果存在则将左右区间的范围入队列,继续循环。
void QuickSortNonR(SortData* a, int n)
{
_QuickSortNonRQueue(a, 0, n - 1);
}
快排优化
三数取中
在区间的第一个位置,中间位置,最后位置的元素中选出中间大的元素,让中间大的元素被选为基准值key。
int GetMidIndex(SortData* a, int begin, int end)
{
int mid = (begin + end) / 2;
if (a[begin] > a[end])
{
if (a[mid] > a[begin])
{
return begin;
}
else if (a[end]>a[mid])
{
return end;
}
else
{
return mid;
}
}
else
{
if (a[mid] < a[begin])
{
return begin;
}
else if (a[end] < a[mid])
{
return end;
}
else
{
return mid;
}
}
} 小区间优化
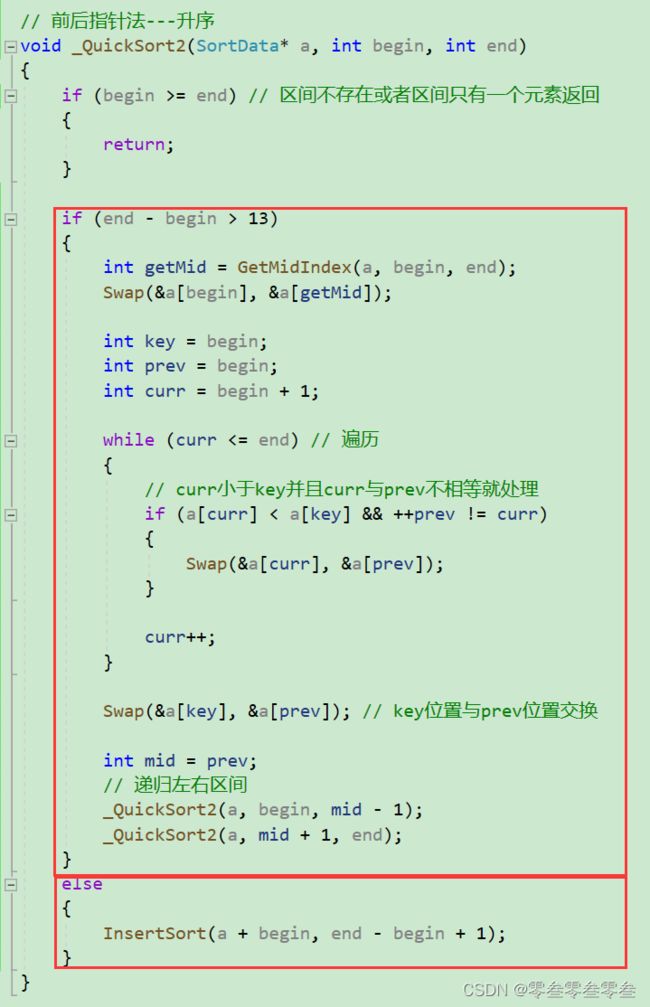
小区间优化
小区间优化主要是针对快速排序的递归版本,其思想是如果某一趟区间的长度小于某一长度则不需要继续进行递归快排,而是使用其他排序将该区间的元素排序好。(避免栈溢出?或者递归太深?降低空间复杂度?)
快排性能
- 空间复杂度:最好是O(log 2 N),最坏是O(N),平均是O(log 2 N)
- 时间复杂度:最好O(N*log 2 N),最坏O(N^2)
- 稳定性:不稳定
代码
// 快排的优化:1,三数取中 2,小区间优化
int GetMidIndex(SortData* a, int begin, int end)
{
int mid = (begin + end) / 2;
if (a[begin] > a[end])
{
if (a[mid] > a[begin])
{
return begin;
}
else if (a[end]>a[mid])
{
return end;
}
else
{
return mid;
}
}
else
{
if (a[mid] < a[begin])
{
return begin;
}
else if (a[end] < a[mid])
{
return end;
}
else
{
return mid;
}
}
}
// hoare法---升序
void _QuickSort1(SortData* a, int begin, int end)
{
if (begin >= end) // 区间不存在或者区间只有一个元素返回
{
return;
}
int getMid = GetMidIndex(a, begin, end);
Swap(&a[begin], &a[getMid]);
int key = begin; // 区间第一个元素作为基准值
int left = begin;
int right = end;
while (left < right)
{
while (left < right && a[right] >= a[key]) // 右边先找小
{
right--;
}
while (left < right && a[left] <= a[key]) // 左边再找大
{
left++;
}
Swap(&a[left], &a[right]); // 交换
}
Swap(&a[key], &a[left]); // key位置与相遇位置交换
int mid = left;
// 递归左右区间
_QuickSort1(a, begin, mid-1);
_QuickSort1(a, mid+1,end);
}
// 填坑法---升序
void _QuickSort3(SortData* a, int begin, int end)
{
if (begin >= end)
{
return;
}
int getMid = GetMidIndex(a, begin, end);
Swap(&a[begin], &a[getMid]);
int left = begin;
int right = end;
SortData key = a[left]; // 保存基准值,区间第一个元素为基准
int hole = left; // 初始坑位为基准值位置
while (left < right)
{
while (left < right && key <= a[right])
{
right--; // 先右边找小
}
a[hole] = a[right]; // 填坑
hole = right; // 更新坑位
while (left < right && key >= a[left])
{
left++; // 再左边找大
}
a[hole] = a[left]; // 填坑
hole = left; // 更新坑位
}
a[left] = key; // 保存的基准值填入相遇位置,也就是填入最新坑位
int mid = left;
// 递归左右区间
_QuickSort3(a, begin, mid - 1);
_QuickSort3(a, mid+1,end);
}
// 前后指针法---升序
void _QuickSort2(SortData* a, int begin, int end)
{
if (begin >= end) // 区间不存在或者区间只有一个元素返回
{
return;
}
if (end - begin > 13)
{
int getMid = GetMidIndex(a, begin, end);
Swap(&a[begin], &a[getMid]);
int key = begin;
int prev = begin;
int curr = begin + 1;
while (curr <= end) // 遍历
{
// curr小于key并且curr与prev不相等就处理
if (a[curr] < a[key] && ++prev != curr)
{
Swap(&a[curr], &a[prev]);
}
curr++;
}
Swap(&a[key], &a[prev]); // key位置与prev位置交换
int mid = prev;
// 递归左右区间
_QuickSort2(a, begin, mid - 1);
_QuickSort2(a, mid + 1, end);
}
else
{
InsertSort(a + begin, end - begin + 1);
}
}
void QuickSort(SortData* a, int n)
{
_QuickSort2(a,0,n-1);
}
// 栈
void _QuickSortNonRStack(SortData* a, int begin,int end)
{
Stack s;
StackInit(&s);
StackPush(&s, end);
StackPush(&s, begin);
while (!StackEmpty(&s))
{
// 出栈取出区间
StackDataType left = StackTop(&s);
StackPop(&s);
StackDataType right = StackTop(&s);
StackPop(&s);
int getMid = GetMidIndex(a, left, right);
Swap(&a[left], &a[getMid]);
int key = left;
int prev = left;
int curr = left + 1;
while (curr <= right)
{
if (a[curr] < a[key] && ++prev != curr)
{
Swap(&a[prev], &a[curr]);
}
curr++;
}
Swap(&a[prev], &a[key]);
// [left,prev-1] prev [prev+1,right]
// 入栈存放区间
key = prev;
if (key + 1 < right)
{
StackPush(&s, right);
StackPush(&s, key+1);
}
if (left < key - 1)
{
StackPush(&s, key-1);
StackPush(&s, left);
}
}
StackDestroy(&s);
}
// 队列
void _QuickSortNonRQueue(SortData* a, int begin, int end)
{
Queue q;
QueueInit(&q);
QueuePush(&q, begin);
QueuePush(&q, end);
while (!QueueEmpty(&q))
{
// 出队
QueueDataType left = QueueFront(&q);
QueuePop(&q);
QueueDataType right = QueueFront(&q);
QueuePop(&q);
int getMid = GetMidIndex(a, left, right);
Swap(&a[left], &a[getMid]);
int key = left;
int prev = left;
int curr = left + 1;
while (curr <= right)
{
if (a[curr] < a[key] && ++prev != curr)
{
Swap(&a[prev], &a[curr]);
}
curr++;
}
Swap(&a[prev], &a[key]);
// [left,prev-1] prev [prev+1,right]
// 入队
key = prev;
if (left < key - 1)
{
QueuePush(&q, left);
QueuePush(&q, key -1);
}
if (key + 1 < right)
{
QueuePush(&q, key +1);
QueuePush(&q, right);
}
}
QueueDestroy(&q);
}
void QuickSortNonR(SortData* a, int n)
{
//_QuickSortNonRStack(a, 0, n - 1);
_QuickSortNonRQueue(a, 0, n - 1);
}