稀疏矩阵:超级详细

稀疏矩阵

分了（三个文件）c语言版本

1、spametrix.h //稀疏矩阵函数的（声明）
2、SparseMetrix.cpp //稀疏矩阵函数的（定义）
3、main.cpp //验证内容

----------------------------------spametrix.h---------------------------------
#include
#define MaxSize 100 //稀疏矩阵所能容纳的：最大元素个数
#define N 4 //方阵（行列数）：常量
typedef int ElemType; //设置动态的：元素（存储内容）的数据类型

//稀疏矩阵的（元素）
typedef struct Node {
int row; //行下标
int column; //列下标
ElemType content; //元素：存储的内容
}smaNode;

//稀疏矩阵
typedef struct sparseMatrix {
int rowNum; //稀疏矩阵：行的：数目
int columnNum; //稀疏矩阵：列的: 数目
int num; //所容纳的：内容（非0）元素的个数
smaNode data[MaxSize]; //稀疏矩阵所能容纳的最大元素个数
}tsmatrix;

//1、产生稀疏矩阵A的三元组表示t。
void creatmat(tsmatrix& t, ElemType a[N][N]);

//2、输出三元组表示t。
void dispmat(tsmatrix t);

//3、求三元组表示t的转置矩阵tb。
void tranmat(tsmatrix t, tsmatrix& tb);

//4、三元组元素的赋值，x必须为非0元
bool assign(tsmatrix& t, ElemType x, int i, int j);

//5、指定位置的元素赋值给变量
bool value(tsmatrix t, ElemType& x, int i, int j);

//6、求c=a+b。
bool matadd(tsmatrix a, tsmatrix b, tsmatrix& c);

//7、返回三元组t中稀疏矩阵A的A[i][j]的值。
int getvalue(tsmatrix t, int i, int j);

//8、求c=a×b。
bool matmul(tsmatrix a, tsmatrix b, tsmatrix& c);
----------------------------------SparseMetrix.cpp------------------------
#include “spametrix.h”

//1、产生稀疏矩阵A的三元组表示t。
void creatmat(tsmatrix& t, ElemType a[N][N])
{
t.rowNum = N; //行：数目赋值
t.columnNum = N; //列：数目赋值
t.num = 0; //元素的个数：初始为0

for (int i = 0; i < N; i++)
{
	for (int j = 0; j < N; j++) 
	{
		//当元素内容（不为0时）存入稀疏矩阵
		if (a[i][j] != 0) {	
			t.data[t.num].row = i;				//元素的：行号
			t.data[t.num].column = j;			//元素的：列号
			t.data[t.num].content = a[i][j];	//元素的：内容
			t.num++;							//稀疏矩阵内元素个数：加1
		}
	}
}

}

//2、输出三元组表示t。
void dispmat(tsmatrix t)
{
printf("\t行\t列\t元素个数\n");
printf("\t%d\t%d\t%d\n", t.rowNum, t.columnNum, t.num);
printf("----------------------------------------------------\n");

for (int i = 0; i < t.num; i++) 
{
	printf("\t%d\t%d\t%d\n", t.data[i].row, t.data[i].column, t.data[i].content);
}

printf("\n");			//换行

}

//3、求三元组表示t的转置矩阵tb。
void tranmat(tsmatrix t, tsmatrix& tb)
{
tb.rowNum = t.columnNum; //确定tb的行：数目
tb.columnNum = t.rowNum; //确定tb的列：数目
tb.num = t.num; //确定tb的元素个数

int k = 0;
//当t的元素个数不为：0时
if (0 != t.num) {
	for (int i = 0; i < t.columnNum; i++) {			//固定列：因为转置后就是行
		for (int j = 0; j < t.num; j++) {			//在每一列中：进行一次所有：元素的匹配列
			if (t.data[j].column == i) {			//当元素列，与固定列匹配时：该元素存入，行变列，列变行
				tb.data[k].column = t.data[j].row;
				tb.data[k].row = t.data[j].column;
				tb.data[k].content = t.data[j].content;
				k++;
			}
		}
	}
}

}

//4、三元组元素的赋值，x必须为非0元
bool assign(tsmatrix& t, ElemType x, int i, int j)
{
//检验参数的合法性
if (0 == x) {
return false;
}

for (int p = 0; p < t.num; p++) {
	if (t.data[p].row == i && t.data[p].column == j) {
		t.data[p].content = x;
		return true;
	}
}

return false;

}

//5、指定位置的元素赋值给变量
bool value(tsmatrix t, ElemType& x, int i, int j)
{
for (int p = 0; p < t.num; p++) {
//查找到指定坐标的：元素
if ((t.data[p].row == i) && (t.data[p].column == j)) {
x = t.data[p].content;
return true;
}
}

//三元组内（没有该元素）
x = 0;
return false;

}

//6、求c=a+b。
bool matadd(tsmatrix a, tsmatrix b, tsmatrix& c)
{
//检验参数的合法性：看a,b是的初始矩阵是否为：同型矩阵
if (a.rowNum != b.rowNum || a.columnNum != b.columnNum) {
return false;
}

//声明：中间变量
int i = 0;						//i作为记录：a的元素的个数
int j = 0;						//j作为记录：b的元素的个数
int k = 0;						//j作为记录：c的元素的个数
ElemType v;						//中间变量

//给c的行、列、元素个数进行赋值
c.rowNum = a.rowNum;				//行数目 == a的：行数目
c.columnNum = b.columnNum;			//列数目 == a的：列数目

//相加有三种情况:
while (i < a.num && j < b.num) {			//此时锁定：元素递增范围要（小于）三元组的（元素个数）
	//1、当a的元素行 > b的元素行
	if (a.data[i].row > b.data[j].row) {
		//将b的第j个元素存入c中
		c.data[k].row = b.data[j].row;				//存入：行坐标
		c.data[k].column = b.data[j].column;		//存入：列左边了
		c.data[k].content = b.data[j].content;		//存入：元素内容

		k++;										//c元素个数加1
		j++;										//b元素个数加1
	}//2、当a的元素行 < b的元素行
	else if (a.data[i].row < b.data[j].row) {
		//将a的第i个元素存入c中
		c.data[k].row = a.data[i].row;				//存入：行坐标
		c.data[k].column = a.data[i].column;		//存入：列左边了
		c.data[k].content = a.data[i].content;		//存入：元素内容

		k++;										//c元素个数加1
		i++;										//a元素个数加1
	}//3、当a的元素行 == b的元素行
	else {
		//此时：又有三种情况
		if (a.data[i].column > b.data[j].column) {//(1)、a的列 > b的列
			//将b的第j个元素存入c中
			c.data[k].row = b.data[j].row;				//存入：行坐标
			c.data[k].column = b.data[j].column;		//存入：列左边了
			c.data[k].content = b.data[j].content;		//存入：元素内容

			k++;										//c元素个数加1
			j++;
		}
		else if(a.data[i].column < b.data[j].column){	//(2)、a的列 < b的列
			//将a的第i个元素存入c中
			c.data[k].row = a.data[i].row;				//存入：行坐标
			c.data[k].column = a.data[i].column;		//存入：列左边了
			c.data[k].content = a.data[i].content;		//存入：元素内容

			k++;										//c元素个数加1
			i++;										//a元素个数加1
		}//(3)、a的列 == b的列
		else {
			//将a和b的第i个元素：内容相加存入c中
			v = a.data[i].content + b.data[j].content;						//存入：元素内容
			if (0 != v) {
				c.data[k].row = a.data[i].row;								//存入：行坐标
				c.data[k].column = a.data[i].column;						//存入：列左边了
				c.data[k].content = v;
				k++;														//c元素个数加1
			}
			i++;															//a元素个数加1
			j++;															//b元素个数加1
		}		
	}
}

c.num = k;
return true;
}

//7、返回三元组t中稀疏矩阵A的A[i][j]的值。
int getvalue(tsmatrix t, int i, int j)
{
for (int p = 0; p < t.num; p++) {
//查找到指定坐标的：元素
if ((t.data[p].row == i) && (t.data[p].column == j)) {
return t.data[p].content;
}
}

//三元组内（没有该元素）
return 0;

}

//8、求c=a×b。
bool matmul(tsmatrix a, tsmatrix b, tsmatrix& c)
{

//检验参数的合法性：看a的列，是否等于b的行
if (a.columnNum != b.rowNum) {
	return false;
}

//给c进行行、列数目赋值：
c.rowNum = a.rowNum;			//a的（行数）是：c的（行数）
c.columnNum = b.columnNum;		//b的（列数）是：c的（列数）
c.num = 0;						//c的元素个数初始为：0
ElemType temp;					//作为中间变量

for (int i = 0; i < a.rowNum; i++) {				//固定a的行
	for (int j = 0; j < b.columnNum; j++) {			//固定b的列
		temp = 0;									//作为中间变量
		for (int k = 0; k < a.columnNum; k++) {		//移动b固定列的：行标
			//此时a的行不变：列变化； b的列不变，行变化
			temp += getvalue(a, i, k) * getvalue(b, k, j);		
		}
		if (0 != temp) {
			c.data[c.num].row = i;					//元素行下标
			c.data[c.num].column = j;				//元素列下标
			c.data[c.num].content = temp;			//元素内容
			c.num++;								//元素个数加1
		}
	}

}
return true;
}

----------------------------------main.cpp-------------------------------------
#include “spametrix.h”

int main(void)
{
//1、生产2个4 * 4的矩阵(a1, b1)：用于测试
ElemType a1[N][N] = { {1, 0, 3, 0}, {0, 1, 0, 0},{0, 0, 1, 0},{0, 0, 1, 1} };
ElemType b1[N][N] = { {3, 0, 0, 0}, {0, 4, 0, 0},{0, 0, 1, 0},{0, 0, 0, 2} };

//2、创建三个：存储:稀疏矩阵的变量（a, b, c, d）用于测试
tsmatrix a, b, c;

//3、产生稀疏矩阵的三元组:存入a, b内
creatmat(a, a1);
creatmat(b, b1);

//4、分别：输出三元组(a, b)
puts("a三元组如下：\n");
dispmat(a);

puts("b三元组如下：\n");
dispmat(b);

//5、给三元组赋值
if (assign(a, 5, 1, 1)) {
	printf("赋值成功！！\n");
}
else {
	printf("赋值失败！！\n");
}
printf("赋值后的内容为：\n");
dispmat(a);


//6、求三元组(a, b)分别转置后的三元组
tranmat(a, c);			//a进行转置：保存到c
puts("（a转置后）的三元组如下：\n");
dispmat(c);

tranmat(b, c);			//b进行转置：保存到c
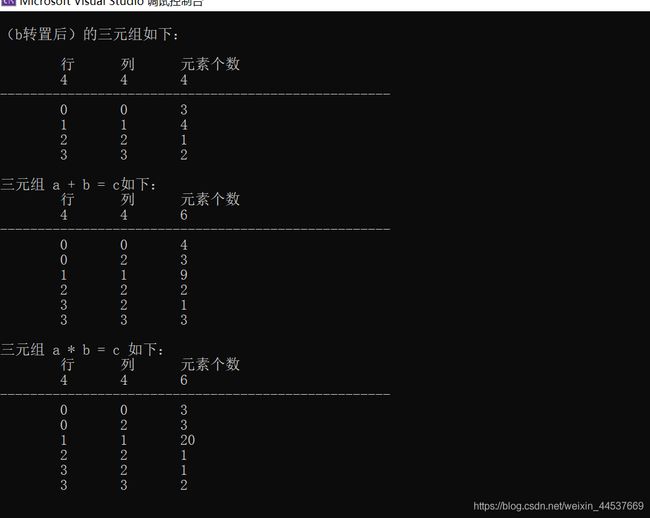
puts("（b转置后）的三元组如下：\n");
dispmat(c);


//7、做三元组的加法
printf("三元组 a + b = c如下：\n");
matadd(a, b, c);
dispmat(c);

//8、做三元组的乘法
printf("三元组 a * b = c 如下：\n");
matmul(a, b, c);
dispmat(c);


return 0;
}