Python数据分析2——Numpy基本操作

目录

Numpy基本操作

创建N-维数组对象

数组的数据类型

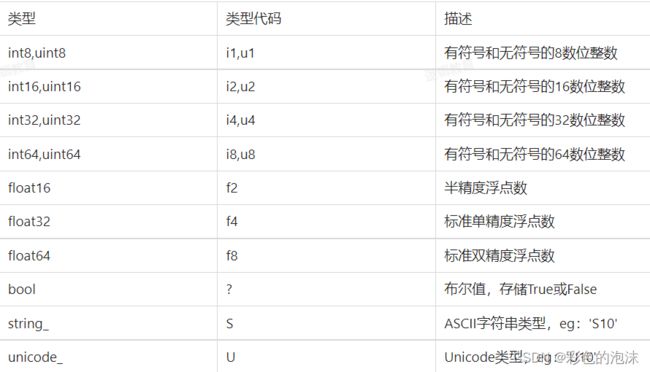
Numpy数据类型 

​编辑

查看数组数据类型

指定数组的数据类型

数组形状

arr.ndim

arr.shape

N-维数组对象

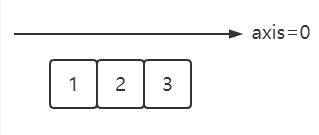
一维

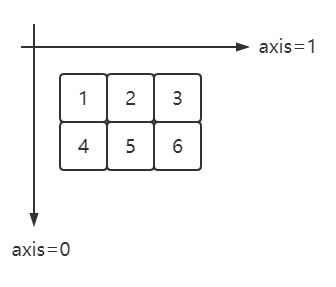
二维

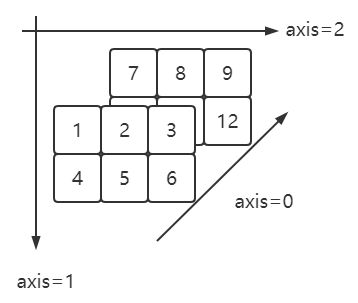
三维

重塑数组

一维转多维

多维转一维

数组转置与换轴

创建数组的其他函数

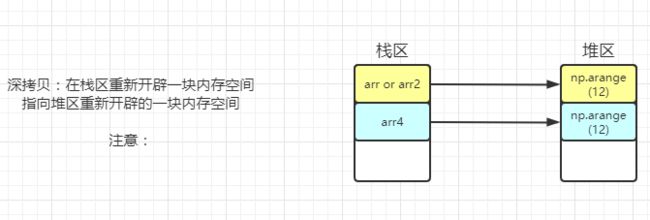
数组的拷贝

理解

不拷贝

浅拷贝

深拷贝

Numpy数组算术

数组与标量的算术操作

两个等尺寸数组的算术操作

广播机制

数组拼接

切片

将条件逻辑作为数组操作

Numpy操作本地数据

写入本地数据

读取本地数据

NaN与inf

nan与inf介绍

NaN特点

如何处理nan

random模块

np.random.seed

np.random.rand

np.random.randn

np.random.normal

np.random.randint

np.random.choice

np.random.shuffle

np.random.permutation

数据分割

np.hsplit

np.vsplit

np.array_split

常用函数

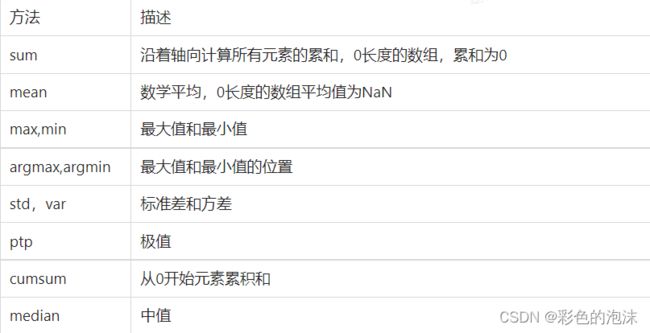
聚合函数 

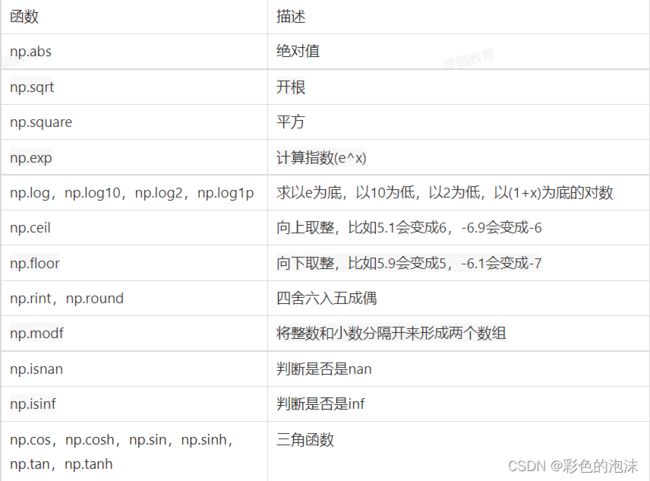
一元函数

二元函数

自定义函数的使用

数组的线性代数运算

Numpy的扩展

Numpy应用——图像处理

SciPy库的使用

引用物理数学常数

图像处理

线性代数的运算

---

Numpy基本操作

创建N-维数组对象

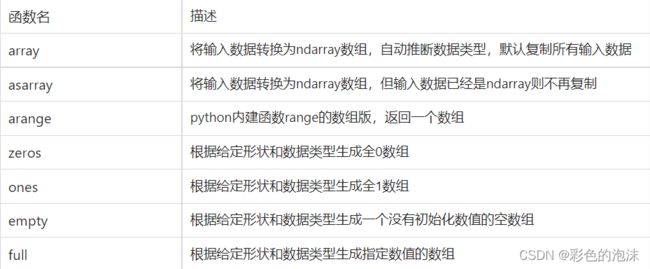
生成数组最简单的方式就是使用array函数。array函数接收任意的序列型对象，生成一个新的包含传递数据的Numpy数组。

• numpy.array(object)

import numpy as np
li = [1,2,3,4]
arr = np.array(li)
arr 

• numpy.arange([start,] stop[, step,])

import numpy as np
arr = np.arange(1,5)
arr

注意

• ndarray数组是一个通用的多维同类数据容器，意味着数组里面每一个元素均为相同类型。

数组的数据类型

Numpy数据类型 

查看数组数据类型

• arr.dtype                  # 查看数组的数据类型

import numpy as np
arr = np.arange(1,5)
arr.dtype  

注意

• np.array()会自动推断生成数组的数据类型

指定数组的数据类型

• numpy.array(object,dtype=None)    创建数组时通过dtype直接指定

import numpy as np
arr = np.array([1,2,3],dtype='f8')
arr
arr.dtype

• arr.astype(dtype)    # 修改数组数据类型

import numpy as np
arr = np.array([1,2,3])
arr = arr.astype(np.float32)
arr.dtype

数组形状

arr.ndim

查看数组的维度，返回值为整数

arr.shape

查看数组的，返回值为元组

N-维数组对象

一维

二维

import numpy as np
arr = np.array([[1,2,3],[4,5,6]])
arr

三维

import numpy as np
arr = np.array([[[1,2,3],[4,5,6]],[[7,8,9],[10,11,12]]])
arr
arr.shape

重塑数组

一维转多维

• arr.reshape(shape,order="C")

• • shape为数组重塑形状
  • order表示重塑方向

• • • C顺序(行方向)重塑
    • F顺序(列方向)重塑

import numpy as np
arr = np.arange(6)
arr = arr.reshape(2,3)
arr

多维转一维

• arr.flatten()
• arr.ravel()

数组转置与换轴

• arr.transpose()       # 转置
• arr.T                       # 转置
• arr.swapaxes()        # 换轴

创建数组的其他函数

数组的拷贝

理解

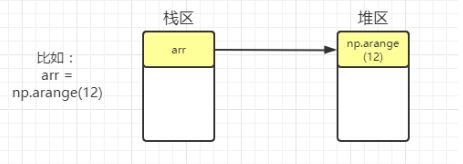
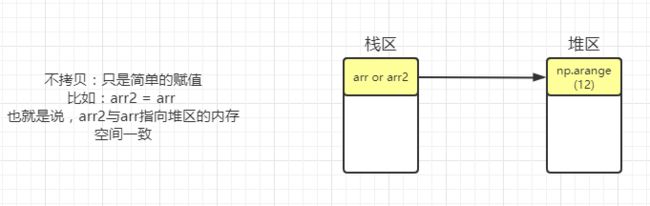
不拷贝

import numpy as np

arr = np.arange(12)
arr2 = arr
arr is arr2     
arr2[1] = 20   
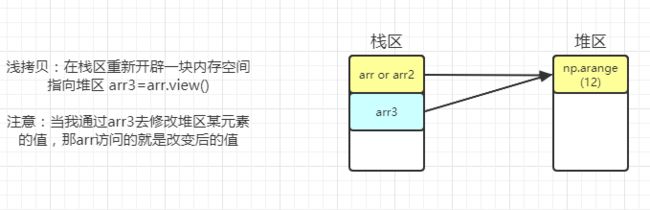
arr

浅拷贝

arr3 = arr.view()
arr3
arr3 is arr      

arr3[0] = 10
arr

深拷贝

arr4 = arr.copy()
arr4 is arr       

arr4[2] = 20     
arr

Numpy数组算术

数组之所以重要是因为它允许我们进行批量操作数据并且没有任何for循环。也被称为向量化。

数组与标量的算术操作

数组与标量的算术操作会把计算参数传递给数组的每一个元素。

import numpy as np
arr = np.arange(6).reshape(2,3)
arr+1

两个等尺寸数组的算术操作

两个等尺寸数组的算术操作实际上是逐元素操作。

arr = np.arange(1,7).reshape(2,3)
arr
arr+arr   
arr/arr  
arr-arr   

广播机制

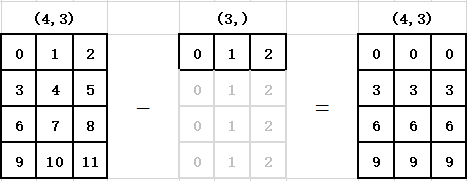
广播机制规则：如果两个数组的后缘维度（trailing dimension，即从末尾开始算起的维度）的轴长度相符或其中一方的长度为1，则认为他们是广播兼容的。广播会在缺失和（或）长度为1的维度上进行。

与列数相同并且只有1行的数组之间进行运算

• 在其丢失的轴上进行，也就是0轴广播

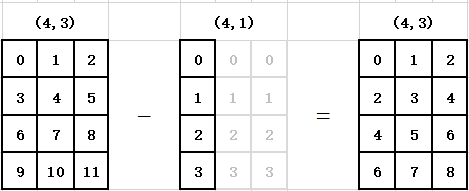
与行数相同并且只有1列的数组之间进行运算

• 在其长度为1轴上进行，此处也就是1轴广播

注意

• 维度完全不一致，则无法广播。

数组拼接

• np.vstack()     垂直拼接
• np.hstack()    水平拼接

注意

• 水平拼接需要对应行数一致,垂直拼接需要对应列数一致。

切片

一维索引与切片

同python中的内建数据类型list一致。

注意

• 索引默认从0开始
• 切片左闭右开
• 步长为整数

二维索引与切片

• 二维数组递归方式获取
• 二维数组逗号分隔获取(行,列)

• • 取单行        arr[x1,:]
  • 取连续行    arr[x1:x2,:]
  • 取分开行    arr[[x1,x2],:]
  • 取子矩阵    arr[x1:x2,y1:y2]
  • 取点           arr[[x1,x2],[y1,y2]]

注意

• 当有需要修改数组当中的值时，我们可以直接取值进行赋值。
• 当数组与标量进行比较时，数组当中每个元素与标量进行比较，返回bool值。与此同时,该比较也可以作为索引，被称为布尔索引。比如arr[arr>20]

将条件逻辑作为数组操作

numpy.where()函数是三元表达式 x if condition else y 的向量化版本。

• np.where(condition, [x, y])    # 当满足条件，执行x，否则执行y

arr = np.arange(16).reshape(4,4) 
arr1 = np.where(arr<10,0,10)
arr1

Numpy操作本地数据

写入本地数据

• np.savetxt(fname)

• • fname                      文件路径
  • dtype                       数据类型
  • delimiter                  分隔符
  • fmt='%.18e'             写入文件的格式，例如：%d，%.2f，%.18e
  • converters               对数据预处理。比如{0:func}第0列进行func函数预处理
  • header                    指定为表头

scores = np.random.randint(0,100,size=(40,2))  # 期中与期末考试

np.savetxt("scores.csv",scores,delimiter=",",fmt="%d",header="期中,期末",comments="") 

读取本地数据

• np.loadtxt(fname)       

• • fname                      文件路径
  • dtype                       数据类型
  • delimiter                  分隔符
  • skiprows                  跳过行
  • comment                 如果行的开头为 # 就会跳过该行
  • usecols                    是指使用(0,2)两列
  • unpack                    每一列当成一个向量输出,而不是合并在一起
  • converters               对数据预处理。比如{0:func}第0列进行func函数预处理

np.loadtxt("scores.csv",delimiter=",",skiprows=1)

NaN与inf

nan与inf介绍

nan：not a number 表示不是一个数字，属于浮点类。

inf：np.inf 表示正无穷，-np.inf表示负无穷，属于浮点类。

NaN特点

• nan与inf都是float类型

c = np.nan
c
type(c)    # float

d = np.inf
d
type(d)    # float

• 两个nan是不相等的

• • 该特性可以用来判断nan的个数

• • • np.count_nonzero() 计算非零的个数
    • np.isnan() 判断数组元素是否是NaN，返回为bool值

np.nan == np.nan   # False

• np.nan与任何数值计算都是nan

np.arange([2,np.nan,3])+100  # arry([102,nan,103])

也正因为，np.nan与任何值计算都是nan所以在运算时，会带来较大的误差。一般我们都会将其处理掉。

如何处理nan

直接删除缺失值所在行，但是当数据量较小时，这样处理会有影响整体的数据。更优雅的做法，是当求和时，将np.nan处理为0；当求均值时，将np.nan处理为非nan的均值。

random模块

np.random为我们提供了许多获取随机数的函数。其实是python内置random模块进行的封装。

参考网址：Legacy Random Generation — NumPy v1.22 Manualhttps://numpy.org/doc/stable/reference/random/legacy.html#numpy.random.RandomState

np.random.seed

用于指定随机数生成时所用算法开始的整数值，如果使用相同的seed()值，则每次生成的随即数都相同，如果不设置这个值，则系统根据时间来自己选择这个值，此时每次生成的随机数因时间差异而不同。一般没有特殊要求不用设置。以下代码：

np.random.seed(1)
print(np.random.rand()) 

np.random.rand

生成一个值为[0,1)之间的数组，形状由参数指定，如果没有参数，那么将返回一个随机值。示例代码如下：

data = np.random.rand() #生成一个0-1之间的随机数

np.random.randn

生成均值(μ)为0，标准差（σ）为1的标准正态分布的值。示例代码如下：

data = np.random.randn(2,3) #生成一个2行3列的数组，数组中的值都满足标准正太分布

np.random.normal

可以自己选择正太分布的均值和方差，如：

# 生成一个均值为4，方差为4的正太分布的4*4的矩阵
arr = np.random.normal(4,4,size=(4,4))
print(arr)

np.random.randint

生成指定范围内的随机数，并且可以通过size参数指定维度。示例代码如下

data = np.random.randint(10,size=(3,5)) #生成值在0-10之间，3行5列的数组

np.random.choice

从一个列表或者数组中，随机进行采样。或者是从指定的区间中进行采样，采样个数可以通过参数指定

data = np.arange(100)
res = np.random.choice(data,size=(2,3)) #从data中随机采样，生成2行3列的数组

np.random.shuffle

把原来数组的元素的位置打乱。会改变原数组；

a = np.arange(10)
np.random.shuffle(a) #将a的元素的位置都会进行随机更换

np.random.permutation

与 np.random.shuffle 的使用方法和作用一致，但不会改变原数组；

np.random.permutation(arr)

数据分割

np.hsplit

该函数在视觉上呈现 左右 方向上的分割，及axis=1上的分割；如：

a1 = np.arange(16.0).reshape(4, 4)
a1

np.hsplit(a1,2)   # 分割2部分  左右
# 注意只能等切割，如上面的4*4矩阵，可以设置参数为1，2，4

np.vsplit

该函数在视觉上呈现 上下 方向上的分割，及axis=0上的分割；如：

np.vsplit(a1,2)    # 分割2部分  上下

np.array_split

可以自己选择在哪一维度上进行分割，可以对多维度进行操作，如：

np.array_split(a1,2,axis=0) 

np.array_split(a1,2,axis=1)

常用函数

聚合函数 

a1 = np.arange(12).reshape(3,4)

np.sum(a1)         # 全部相加
np.sum(a1,axis=0)  # 计算0轴的累和
np.sum(a1,axis=1)  # 计算1轴方向的累和

一元函数

# 有正数 也有 负数
arr = np.random.uniform(-10,10,size=(3,5))  
arr

# 求绝对值
np.abs(arr)

np.rint(4.4)   # 四舍
np.rint(4.5)   # 五舍    

np.rint(4.6)   # 六入
np.rint(5.5)   # 五成双

二元函数

np.add(arr,arr)  # 加法运算

arr[np.logical_and(arr>0,arr<5)]  # 取出arr中 >0 并且 <5 的数

自定义函数的使用

np.apply_along_axis

如：

a = np.array([[9,8,7,1],[8,7,6,5],[6,4,1,3]])
a

 需求：将上面的数组在axis=0上,对数组去除最大值和最小值，求均值。

实现1.使用lambda：

# 将函数应用到数组上
np.apply_along_axis(lambda x:x[(x!=x.max())&(x!=x.min())].mean(),axis=1,arr=a)

实现2.先定义好def：

def f(x):
    res = x[(x!=x.max())&(x!=x.min())].mean()
    return res

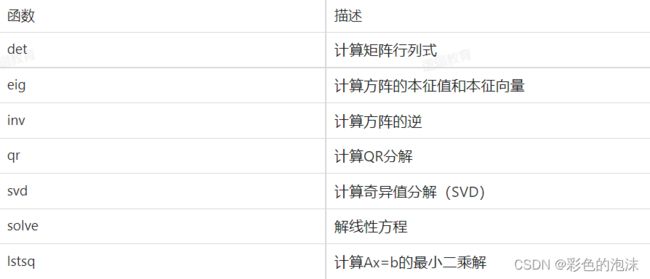
np.apply_along_axis(f,axis=1,arr=a)

数组的线性代数运算

线性代数（例如矩阵乘法、矩阵分解、行列式以及其他数学函数）是任何数据分析库的重要组成部分。Numpy也提供这样的能力，那么如何进行线性代数的乘法呢？

我们直接使用 np.dot(arr,arr.T) 进行运算即可。

除此之外， numpy.linalg 中封装了一组标准的矩阵分解运算以及诸如逆运算、行列式等功能。

Numpy的扩展

Numpy应用——图像处理

使用PIL库来完成，代码展示如下：

from PIL import Image    # pip install pillow

Image.open('demo.jpg')

使用numpy转换为数组对象：

im = np.array(Image.open('demo.jpg'))
im

可以做如下操作，如改变方向，和改变颜色，等：

# 图像方向
b = im[::-1]


# 颜色
c = [255,255,255] - im
c

最后导出：

Image.fromarray(c.astype('uint8'))

SciPy库的使用

主要应用于：

• 数学
• 科学
• m工程计算

依赖于Numpy

引用物理数学常数

# 物理和数学常数
from scipy.constants import pi,g,c,h,G,R,Avogadro

pi

图像处理

# 图像处理
from scipy import ndimage
import matplotlib.image as mpimg
import matplotlib.pyplot as plt

如：做高斯模糊处理

face = mpimg.imread('demo.jpg')

face1 = ndimage.gaussian_filter(face,9)

plt.imshow(face1)

线性代数的运算

scipy.linalg 中封装了一组标准的矩阵分解运算以及诸如逆运算、行列式等功能。具体函数使用与numpy基本一致。