人工智能之数学（概率方面）

我们经常使用的统计机器学习算法，或者是神经网络模型中，数学作为最基础的根基，融合了高等数学中的微分学、概率、线性代数、凸优化等方面，每一个方面深入后都是有很多的益处，但是本着先实用，在进行学习的原则。所以主要是理解相关数学符号，理解统计学习中一些和概率相关的算法推导，即可。

基础

概率： 一件事情发生的概率，等于该事件发生的数目除以所发生的数目。例如电影院观影人数为100人，女生50人，男士50人，你看到一个人是女生的可能就是50除以100，概率为0.5。当然这是不考虑任何判别因素的情况下。这个数字也会根据你的判断问题的改变而改变。如果此时你看到的是在男生休息室附近的人，此时有98个男的，2个女的。这个时候看到女士的概率则降成了0.02。

似然函数： P(x|y)是根据已知结果去推测固有性质的可能性，通过一定的历史数据观测的来。例如女生50人中有25个长头发，25个短头发。那么她是女人并且是长头发的概率就是
P(long hair | woman)=0.5。50个男人中2个长头发，那么P(long hair | man)=0.04。从上面我们可以知道，条件概率可以直接得到，不过P(long hair | woman)和P( woman| long hair)不同。

条件概率： P(y|x)，已知条件发生，出现目标的概率是多少。

联合概率： P(XY)，代表X和Y都发生的可能性，就是联合概率。例如我们在电影院取票，排在我身后的人是短发女生的概率，我们不回头，没有任何参考。首先女生的概率是P(woman)=50/100=0.5,女生中又是短发的概率P(short hair | woman) = 25/50 = 0.5。则P(woman with short hair) = P(woman) * P(short hair | woman)=0.25。换个方式，先考虑
短发的概率 P(short hair) = （25+48）/100 = 0.73，短发中是女生的概率 P(woman | short hair ) = 25 /（25+48）。P(woman with short hair) = P(woman) * P(short hair | woman)=P(short hair) * P(woman | short hair )

边际概率： P(X)，例如长发的概率是多少，也就是男生长发和女生长发的概率和。P(woman with long hair)和P(man with long hair)的和。

贝叶斯定理

我们根据上面的基础知识和实例来理解一下贝叶斯定理。我们在电影院排队取票，看到前面的人头发是长发。其他的特征不做考虑。那么前面的人是女生的概率是多少。根据条件概率知识P(woman | long hair )不同 P(long hair | woman)， P(long hair | woman)=0.5。所以我们借助于联合概率。*P(woman with long hair) = P(woman) * P(long hair | woman)=P(long hair) * P(woman | long hair )。根据这个式子就可以求出P(woman | long hair )。

先验概率： 指代事情发生之前，通过观察，人为总结，或者背景知识中知道的概率。P(woman)。统计概率

后验概率： P(long hair | woman)指代我们根据一定的原因，推出结果的可能性。

全概率公式： 边际概率在实际问题中不好运算。所以选择全概率公式。事件组B1，B2，…满足俩俩互斥，即 Bi ∩ Bj = ∅ ，i≠j ， i,j=1，2，…，且P(Bi)>0,i=1,2,…；B1∪B2∪…=Ω ，则称事件组 B1,B2,…是样本空间Ω的一个划分，设 B1,B2,…是样本空间Ω的一个划分，A为任一事件，则：

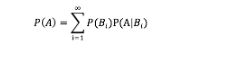
直观说，全概率公式的存在目的是求解贝叶斯公式中P(X),因为P(X)求解较为困难。思路是将A分解成小事件，通过小事件的概率相加，对A进行分解时，不是直接进行分割。想找到样本空间划分B1,B2,…Bn,这样事件A就被事件AB1,AB2,…ABn分解成了n部分，即A=AB1+AB2+…+ABn, 每一Bi发生都可能导致A发生相应的概率是P(A|Bi)。P(A)=P(AB1)+P(AB2)+…+P(ABn)=P(A|B1)P(B1)+P(A|B2)P(B2)+…+P(A|Bn)P(Bn)