强化学习案例_强化学习系列案例 | 蒙特卡洛方法实现21点游戏策略

查看本案例完整的数据、代码和报告请登录数据酷客(cookdata.cn)案例板块。

快速获取案例方式：数据酷客公众号内发送“强化学习”。

蒙特卡洛方法(Monte Carlo method)是20世纪40年代中期提出的一种以概率统计为指导的重要数值计算方法。其名字来源于摩洛哥的赌城蒙特卡洛，象征着概率。蒙特卡洛方法在金融工程学，宏观经济学，计算物理学等领域应用广泛。

本案例将介绍基于蒙特卡洛的强化学习的基本思想，并求解智能体玩21点游戏的策略。

1.蒙特卡洛方法的基本思想

一般蒙特卡洛方法可以分成两类：

一种类型是所求解的问题本身具有内在的随机性，借助计算机的运算能力可以直接模拟这种带有随机性的过程。例如在核物理研究中，分析中子在反应堆中的传输过程。中子与原子核作用受到量子力学规律的制约，人们只能知道它们相互作用发生的概率，却无法准确获得中子与原子核作用时的位置以及裂变产生的新中子的行进速率和方向。科学家依据其概率进行随机抽样得到裂变位置、速度和方向，这样模拟大量中子的行为后，经过统计就能获得中子传输的范围，作为反应堆设计的依据。

另一种类型是所求解的问题可以转化为某种随机分布的特征数，比如随机事件出现的概率，或者随机变量的期望值。通过随机抽样的方法，以随机事件出现的频率估计其概率，或者以抽样的数字特征估算随机变量的数字特征，并将其作为问题的解，这种方法多用于求解复杂的多维积分问题。

首先我们实现一个经典的例子，用蒙特卡洛方法求的值。

假设在一个单位正方形内放置半径为1的1/4个圆:

1. 在正方形内生成一些随机点，可以观察到一些点位于圆内，而另一些点位于圆外
2. 根据方程计算位于圆内的点的个数
3. 通过将圆内点个数与正方形内点个数之比乘以4来计算的值

如果增大随机点个数(样本个数)，可以更好的近似的值。

import matplotlib.pyplot as plt
import random
%matplotlib inline

# 输入随机点的数量
nbPoints=int(input("请输入随机点的数量："))

# 初始化圆内点数
dansCercle=0
# 初始化圆内圆外点的储存
x_axis_1,x_axis_2,y_axis_1,y_axis_2=[],[],[],[]

for i in range(nbPoints):
# 生成随机点
    x = random.random()
    y = random.random()

# 判断随机点是否在圆内，计算欧氏距离
if (x**2+y**2)**0.5<1:
        dansCercle+=1
        x_axis_1.append(x)
        y_axis_1.append(y)
else:
        x_axis_2.append(x)
        y_axis_2.append(y)

# 计算π的模拟近似值
print("π的模拟近似值是:", dansCercle/nbPoints*4)

# 绘图
fig = plt.figure(1, figsize=(8, 6))
plt.scatter(x_axis_1,y_axis_1,s=20,c="blue")
plt.scatter(x_axis_2,y_axis_2,s=20,c="red")
plt.title("蒙特卡洛方法模拟")
plt.show()

请输入随机点的数量：10000
π的模拟近似值是: 3.1368

2. 状态-动作价值函数

2.1 状态-动作价值函数的引入

值迭代法(value iteration)和策略迭代法(policy iteration)是在环境模型已知的情况下求解最佳策略，这类方法可以统称为model-based方法，即环境模型已知或为环境建模。但在很多情况下，环境的模型是未知的，我们不清楚状态之间如何转移，甚至不清楚全部的状态空间长什么样子，这种情况下，无法利用Bellman方程求解价值函数，也无法由价值函数得到最佳策略：

我们引入状态-动作价值函数，令：

则

通过直接求解，便可以得到最佳策略。下面我们给出的具体定义：

策略下状态-动作价值函数

处于状态，且立即采取动作，并且后续按照策略操作能获得的累积期望奖励，即：

状态-动作价值函数

处于状态，且立即采取动作，并且后续按照最佳策略操作能获得的累积期望奖励，即：

2.2 Q表(Q-table)

虽然对环境信息了解不充分，但我们可以通过与环境交互，产生一系列的观测数据来学习。在状态空间、动作空间离散的情况下，可以建立一个表格，称为Q表，来存储状态-动作对应的，横向表示状态，纵向表示动作，通过不断迭代，更新Q表的值，最终使用Q表进行决策，根据找出最佳策略：

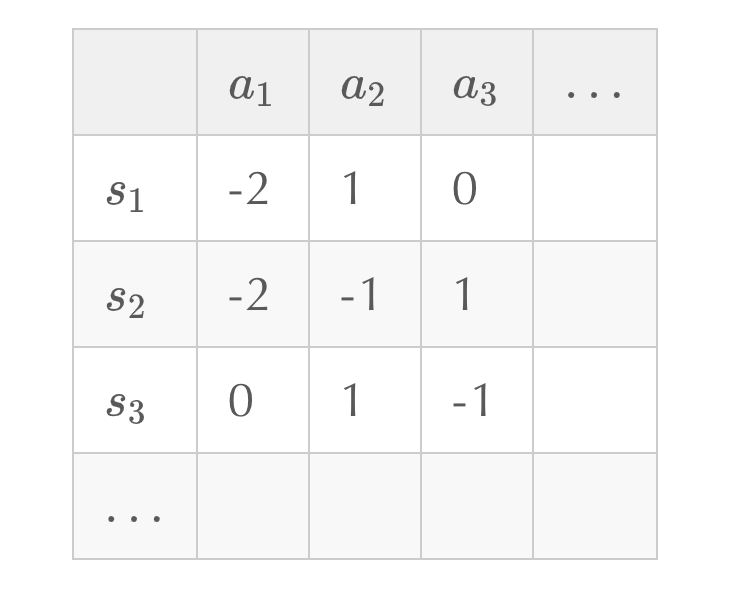
不对环境建模，直接与环境交互产生数据进行学习的强化学习方法称为model-free方法，基于蒙特卡洛的强化学习方法就是其中典型的一种。

3 基于蒙特卡洛的强化学习方法

基于蒙特卡洛的强化学习方法不需要已知的环境模型，而是通过不断地与环境交互，获得多个观测序列，再利用多次观测序列得到的经验平均来估计期望从而求解价值函数。

记一次观测为：
记时刻状态的累积奖励为：

以策略下状态-动作价值函数为例，在策略下，计算次交互产生的状态-动作对的累积奖励的平均，以此来近似累积奖励的期望：

3.1 首次访问(first visit)和每次访问(every visit)

在近似值函数的过程中，同一个状态可能在一个完整的观测序列中重复出现，从而衍生出两种计算方法：

首次访问：

利用每次试验观测序列中第一次访问到状态-动作对后的累积奖励。

每次访问：

利用每次试验观测序列中所有访问到状态-动作对后的累积奖励。

其中表示第次试验第次访问状态-动作对后的累积奖励，表示状态-动作对的访问次数。

3.2 -soft策略

为保证算法更具有探索性，我们采用如下的-soft策略来代替-greedy策略：

其中表示探索率，表示处于状态可以执行的动作个数。-soft是随机性策略，可以通过采样得到需要执行的动作。

3.3 蒙特卡洛控制(Monte Carlo control)

所谓蒙特卡洛控制就是利用蒙特卡洛方法求解最佳策略的过程，蒙特卡洛控制有许多方法，在这里我们介绍-soft策略的在线(on-policy)首次访问蒙特卡洛控制算法：

on-policy指的是采样策略和评估提升策略是同一策略，比如上述算法流程中采样策略和评估提升策略都是-soft策略。与之相对的是off-policy，即采样策略和评估提升策略不是同一策略，这个我们会在今后的案例中进一步介绍。

4.1 21点游戏的规则

21点是一个十分具有趣味性的牌类游戏，最早出现在16世纪，起源于法国，法语称为ving-et-un(20和1)。后传入英国并广泛流传，如果玩家拿到黑心“A”和黑心“J”会给予额外的奖励，英文名称叫黑杰克(Blackjack)。

该游戏由2到6人进行，一名庄家，其余为玩家，使用除大小王之外的52张扑克牌，玩家的目标是使手中牌的点数之和不超过21点且尽量大。游戏过程中会给庄家和玩家每人发两张牌，一张为明牌，一张为暗牌。玩家可以根据手中牌点数和的大小与庄家手中牌点数来要牌 (hit) 并决定何时停牌(stick) 。当选择继续要牌后，若三张牌数的总和大于21点，则算自爆，游戏失败；停止请求牌后，庄家翻开扣着的牌，并抽牌，直到所有点数之和是17点或大于17点后，和玩家进行比较，谁的点数更靠近21，谁获胜；如果庄家自爆，玩家获胜；若两方点数相同，则为平局；具体点数计算规则如下：

• 1.2到10的点数就是其牌面的数字
• 2.J,Q,K三种牌均记为10点
• 3.玩家A(Ace牌)可以当作1点，也可以当作11点，11点时称为“可用”；庄家A只能当作1点

4.2 形式化为MDP问题

我们首先载入Gym中的21点游戏环境'Blackjack-v0'：

import gym
env = gym.make('Blackjack-v0')

状态空间

一个三元组，包括玩家当前牌面的总点数、庄家明牌的点数、玩家是否使用了Ace牌：

env.observation_space

Tuple(Discrete(32), Discrete(11), Discrete(2))

玩家当前牌面的总点数的范围为0~31，为方便基于Q表的算法轻松建立索引，所以包含了无法到达的状态，如0、31等
庄家明牌的点数的范围为0~10，0是无法到达的状态，其余表示A~10
玩家使用Ace牌表示为True，反之为False。

动作空间

0表示停止要牌(stick)，1表示继续要牌(hit)：

env.action_space

Discrete(2)

奖励

每局游戏中，玩家胜利奖励为1，失败奖励为-1，平局奖励记为0。

策略

-soft策略，玩家在某状态下，选择要牌(stick)还是停牌(hit)的概率。

4.3 实现蒙特卡洛控制

首先导入一些相关的库：

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import pandas as pd

用空字典创建一个Q表，用于存储：

q_table = {}

设置探索率为0.2，并创建空字典作为策略表，存储在状态s下选择动作a的概率：

explore_rate = 0.2

soft_policy = {}

创建空字典用于保存对的累积奖励:

returns = {}

接下来我们创建一个函数，用于产生一个完整的观测序列。在产生观测序列的同时，向Q表q_table、策略表soft_policy以及累积奖励表returns中添加产生的状态-动作对，并初始化的Q值为0，要牌和停牌的概率各为0.5。

import numpy as np

def generate_episode(q_table, soft_policy):

# 初始化一个列表，用于保存观测序列
    episode = []

# 初始化环境
    s = env.reset()

whileTrue:
# 若状态s第一次出现，将它添加到q_table和soft_policy中
if s notin q_table.keys():
            q_table[s] = {0:0.0, 1:0.0} # 初始化0(stick)和1(hit)的Q值
            soft_policy[s] = [0.5, 0.5] # 初始化0(stick)和1(hit)的概率，各为0.5
            returns[s] = {0:[], 1:[]} # 初始化空列表用于存储累积奖励

# 利用soft_policy采样一个动作
        a = np.random.choice([0, 1], p=soft_policy[s], size=1)[0]

# 与环境交互，产生奖励与下一状态
        next_s, reward, done, _ = env.step(a)

# 将状态s、动作a、奖励reward添加到eposide中
        episode.append((s, a, reward))

# 到达终止状态，循环结束
if done:
break

# 更新当前状态为下一状态
        s = next_s

return episode

下面我们进行蒙特卡洛控制，通过不断与环境交互产生观测序列，从而更新Q表和策略。设置迭代次数为50000次，在每一次迭代中，首先利用当前策略产生一个观测序列，接着初始化累积奖励，之后反向遍历观测序列中的每一步，从后往前计算累积奖励，然后判断每一步的状态-动作对是否首次出现在观测序列中，若是则将累积奖励加入对应的累积奖励列表returns中，计算列表中元素的均值进而更新Q表中Q值，最后更新策略。

# 设置迭代次数
n_iter = 50000

for i in range(n_iter):

# 产生一个观测序列
    episode = generate_episode(q_table, soft_policy)

# 初始化累积奖励
    G = 0.0
# 反向遍历观测序列中的每一步
for t in range(len(episode))[::-1]:
# 分别保存每一步的状态、动作和奖励
        state, action, reward = episode[t]
# 计算累积奖励
        G = G + reward
# 判断(state, action)是否第一次出现
if (state, action) notin [j[:2] for j in episode[:t]]:

# 将G加入(state, action)的Returns中
            returns[state][action].append(G)
# 更新Q表中的Q值
            q_table[state][action] = np.mean(returns[state][action])

# 更新策略
            a_star = np.argmax(list(q_table[state].values()))
            soft_policy[state][a_star] = 1 - explore_rate + explore_rate/2
            soft_policy[state][1 - a_star] = explore_rate/2

迭代结束后，我们将Q表q_table转换为DataFrame进行观察：

q_dataframe = pd.DataFrame([list(item.values()) for item in list(q_table.values())],
                           index = list(q_table.keys()),
                           columns = ['stick', 'hit'])
q_dataframe.iloc[:10, :]

	stick	hit
(14, 10, False)	-0.536998	-0.545932
(14, 3, False)	-0.307692	-0.405063
(9, 6, False)	-0.043478	0.066667
(12, 6, False)	-0.225000	-0.471698
(20, 1, False)	0.183236	-0.800000
(8, 3, False)	-0.625000	-0.215909
(18, 3, False)	0.098485	-0.727273
(12, 4, False)	-0.267974	-0.260870
(6, 7, False)	-0.629630	0.057143
(17, 7, True)	-0.048780	0.142857

利用Q表可以得到最终的游戏策略：

policy = pd.Series(np.where(q_dataframe.values[:, 0]>q_dataframe.values[:, 1], 'stick', 'hit'),index=list(q_table.keys()))
policy[:10]

(14, 10, False)    stick
(14, 3, False)     stick
(9, 6, False)        hit
(12, 6, False)     stick
(20, 1, False)     stick
(8, 3, False)        hit
(18, 3, False)     stick
(12, 4, False)       hit
(6, 7, False)        hit
(17, 7, True)        hit
dtype: object

5.总结

在本案例中，我们首先利用蒙特卡洛方法模拟了求解值的过程，从而了解的蒙特卡洛方法的基本思想；接着引入了状态-动作价值函数，说明了在环境模型信息不充分时，可以通过与环境交互产生数据学习价值函数，从而求解最佳策略；然后介绍了基于蒙特卡洛的强化学习方法的基本思想，包括首次访问和每次访问、-soft策略和蒙特卡洛控制等；最后利用蒙特卡洛方法通过求解Q表得到了21点游戏的策略。其实基于蒙特卡洛的强化学习方法还有许多改进，例如增量更新计算、重要性采样等，大家可以进行进一步尝试。