C语言进阶第一课 -----------深度剖析数据在内存中的存储
作者前言
✨✨✨✨✨✨
作者介绍:
作者id:老秦包你会,
简单介绍:
喜欢学习C语言和python等编程语言,是一位爱分享的博主,有兴趣的小可爱可以来互讨
个人主页::小小页面
gitee页面:秦大大
一个爱分享的小博主 欢迎小可爱们前来借鉴_______________________________________________________
______________________________________________________________________
目录
- 数据类型详细介绍
- 整形在内存中的存储:原码、反码、补码
- 大小端字节序介绍及判断
- 浮点型在内存中的存储解析
——————————————————————————————————————
数据类型介绍
前面我已经介绍了C语言中 常用的数据类型
char // 字符数据类型short // 短整型int // 整形long // 长整型long long // 更长的整形float // 单精度浮点数double // 双精度浮点数
类型的基本归类
charunsigned charsigned charshortunsigned short [ int ]signed short [ int ]intunsigned intsigned intlongunsigned long [ int ]signed long [ int ]
int a;signed int a;unsigned int a;
floatdouble
构造类型(自定义):
> 数组类型> 结构体类型 struct> 枚举类型 enum> 联合类型 union
指针类型
int * pi ;char * pc ;float* pf ;void* pv ;
如:int main(void)
整形在内存中的存储
int a = 20;
int b = 10;
会各自在内存开辟四个字节的空间进行存储
其实计算机能够处理的数据是二进制的,整形和浮点型数据在内存也都是以二进制的形式进行存储。
整数的二进制表示形式有3种:原码、反码、补码
正数的原码、反码、补码相同,
负数的反码是符号位不变,其他位取反, 补码是在反码的基础上加1
#include
int main()
{
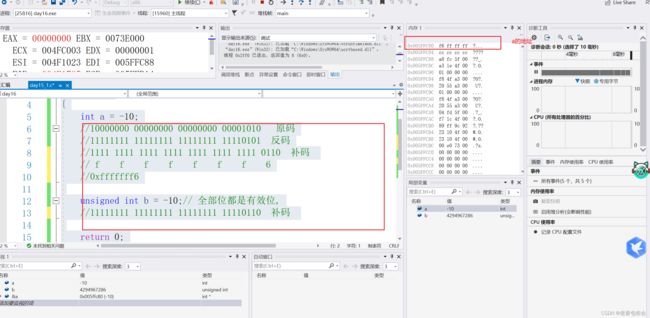
int a = -10;
//10000000 00000000 00000000 00001010 原码
//11111111 11111111 11111111 11110101 反码
//1111 1111 1111 1111 1111 1111 1111 0110 补码
// f f f f f f f 6
//0xfffffff6
unsigned int b = -10;// 全部位都是有效位,
//11111111 11111111 11111111 11110110 补码
return 0;
}
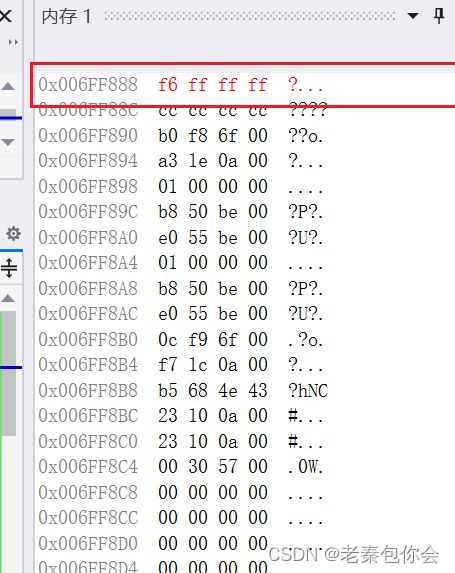
4个二进制位表示一个十六进制位
四个比特位 表示一个十六进制位, 两个十六进制位表示一个字节
#include
int check_sys()
{
int i = 1;
return (*(char *)&i);
}
int main()
{
int ret = check_sys();
if(ret == 1)
{
printf("小端\n");
}
else
{
printf("大端\n");
}
return 0;
} #include
int my_end(int a)
{
int i = 0;
int sum = 0;
for (i = 0; i < 8; i++)
{
//计算a补码最右端的8位二进制之和
int b = (a >> i) & 1;
sum = sum + b * pow(2, i);
}
return sum;
}
int main()
{
int a = 0;
scanf("%d", &a);
char* p = (char*)&a;
//返回*p开始地址指向的那个字节的大小
int num = my_end(a);
if (*p = num)
{
printf("小端存储");
}
else
{
printf("大端存储");
}
return 0;
} 练习2
#include
int main()
{
char a = -1;
//10000000 00000000 00000000 00000001 原码
//11111111 11111111 11111111 11111110 反码
//11111111 11111111 11111111 11111111
//因为a为字符变量,只能存储一个字节,存储后8位
//a-- 11111111
signed char b = -1;
//b -- 11111111
unsigned char c = -1;
//c -- 11111111
printf("%d %d %d", a, b, c);
//%d是十进制的形式,打印有符号位的整数
//因为abc三个未够4个字节,发生整形提升
//a和b 11111111 11111111 11111111 11111111
//c 00000000 00000000 00000000 11111111
return 0;
} 注意一下:%d是十进制的形式打印有符号位的整数
#include
int main()
{
unsigned char a = -128;
//10000000 00000000 00000000 10000000
//11111111 11111111 11111111 01111111
//11111111 11111111 11111111 10000000
//a > 10000000
// 整形提升
// 11111111 11111111 11111111 10000000 有符号的
// 00000000 00000000 00000000 10000000 无符号的
printf("%d\n", a);
printf("%u", a);
return 0;
}  赋值后,先整形提升,把整形提升后的值存储进去,对于无符号数,原码、反码、补码是相同的,
赋值后,先整形提升,把整形提升后的值存储进去,对于无符号数,原码、反码、补码是相同的,
char 的范围为-128~127
unsigned char 为0~255
#include
int main()
{
int i = -20;
//10000000 00000000 00000000 00010100
//11111111 11111111 11111111 11101011
//11111111 11111111 11111111 11101100
unsigned int j = 10;
//00000000 00000000 00000000 00001010
printf("%d", j + i);
//11111111 11111111 11111111 11110110
//因为%d为有符号十进制输出
// 在%d看来都是有符号的 转换为原码》10000000 00000000 00000000 00001010
return 0;
} #include
#include
int main()
{
unsigned int i = 0;
for (i = 9; i >= 0; i--)
{
//无符号的整数都大于等于0的
printf("%u\n", i);
Sleep(1000);
}
return 0;
} #include
#include
int main()
{
char arr[1000];
int i;
for (i = 0; i < 1000; i++)
{
arr[i] = -1 - i;
}
printf("%d", strlen(arr));
return 0;
} 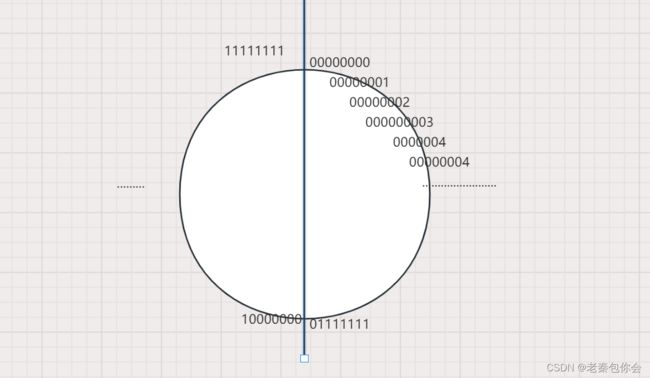 这道题主要体现出char的范围为-128~127 ,不会超过127
这道题主要体现出char的范围为-128~127 ,不会超过127
浮点型在内存中的存储
一这张图为例,可以看出整数的存储形式和浮点数的存储形式是不一样的
浮点数存储规则
二进制:101.1
利用科学计数法,因为是2进制向左移动两位写成 1.011 * 2^2 ,又因为是正数,所以再乘上(-1)^0
最终写成 (-1)^0 * 1.011* 2^2 即S=0 M=1.011 E=2
所以计算机只要存储S M E就行了
include
int main()
{
float a = 5.5;
//101.0
//(-1)^0 * 1.011 * 2^2
// S = 0, M = 1.011, E= 2
// 因为E要加上127后存入即 E= 129
//0100 0000 1011 0000 0000 0000 0000 0000
//4 0 b 0 0 0 0 0
return 0;
}
指数E从内存中取出还可以再分成三种情况
0 01111110 00000000000000000000000
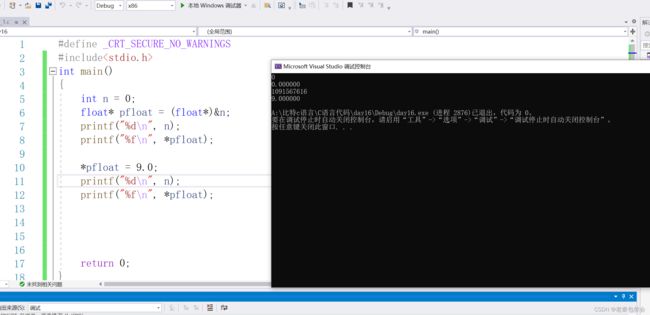
int main()
{
int n = 9;
//0000 0000 0000 0000 0000 0000 0000 1001
float* pfloat = (float*)&n;
printf("%d\n", n);
//0 00000000 00000000000000000001001
// S = 0 E = 1-127 = -126 M = 0.00000000000000000001001
//(-1)^S * M * 2^E
printf("%f\n", *pfloat);
*pfloat = 9.0;
// 1001.0
//(-1)^0 * 1.0010 * 2^3
// E = 3+127
//0 10000010 00100000000000000000000
printf("%d\n", n);
printf("%f\n", *pfloat);
return 0;
}