算法刷题笔记
特定方法
KMP算法:字符串匹配
逆波兰表达式:计算值
斐波那契数:动态规划
强制类型转换:整型->字符串:to_string,字符串->整型:stoi
一、数组
- 数组:下标从0开始,内存地址空间连续(所以数组元素只能覆盖,不能删除),C++中二维数组地址也连续
- vector:底层是数组,但本身是容器,内存也是连续的,与数组不同的是,vector可以动态扩展
1.二分查找(704)
二分查找的前提:数组有序且无重复元素
二分查找关键点是循环不变原则,即while循环中每次边界处理坚持根据区间定义
class Solution {
public:
int search(vector& nums, int target) {
int left = 0;
int right = nums.size() - 1;
while (left <= right) {
int middle = left + (right - left) / 2; // 若先计算left + right可能会超出int边界
if (nums[middle] > target) right = middle - 1;
if (nums[middle] < target) left = middle + 1;
if (nums[middle] == target) return middle;
}
return -1;
}
};
2.移除元素(27)
双指针法:通过一个快慢指针在一个for循环下完成两个for循环的工作(指针从同一侧出发,移动方向相同)
// 时间复杂度O(n),空间复杂度O(1)
class Solution {
public:
int removeElement(vector& nums, int val) {
int slowIndex = 0;
for (int fastIndex = 0; fastIndex < nums.size(); fastIndex++) {
if (nums[fastIndex] != val) nums[slowIndex++] = nums[fastIndex];
}
return slowIndex;
}
};
3.有序数组的平方(977)
- 如果先求平方再用sort排序则时间复杂度为O(n+logn)
- 采用双指针法(指针从两端出发,移动方向相反)
// 时间复杂度O(n)
class Solution {
public:
vector sortedSquares(vector& nums) {
int leftIndex = 0;
int rightIndex = nums.size() - 1;
vector res(nums.size(), 0);
int k = nums.size() - 1;
while (leftIndex <= rightIndex) {
if (nums[leftIndex] * nums[leftIndex] < nums[rightIndex] * nums[rightIndex]) {
res[k--] = nums[rightIndex] * nums[rightIndex];
rightIndex--;
} else {
res[k--] = nums[leftIndex] * nums[leftIndex];
leftIndex++;
}
}
return res;
}
};
4.长度最小的子数组(209)
- 如果使用两层for循环,则时间复杂度为O(n2)
- 数组中重要方法——滑动窗口(本质上还是通过双指针实现的),需要明确以下三点
- 窗口内是什么(本题窗口是数组和大于等于target的长度最小的子数组)
- 如何移动窗口的起始位置(在本题中,如果当前窗口的值大于s了,则向前移)
- 如果移动窗口的结束位置(本题为遍历数组的指针即for循环中的索引)
// 时间复杂度O(n),因为每个元素在滑动窗口进一次出一次
class Solution {
public:
int minSubArrayLen(int target, vector& nums) {
int res = INT_MAX;
int left = 0;
int sum = 0;
for (int right = 0; right < nums.size(); right++) {
sum += nums[right];
while (sum >= target) {
int subLen = right - left + 1;
res = res < subLen ? res : subLen;
sum -= nums[left++];
}
}
return res == INT_MAX ? 0 : res;
}
};
5.螺旋矩阵II(59)
直接模拟,注意循环不变原则
class Solution {
public:
vector> generateMatrix(int n) {
vector> res(n, vector(n, 0));
int startX = 0, startY = 0;
int loop = n / 2;
int offset = 1;
int count = 1;
while (loop--) {
int i = startX;
int j = startY;
for (; j < n - offset; j++) res[i][j] = count++;
for (; i < n - offset; i++) res[i][j] = count++;
for (; j > startY; j--) res[i][j] = count++;
for (; i > startX; i--) res[i][j] = count++;
startX++;
startY++;
offset++;
}
if (n % 2 != 0) res[n / 2][n / 2] = count;
return res;
}
};
二、链表
- 链表定义:链表是一种通过指针串联在一起的线性结构,每个结点由数据域和指针域(指向下一个结点)组成,因此链表结点在内存中不是连续分布的
- 链表的增添复杂度都为O(1),查询复杂度为O(n);数组的增添复杂度为O(n),查询复杂度为O(1)。
// 链表结构
struct ListNode {
int val;
ListNode* next;
ListNode(int x) : val(x), next(null) {}; // 如果不写构造函数,c++会默认生成一个无参初始化
}
1.移除链表元素(203)
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* removeElements(ListNode* head, int val) {
ListNode* dummy_head = new ListNode(0);
dummy_head->next = head;
ListNode* cur = dummy_head;
while (cur->next) {
if (cur->next->val == val) {
ListNode* temp = cur->next;
cur->next = temp->next;
delete(temp);
} else cur = cur->next; // 注意是else后的cur=cur->next,而不是每次都是cur=cur->next
}
head = dummy_head->next;
delete(dummy_head);
return head;
}
};
2.设计链表(707)
// 注意首先定义链表结构体,之后再定义虚拟头节点和长度的成员属性。
class MyLinkedList {
public:
struct ListNode {
int val;
ListNode* next;
ListNode(int x) : val(x), next(NULL) {};
};
MyLinkedList() {
_dummyHead = new ListNode(0);
_size = 0;
}
int get(int index) {
if (index < 0 || index > _size - 1) return -1;
ListNode* cur = _dummyHead;
while (index--) cur = cur->next; // 利用index--方法比引如count方法简单,循环了index次
return cur->next->val;
}
void addAtHead(int val) {
ListNode* temp = new ListNode(val);
temp->next = _dummyHead->next;
_dummyHead->next = temp;
_size++;
}
void addAtTail(int val) {
addAtIndex(_size, val);
}
void addAtIndex(int index, int val) {
if (index > _size) return ;
else if (index < 0) addAtHead(val);
else {
ListNode* cur = _dummyHead;
while (index--) cur = cur->next;
ListNode* temp1 = cur->next;
ListNode* temp2 = new ListNode(val);
cur->next = temp2;
temp2->next = temp1;
}
_size++;
}
void deleteAtIndex(int index) {
if (index >= _size || index < 0) return;
else {
ListNode* cur = _dummyHead;
while (index--) cur = cur->next;
ListNode* temp = cur->next;
cur->next = temp->next;
delete(temp);
_size--;
}
}
private:
ListNode* _dummyHead;
int _size;
};
/**
* Your MyLinkedList object will be instantiated and called as such:
* MyLinkedList* obj = new MyLinkedList();
* int param_1 = obj->get(index);
* obj->addAtHead(val);
* obj->addAtTail(val);
* obj->addAtIndex(index,val);
* obj->deleteAtIndex(index);
*/
3.反转链表(206)
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* cur = head;
ListNode* pre = NULL;
while (cur) {
// 逻辑顺序:先保存cur->next(temp),再将cur->next指向pre,pre指向cur,cur指向temp
ListNode* temp = cur->next;
cur->next = pre;
pre = cur;
cur = temp;
}
return pre;
}
};
4.两两交换链表中的节点(24)
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
ListNode* dummyHead = new ListNode(0);
dummyHead->next = head;
ListNode* cur = dummyHead;
while (cur->next && cur->next->next) { // 先保证cur->next不为空,再保证cur->next->next不为空
ListNode* temp1 = cur->next;
ListNode* temp2 = cur->next->next->next;
cur->next = cur->next->next;
cur->next->next = temp1;
cur->next->next->next = temp2;
cur = cur->next->next;
}
return dummyHead->next;
}
};
5.删除链表的倒数第N个节点(19)
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* dummyHead = new ListNode(0);
dummyHead->next = head;
ListNode* fast = dummyHead;
ListNode* slow = dummyHead;
while (n--) fast = fast->next;
while (fast->next) {
fast = fast->next;
slow = slow->next;
}
ListNode* temp = slow->next;
slow->next = temp->next;
delete(temp);
return dummyHead->next;
}
};
6.链表相交(160)
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode* curA = headA;
ListNode* curB = headB;
int numA = 0, numB = 0;
while (curA) {
curA = curA->next;
numA++;
}
while (curB) {
curB = curB->next;
numB++;
}
if (numA < numB) {
swap(numA, numB);
swap(headA, headB);
}
int numA_B = numA - numB;
while (numA_B--) headA = headA->next;
while (headA) {
if (headA == headB) return headA;
headA = headA->next;
headB = headB->next;
}
return NULL;
}
};
7.环形链表II(142)
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode* curA = head;
ListNode* curB = head;
while (curB && curB->next) {
curA = curA->next;
curB = curB->next->next;
if (curA == curB) break;
}
if (curB == NULL || curB->next == NULL) return NULL;
curA = head;
while (curA != curB) {
curA = curA->next;
curB = curB->next;
}
return curA;
}
};
三、哈希表
- 哈希表:根据关键码(如数组下标索引)的值而直接进行访问的数据结构。
- 哈希函数:通过hashCode将其他类型的关键码转换为数值(数组的下标)
- 哈希碰撞:不同的关键码映射到同一个下标。解决方法:拉链法(冲突的元素存储在链表中)、线性探索法(前提是哈希表的大小大于数据大小)
- 常见的哈希结构:数组、set(集合)、map(映射)
- 当我们需要查询一个元素是否出现过,或者一个元素是否在集合里的时候,就要第一时间想到哈希法。
1.有效的字母异位词(242)
class Solution {
public:
bool isAnagram(string s, string t) {
int hash[26] = {0};
for (auto s0 : s) hash[s0 - 'a']++;
for (auto t0 : t) hash[t0 - 'a']--;
for (int i = 0; i < 26; i++) {
if (hash[i] != 0) return false;
}
return true;
}
};
2.两个数组的交集(349)
// 1.利用容器可以创建集合
// 2.集合有find、insert成员函数,find返回的是迭代器
// 3.利用集合可以转为容器
class Solution {
public:
vector intersection(vector& nums1, vector& nums2) {
unordered_set uset(nums1.begin(), nums1.end());
unordered_set result;
for (int n : nums2) {
if (uset.find(n) != uset.end()) result.insert(n);
}
return vector(result.begin(), result.end());
}
};
3.快乐数(202)
// 1.注意怎么求和
// 2.当出现重复和时会导致无限循环,而哈希表可以检测重复
class Solution {
public:
bool isHappy(int n) {
unordered_set uset;
while (1) {
int sum = getNum(n);
if (sum == 1) return true;
if (uset.find(getNum(n)) != uset.end()) return false;
else {
uset.insert(n);
n = sum;
}
}
}
int getNum(int n) {
int sum = 0;
int num = 0;
while (n) {
num = n % 10;
n /= 10;
sum += num * num;
}
return sum;
}
};
4.两数之和(1)
// 1.同时需要记录数组值和下标时可以用映射,map结构为,其中数组值作为key,数组下标作为val
// 2.map调用find时查找的时key
// 3.map中元素可以用迭代器来访问。iter->first访问的是key,iter->second访问的是val
// 4.map插入元素用pair来表示插入数据的结构
class Solution {
public:
vector twoSum(vector& nums, int target) {
unordered_map umap;
for (int i = 0; i < nums.size(); i++) {
auto iter = umap.find(target - nums[i]);
if (iter == umap.end()) umap.insert(pair(nums[i], i));
else return {i, iter->second};
}
return {}; // 不报错
}
};
5.四数相加II(454)
// map[元素值]以元素值提取元素
class Solution {
public:
int fourSumCount(vector& nums1, vector& nums2, vector& nums3, vector& nums4) {
unordered_map umap;
for (auto n1 : nums1) {
for (auto n2 : nums2) {
umap[n1 + n2]++;
}
}
int res = 0;
for (auto n3 : nums3) {
for (auto n4 : nums4) {
if (umap.find(-n3 - n4) != umap.end()) res += umap[-n3 - n4];
}
}
return res;
}
};
6.赎金信(383)
// 已知长度的数组最好用普通数组
class Solution {
public:
bool canConstruct(string ransomNote, string magazine) {
int hash[26] = {0};
for (auto m : magazine) hash[m - 'a']++;
for (auto r : ransomNote) {
if (hash[r - 'a'] == 0) return false;
hash[r - 'a']--;
}
return true;
}
};
7.三数之和(15)
// 用哈希表不方便剪枝,采用三指针法,有i、left、right
class Solution {
public:
vector> threeSum(vector& nums) {
sort(nums.begin(), nums.end());
vector> res;
for (int i = 0; i < nums.size(); i++) {
if (i > 0 && nums[i - 1] == nums[i]) continue;
int left = i + 1;
int right = nums.size() - 1;
while (left < right) {
if (nums[i] + nums[left] + nums[right] < 0) left++;
else if (nums[i] + nums[left] + nums[right] > 0) right--;
else {
res.push_back({nums[i], nums[left], nums[right]});
while (left < right && nums[left] == nums[left + 1]) left++;
while (left < right && nums[right] == nums[right - 1]) right--;
left++;
right--;
}
}
}
return res;
}
};
8.四数之和(18)
// 思路与三数之和相同只是增加了一层for循环
class Solution {
public:
vector> fourSum(vector& nums, int target) {
sort(nums.begin(), nums.end());
vector> res;
for (int k = 0; k < nums.size(); k++) {
if (k > 0 && nums[k] == nums[k - 1]) continue;
for (int i = k + 1; i < nums.size(); i++) {
if (i > k + 1 && nums[i] == nums[i - 1]) continue;
int left = i + 1;
int right = nums.size() - 1;
while (left < right) {
if ((long)nums[k] + nums[i] + nums[left] + nums[right] < target) left++;
else if ((long)nums[k] + nums[i] + nums[left] + nums[right] > target) right--;
else {
res.push_back({nums[k], nums[i], nums[left], nums[right]});
while (left < right && nums[left] == nums[left + 1]) left++;
while (left < right && nums[right] == nums[right - 1]) right--;
left++;
right--;
}
}
}
}
return res;
}
};
四、 字符串
1.反转字符串(344)
// 最好不要用reverse,可以用swap
class Solution {
public:
void reverseString(vector& s) {
int left = 0;
int right = s.size() - 1;
while (left < right) {
char temp = s[left];
s[left] = s[right];
s[right] = temp;
left++;
right--;
}
}
};
2.反转字符串II(541)
// 可以用reverse函数
class Solution {
public:
string reverseStr(string s, int k) {
for (int i = 0; i < s.size(); i += 2 * k) {
if ((s.size() - i) < k) reverse(s.begin() + i, s.end());
else reverse(s.begin() + i, s.begin() + i + k);
}
return s;
}
};
3.替换空格(剑指Offer 05)
// 首先将字符串扩容,之后用双指针法从后向前遍历
class Solution {
public:
string replaceSpace(string s) {
int count = 0;
for (int i = 0; i < s.size(); i++) {
if (s[i] == ' ') count++;
}
int k = s.size() - 1;
s.resize(s.size() + 2 * count);
for (int i = s.size() - 1; i >= 0; i--) {
if (s[k] != ' ') s[i] = s[k--];
else {
s[i--] = '0';
s[i--] = '2';
s[i] = '%';
k--;
}
}
return s;
}
};
4.反转字符串中的单词(151)
// 三步走:去除多余空格->反转整个字符串->反转每个单词
class Solution {
public:
string reverseWords(string s) {
int slow = 0;
for (int i = 0; i < s.size(); i++) {
if (s[i] != ' ') {
while (i < s.size() && s[i] != ' ') s[slow++] = s[i++];
s[slow++] = ' ';
}
}
s.resize(slow - 1); // 多加了一个末尾空格
reverse(s.begin(), s.end());
int start = 0;
for (int i = 0; i <= s.size(); i++) {
if (s[i] == ' ' || i == s.size()) {
reverse(s.begin() + start, s.begin() + i);
start = i + 1;
}
}
return s;
}
};
};
5.左旋转字符串(剑指Offer58-II)
class Solution {
public:
string reverseLeftWords(string s, int n) {
reverse(s.begin(), s.begin() + n);
reverse(s.begin() + n, s.end());
reverse(s.begin(), s.end());
return s;
}
};
6.找出字符串中第一个匹配项的下标(28)
// 使用KMP算法求解
// 1.主要思想:当字符串不匹配时,可以知道一部分之前已经匹配的文本内容,可以利用这些信息避免从头匹配
// 2.前缀表的定义:记录下标i之前(包括i)的字符串中,有多大长度的相同前缀后缀,其中前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串,后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串
// 3.next数组可以与前缀表相同,也可以是前缀表中所有元素值减一(本题解使用这种方法)
class Solution {
public:
void getNext(int* next, const string& s) {
// 1.初始化
int j = -1; // j指向前缀末尾,i指向后缀末尾
next[0] = j; // next[i]表示以i结尾的最长相同前后缀的长度(即为j)
for (int i = 1; i < s.size(); i++) {
// 2.不匹配情况
while (j >= 0 && s[i] != s[j + 1]) j = next[j]; // 注意用while
// 3.匹配情况
if (s[i] == s[j + 1]) j++;
// 给next[i]赋值
next[i] = j;
}
}
int strStr(string haystack, string needle) {
int next[needle.size()];
getNext(next, needle);
int j = -1;
for (int i = 0; i < haystack.size(); i++) {
while (j >= 0 && haystack[i] != needle[j + 1]) j = next[j];
if (haystack[i] == needle[j + 1]) j++;
if (j == needle.size() - 1) return (i - needle.size() + 1); // 注意要减1
}
return -1;
}
};
7.重复的子字符串(459)
// 使用KMP方法求解,如果数组长度能够整除最长相同前后缀则说明该字符串由重复子字符串构成
class Solution {
public:
void getNext(int* next, const string& s) {
int j = -1;
next[0] = j;
for (int i = 1; i < s.size(); i++) {
while (j >= 0 && s[i] != s[j + 1]) j = next[i];
if (s[i] == s[j + 1]) j++;
next[i] = j;
}
}
bool repeatedSubstringPattern(string s) {
int next[s.size()];
getNext(next, s);
int len = s.size();
if (next[len - 1] != -1 && len % (len - (next[len - 1] + 1)) == 0) return true;
return false;
}
};
五、栈与队列
- 栈是先进后出,队列是先进先出
- 栈和队列不是容器,而是容器适配器,在内存中不是连续分布的,底层默认用双端队列deque实现(也可指定vector、list实现)
- 栈和队列没有迭代器,目前我们所说的stack和queue是SGI STL
1.用栈实现队列(232)
// push向st1 push,pop和peek需要向st2转移,转移完成之后再转移回st1
// c++ stl中的stack有push、pop、size、top、empty
class MyQueue {
public:
stack st1;
stack st2;
MyQueue() {
}
void push(int x) {
st1.push(x);
}
int pop() {
while (!st1.empty()) {
st2.push(st1.top());
st1.pop();
}
int res = st2.top();
st2.pop();
while (!st2.empty()) {
st1.push(st2.top());
st2.pop();
}
return res;
}
int peek() {
while (!st1.empty()) {
st2.push(st1.top());
st1.pop();
}
int res = st2.top();
while (!st2.empty()) {
st1.push(st2.top());
st2.pop();
}
return res;
}
bool empty() {
return st1.empty();
}
};
/**
* Your MyQueue object will be instantiated and called as such:
* MyQueue* obj = new MyQueue();
* obj->push(x);
* int param_2 = obj->pop();
* int param_3 = obj->peek();
* bool param_4 = obj->empty();
*/
2.用队列实现栈(255)
// push向que1 push,pop和top需要向que2转移,转移完成之后再转移回que1
// c++ stl中的queue有push、pop、size、front、empty
class MyStack {
public:
queue que1;
queue que2;
MyStack() {
}
void push(int x) {
que1.push(x);
}
int pop() {
int len = que1.size() - 1;
while (len--) {
que2.push(que1.front());
que1.pop();
}
int res = que1.front();
que1.pop();
while (!que2.empty()) {
que1.push(que2.front());
que2.pop();
}
return res;
}
int top() {
int len = que1.size() - 1;
while (len--) {
que2.push(que1.front());
que1.pop();
}
int res = que1.front();
que2.push(res);
que1.pop();
while (!que2.empty()) {
que1.push(que2.front());
que2.pop();
}
return res;
}
bool empty() {
return que1.empty();
}
};
/**
* Your MyStack object will be instantiated and called as such:
* MyStack* obj = new MyStack();
* obj->push(x);
* int param_2 = obj->pop();
* int param_3 = obj->top();
* bool param_4 = obj->empty();
*/
3.有效的括号(20)
// 遇到左括号进栈,遇到右括号出栈
class Solution {
public:
bool isValid(string s) {
stack st;
for (auto c : s) {
if (c == '(' || c == '[' || c == '{' ) st.push(c);
else {
if (!st.empty() && ((st.top() == '(' && c == ')') || (st.top() == '[' && c == ']') || (st.top() == '{' && c == '}'))) st.pop();
else return false;
}
}
if (!st.empty()) return false;
return true;
}
};
4.删除字符串中的所有相邻重复项(1047)
class Solution {
public:
string removeDuplicates(string s) {
stack st;
for (auto c : s) {
if (!st.empty() && st.top() == c) st.pop();
else st.push(c);
}
int len = st.size();
s.resize(len);
if (len == 0) return s;
for (int i = len - 1; i >= 0; i--) {
s[i] = st.top();
st.pop();
}
return s;
}
};
5.逆波兰表达式求值(150)
// vector也可用范围for循环,string变为int可以用stoi函数,乘法编译不过去可以将num改为long类型
class Solution {
public:
int evalRPN(vector& tokens) {
stack st;
for (auto s : tokens) {
if (s != "+" && s != "-" && s != "*" && s != "/") st.push(stoi(s));
else {
int num1 = st.top();
st.pop();
int num2 = st.top();
st.pop();
if (s == "+") st.push(num2 + num1);
else if (s == "-") st.push(num2 - num1);
else if (s == "*") st.push(num2 * num1);
else if (s == "/") st.push(num2 / num1);
}
}
return st.top();
}
};
6.滑动窗口最大值(239)
// 1.使用两层for循环会超时
// 2.这里创建了一个新的队列类,该队列类是一个单调队列
// 3.deque是双端队列,有push_front、push_back、pop_front、pop_back、front、back、empty函数
//
class Solution {
public:
class MyQue {
public:
deque deq;
void pop(int val) {
if (!deq.empty() && val == deq.front()) deq.pop_front(); // 用if
}
void push(int val) {
while (!deq.empty() && val > deq.back()) deq.pop_back(); // 用while
deq.push_back(val);
}
int front() {
return deq.front();
}
};
vector maxSlidingWindow(vector& nums, int k) {
MyQue mq;
vector res;
for (int i = 0; i < k; i++) mq.push(nums[i]);
res.push_back(mq.front());
for (int i = k; i < nums.size(); i++) {
mq.pop(nums[i - k]);
mq.push(nums[i]);
res.push_back(mq.front());
}
return res;
}
};
7.前K个高频元素(347)
// 核心是优先级队列,分三步走
// 1.利用map统计元素出现的频率
// 2.利用priority_queue(优先级队列,本质是堆,是一棵完全二叉树,缺省时为大顶堆)进行小顶堆排序,priority_queue, 其中Type为数据类型,Container为容器(必须为vector),Functional比较方式(less表示大顶堆,greater表示小顶堆;自己写的小于也是大顶堆,大于是小顶堆;但注意在写快排的时候left>right是从大到小)
// 3.提取前K个高频元素
// 优先级队列排序的时间复杂度为O(log n)
class Solution {
public:
class cmp {
public:
bool operator()(pair& lhs, pair rhs) {
return lhs.second > rhs.second;
}
};
vector topKFrequent(vector& nums, int k) {
unordered_map umap;
for (auto n : nums) umap[n]++;
priority_queue, vector>, cmp> pq;
for (auto it = umap.begin(); it != umap.end(); it++) {
pq.push(*it);
if (pq.size() > k) pq.pop();
}
vector res(k, 0);
for (int i = k - 1; i >= 0; i--) {
res[i] = pq.top().first; // 优先级队列即小顶堆的堆顶用top,而非front
pq.pop();
}
return res;
}
};
六、二叉树
- 定义
- 满二叉树:只有度为0的结点和度为2的结点,并且度为0的结点在同一层上
- 完全二叉树:除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。(优先级队列即堆是一棵完全二叉树)
- 二叉搜索树:有序树,若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;它的左、右子树也分别为二叉搜索树
- 平衡二叉树:左子树和右子树的高度之差的绝对值小于等于1;左子树和右子树也是平衡二叉树。
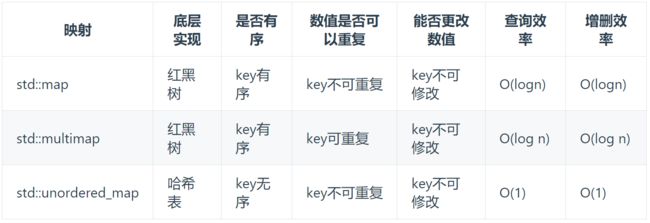
- C++中map、set、multiset、multimap底层都是平衡二叉搜索树(红黑树),增删的时间复杂度为O(log n)
- 结构
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
- 遍历
- 深度优先遍历:先往深走,遇到叶子结点再往回走;有前序、中序、后序遍历(迭代法、递归法)
- 中间结点的顺序即为遍历方式(前序遍历:中左右,中序遍历:左中右,后续遍历:左右中)
- 广度优先遍历:一层一层遍历;有层序遍历(迭代法)
- 递归法结构(每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中,递归返回的时候,从栈顶弹出上一次递归的各项参数)
- 确定递归函数的参数和返回值:确定哪些参数是递归的过程中需要处理的,那么舅在递归函数里加上这个参数,并明确每次递归的返回值是什么进而确定递归函数的返回类型。
- 确定终止条件:如果终止条件没写或写的不对,会遇到栈溢出的错误(os通过栈保存每一层递归信息)
- 确定单层递归逻辑:这里会重复调用自己来实现递归过程。
- 迭代结构:用栈实现
1.二叉树的前序遍历(144)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void traversal(TreeNode* cur, vector& vec) {
if (cur == NULL) return ;
vec.push_back(cur->val);
traversal(cur->left, vec);
traversal(cur->right, vec);
}
vector preorderTraversal(TreeNode* root) {
vector vec;
traversal(root, vec);
return vec;
}
};
// 迭代实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector preorderTraversal(TreeNode* root) {
vector res;
stack st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
st.pop();
res.push_back(node->val);
if (node->right) st.push(node->right); // 注意是node而不是root!!!!
if (node->left) st.push(node->left);
}
return res;
}
};
2.二叉树的中遍历(94)
// 递归实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void traversal(TreeNode* cur, vector& vec) {
if (cur == NULL) return ;
traversal(cur->left, vec);
vec.push_back(cur->val);
traversal(cur->right, vec);
}
vector inorderTraversal(TreeNode* root) {
vector result;
traversal(root, result);
return result;
}
};
// 迭代实现(由于访问从中间结点开始,但处理从左边结点开始,访问顺序和处理顺序很不一样),只有中序遍历的迭代法公式不一样
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector inorderTraversal(TreeNode* root) {
vector res;
stack st;
TreeNode* cur = root;
while (cur != NULL || !st.empty()) {
if (cur != NULL) {
st.push(cur);
cur = cur->left;
} else {
cur = st.top();
st.pop();
res.push_back(cur->val);
cur = cur->right;
}
}
return res;
}
};
3.二叉树的后序遍历(145)
// 递归实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void traversal(TreeNode* cur, vector& vec) {
if (cur == NULL) return ;
traversal(cur->left, vec);
traversal(cur->right, vec);
vec.push_back(cur->val);
}
vector postorderTraversal(TreeNode* root) {
vector result;
traversal(root, result);
return result;
}
};
// 迭代实现(和前序遍历的迭代法类似)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector postorderTraversal(TreeNode* root) {
stack st;
vector res;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
st.pop();
res.push_back(node->val);
if (node->left) st.push(node->left);
if (node->right) st.push(node->right);
}
reverse(res.begin(), res.end());
return res;
}
};
4.二叉树的层序遍历(102)
// 队列先进先出,符合一层一层遍历的逻辑,栈先进先出适合模拟深度优先遍历即递归的逻辑
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector> levelOrder(TreeNode* root) {
vector> res;
queue que;
if (root != NULL) que.push(root);
while (!que.empty()) {
int size = que.size();
vector vec;
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
vec.push_back(node->val);
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
res.push_back(vec);
}
return res;
}
};
5.翻转二叉树(226)
// 递归实现(前序遍历)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* traversal(TreeNode* root) {
if (root == NULL) return NULL;
swap(root->left, root->right);
traversal(root->left);
traversal(root->right);
return root;
}
TreeNode* invertTree(TreeNode* root) {
return traversal(root);
}
};
// 迭代实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
stack st;
if (root == NULL) return root;
st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
st.pop();
swap(node->left, node->right);
if (node->right) st.push(node->right);
if (node->left) st.push(node->left);
}
return root;
}
};
6.对称二叉树(101)
// 后序遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool traversal(TreeNode* left, TreeNode* right) {
if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
else if (left->val != right->val) return false;
bool cmp1 = traversal(left->left, right->right);
bool cmp2 = traversal(left->right, right->left);
return cmp1 && cmp2;
}
bool isSymmetric(TreeNode* root) {
return traversal(root->left, root->right);
}
};
7.二叉树的最大深度(104)
- 二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数或者节点数(力扣用节点数表示)
- 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数或者节点数(力扣用节点数表示)
- 使用前序求的就是深度,使用后序求的是高度
- 根结点的高度就是二叉树的最大深度,所以使用后序遍历求根结点高度
// 后序遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int traversal(TreeNode* root) {
if (root == NULL) return 0;
int left = traversal(root->left);
int right = traversal(root->right);
return max(left, right) + 1;
}
int maxDepth(TreeNode* root) {
return traversal(root);
}
};
// 层序遍历(迭代法)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode* root) {
queue que;
if (root != NULL) que.push(root);
int res = 0;
while (!que.empty()) {
int size = que.size();
res++;
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
}
return res;
}
};
8.二叉树的最小深度(111)
// 后序遍历,与求最大深度不同,因为只有当左右结点为空时才是叶子结点
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int traversal(TreeNode* root) {
if (root == NULL) return 0;
int left = traversal(root->left);
int right = traversal(root->right);
if (root->left == NULL && root->right != NULL) return right + 1;
if (root->right == NULL && root->left != NULL) return left + 1;
return min(left, right) + 1;
}
int minDepth(TreeNode* root) {
return traversal(root);
}
};
9.完全二叉树的节点个数(222)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int getNum(TreeNode* root) {
if (root == NULL) return 0;
int l = getNum(root->left);
int r = getNum(root->right);
return 1 + l + r;
}
int countNodes(TreeNode* root) {
return getNum(root);
}
};
10.平衡二叉树(110)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int traversal(TreeNode* root) {
if (root == NULL) return 0;
int left = traversal(root->left);
if (left == -1) return -1;
int right = traversal(root->right);
if (right == -1) return -1;
return abs(left - right) <= 1 ? max(left, right) + 1 : -1;
}
bool isBalanced(TreeNode* root) {
return traversal(root) == -1 ? false : true;
}
};
11.二叉树的所有路径(257)
// 回溯和递归是一一对应的,有一个递归就有一个回溯
// 强制类型转化:整型->字符串:to_string,字符串->整型:stoi
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void getPath(TreeNode* root, vector& vec, vector& res) {
vec.push_back(root->val);
if (root->left == NULL && root->right == NULL) {
string sPath;
for (int i = 0; i < vec.size() - 1; i++) {
sPath += to_string(vec[i]);
sPath += "->";
}
sPath += to_string(vec[vec.size() - 1]);
res.push_back(sPath);
}
if (root->left) {
getPath(root->left, vec, res);
vec.pop_back();
}
if (root->right) {
getPath(root->right, vec, res);
vec.pop_back();
}
}
vector binaryTreePaths(TreeNode* root) {
vector res;
vector vec;
getPath(root, vec, res);
return res;
}
};
12.左叶子之和(404)
// 后序遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int getLeftSum(TreeNode* root) {
if (root == NULL) return 0;
int left = getLeftSum(root->left);
if (root->left != NULL && root->left->left == NULL && root->left->right == NULL) left = root->left->val;
int right = getLeftSum(root->right);
return left + right;
}
int sumOfLeftLeaves(TreeNode* root) {
return getLeftSum(root);
}
};
13.找树左下角的值(513)
// 前序/中序/后序遍历都可以
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int res;
int maxDepth = INT_MIN;
void getLeft(TreeNode* root, int depth) { // 这里是拷贝赋值,并不是引用传递
if (root->left == NULL && root->right == NULL) {
if (depth > maxDepth) {
maxDepth = depth;
res = root->val;
}
return;
}
if (root->left) getLeft(root->left, depth + 1);
if (root->right) getLeft(root->right, depth + 1);
}
int findBottomLeftValue(TreeNode* root) {
getLeft(root, 0);
return res;
}
};
// 层序遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int findBottomLeftValue(TreeNode* root) {
queue que;
if (root != NULL) que.push(root);
int res;
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
if (i == 0) res = node->val;
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
}
return res;
}
};
14.路径总和(112)
递归函数什么时候需要返回值
- 如果需要搜索整棵二叉树且不用递归处理返回值,则递归不需要返回值
- 如果需要搜索二叉树且需要处理递归返回值,则递归函数需要返回值
- 如果搜索某一条符合条件的路径,则递归需要返回值
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool getPath(TreeNode* root,int targetSum) {
if (root->left == NULL && root->right == NULL && targetSum == 0) return true;
if (root->left == NULL && root->right == NULL) return false;
if (root->left) {
if (getPath(root->left, targetSum - root->left->val)) return true;
}
if (root->right) {
if (getPath(root->right, targetSum - root->right->val)) return true;
}
return false;
}
bool hasPathSum(TreeNode* root, int targetSum) {
if (root == NULL) return false;
return getPath(root, targetSum - root->val);
}
};
15.从中序与后序遍历序列构造二叉树(106)
利用前序数组和中序数组可以确定一棵二叉树(前序数组的第一个元素切割中序数组)
利用中序数组和后序数组也可确定一棵二叉树(后序数组的最后一个元素切割中序数组)
但前序数组和后序数组不能确定一棵二叉树
// 利用后序数组切割中序数组
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* build(vector& inorder, vector& postorder) {
if (postorder.size() == 0) return NULL;
// 1.取出后序数组最后一个元素
int rootVal = postorder[postorder.size() - 1];
TreeNode* root = new TreeNode(rootVal);
// 如果后序数组只有一个元素了,则直接返回
if (postorder.size() == 1) return root;
// 2.寻找分割点
int delimiter = 0;
for (; delimiter < inorder.size(); delimiter++) {
if (inorder[delimiter] == rootVal) break;
}
// 3.分割中序数组
vector leftInorder(inorder.begin(), inorder.begin() + delimiter);
vector rightInorder(inorder.begin() + delimiter + 1, inorder.end());
// 4.分割后序数组
vector leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
vector rightPostorder(postorder.begin() + leftInorder.size(), postorder.end() - 1);
// 5.递归赋值
root->left = build(leftInorder, leftPostorder);
root->right = build(rightInorder, rightPostorder);
return root;
}
TreeNode* buildTree(vector& inorder, vector& postorder) {
return build(inorder, postorder);
}
};
16.最大二叉树(654)
一般情况来说:如果让空节点(空指针)进入递归,就不加if,如果不让空节点进入递归,就加if限制一下, 终止条件也会相应的调整。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* traversal(vector& nums, int left, int right) {
if (left >= right) return NULL;
// 寻找最大值的下标
int maxIndex = left;
for (int i = maxIndex + 1; i < right; i++) {
if (nums[i] > nums[maxIndex]) maxIndex = i;
}
// 赋值
TreeNode* root = new TreeNode(nums[maxIndex]);
root->left = traversal(nums, left, maxIndex);
root->right = traversal(nums, maxIndex + 1, right);
return root;
}
TreeNode* constructMaximumBinaryTree(vector& nums) {
return traversal(nums, 0, nums.size());
}
};
17.合并二叉树(617)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* build(TreeNode* root1, TreeNode* root2) {
if (root1 == NULL) return root2;
if (root2 == NULL) return root1;
root1->val += root2->val;
root1->left = build(root1->left, root2->left);
root1->right = build(root1->right, root2->right);
return root1;
}
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
return build(root1, root2);
}
};
18.二叉搜索树中的搜索(700)
二叉搜索树一般采用中序遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* traversal(TreeNode* root, int val) {
if (root == NULL || root->val == val) return root;
TreeNode* res = NULL;
if (root->val > val) res = traversal(root->left, val);
if (root->val < val) res = traversal(root->right, val);
return res;
}
TreeNode* searchBST(TreeNode* root, int val) {
return traversal(root, val);
}
};
19.验证二叉搜索树(98)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
long maxVal = LONG_MIN;
bool BST(TreeNode* root) {
if (root == NULL) return true;
bool left = BST(root->left);
if (maxVal < root->val) maxVal = root->val;
else return false;
bool right = BST(root->right);
return left && right;
}
bool isValidBST(TreeNode* root) {
return BST(root);
}
};
20.二叉搜索树的最小绝对差(530)
- 在二叉树中通过两个前后指针作比较,会经常用到
// 定义一个结点指向前一个结点
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int minVal = INT_MAX;
TreeNode* pre = NULL;
void traversal(TreeNode* root) {
if (root == NULL) return ;
traversal(root->left);
if (pre != NULL) minVal = min(minVal, root->val - pre->val);
pre = root;
traversal(root->right);
return ;
}
int getMinimumDifference(TreeNode* root) {
traversal(root);
return minVal;
}
};
21.二叉搜索树中的众数(501)
// 同样定义一个结点指向前一个结点
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int maxVal = 0;
int count = 0;
vector res;
TreeNode* pre = NULL;
void traversal(TreeNode* root) {
if (root == NULL) return;
traversal(root->left);
if (pre == NULL) count = 1;
else if (pre->val == root->val) count++;
else count = 1;
if (count == maxVal) res.push_back(root->val);
if (count > maxVal) {
maxVal = count;
res.clear();
res.push_back(root->val);
}
pre = root;
traversal(root->right);
}
vector findMode(TreeNode* root) {
traversal(root);
return res;
}
};
22.二叉树的最近公共祖先(236)
- 后序遍历是天然的回溯
- 在递归函数有返回值的情况下:如果要搜索一条边,递归函数返回值不为空的时候立刻返回;如果搜索整个树,直接用left、right接住返回值,left和right后序还需要处理逻辑,也就是后序遍历中处理中间结点的逻辑(即回溯)。综上,只要是处理逻辑的就需要遍历整棵树。
// 如果递归函数有返回值,搜索一条边
if (递归函数(root->left)) return ;
if (递归函数(root->right)) return ;
// 如果递归函数有返回值,搜索整个树
left = 递归函数(root->left);
right = 递归函数(root->right);
left与right的逻辑处理;
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* traversal(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == p || root == q || root == NULL) return root;
TreeNode* left = traversal(root->left, p, q);
TreeNode* right = traversal(root->right, p, q);
if (left != NULL && right != NULL) return root;
else if (left == NULL && right != NULL) return right;
else if (left != NULL && right == NULL) return left;
else return NULL;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
return traversal(root, p, q);
}
};
总结:
平衡二叉搜索树是平衡二叉树和二叉搜索树的组合
平衡二叉树与完全二叉树的区别在底层结点,完全二叉树底层必须是从做到右连续且次底层是满的,完全二叉树一定是平衡二叉树
堆是一棵完全二叉树,但堆不是二叉搜索树
23.二叉搜索树的公共祖先(235)
// 利用二叉搜索树的特点,当root结点再[p, q]之间则说明该结点是公共祖先
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* traversal(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == NULL) return NULL;
if (root->val > p->val && root->val > q->val) return traversal(root->left, p, q);
else if (root->val < q->val && root->val < p->val) return traversal(root->right, p, q);
else return root;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
return traversal(root, p, q);
}
};
24.二叉搜索树中的插入操作(701)
// 遇到空结点就插入,遍历顺序由插入的值决定
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* traversal(TreeNode* root, int val) {
if (root == NULL) {
TreeNode* node = new TreeNode(val);
return node;
}
if (root->val > val) root->left = traversal(root->left, val);
if (root->val < val) root->right = traversal(root->right, val);
return root;
}
TreeNode* insertIntoBST(TreeNode* root, int val) {
return traversal(root, val);
}
};
25.删除二叉搜索树中的结点(450)
/* 第一种情况:没找到删除的节点,遍历到空节点直接返回了
找到删除的节点
第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
第三种情况:删除节点的左孩子为空,右孩子不为空,删除节点,右孩子补位,返回右孩子为根节点
第四种情况:删除节点的右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点
第五种情况:左右孩子节点都不为空,则将删除节点的左子树头结点(左孩子)放到删除节点的右子树的最左面节点的左孩子上,返回删除节点右孩子为新的根节点。
*/
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* del(TreeNode* root, int key) {
if (root == NULL) return root;
if (root->val == key) {
if (root->left == NULL) return root->right;
else if (root->right == NULL) return root->left;
else {
TreeNode* cur = root->right;
while (cur->left != NULL) cur = cur->left;
cur->left = root->left;
root = root->right;
return root;
}
}
if (root->val > key) root->left = del(root->left, key);
if (root->val < key) root->right = del(root->right, key);
return root;
}
TreeNode* deleteNode(TreeNode* root, int key) {
return del(root, key);
}
};
26.修剪二叉搜索树(669)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* traversal(TreeNode* root, int low, int high) {
if (root == NULL) return root;
if (root->val < low) return traversal(root->right, low, high);
if (root->val > high) return traversal(root->left, low, high);
root->left = traversal(root->left, low, high);
root->right = traversal(root->right, low, high);
return root;
}
TreeNode* trimBST(TreeNode* root, int low, int high) {
return traversal(root, low, high);
}
};
27.将有序数组转换为二叉搜索树(108)
// 注意区间
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* traversal(vector& nums, int left, int right) {
if (left > right) return NULL;
int mid = left + (right - left) / 2;
TreeNode* root = new TreeNode(nums[mid]);
root->left = traversal(nums, left, mid - 1);
root->right = traversal(nums, mid + 1, right);
return root;
}
TreeNode* sortedArrayToBST(vector& nums) {
return traversal(nums, 0, nums.size() - 1);
}
};
28.把二叉搜索树转换为累加树(538)
// 反中序遍历累加
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int pre = 0;
void traversal(TreeNode* root) {
if (root == NULL) return ;
traversal(root->right);
root->val += pre;
pre = root->val;
traversal(root->left);
}
TreeNode* convertBST(TreeNode* root) {
traversal(root);
return root;
}
};
- 涉及到二叉树的构造,无论普通二叉树还是二叉搜索树一定前序,都是先构造中节点。
- 求普通二叉树的属性,一般是后序,一般要通过递归函数的返回值做计算。
- 求二叉搜索树的属性,一定是中序了,要不白瞎了有序性了。
七、回溯
- 回溯是递归的副产品,有递归就会有回溯,回溯的本质是穷举
- 回溯需要解决的问题
- 组合问题:N个数里面按一定规则找出k个数的集合(组合无序)
- 切割问题:一个字符串按一定规则有几种切割方式
- 排列问题:N个数按一定规则全排列,有几种排列方式(排列有序)
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 棋盘问题:N皇后,解数独等等
- 回溯三部曲(和递归类似)
- 回溯函数的返回值和参数:返回值一般是void,函数名字为backtracking,参数不容易一次确定,所以先写逻辑,再写参数
- 回溯的终止条件:一般到叶子结点就找到了满足条件的一条答案,把答案存放起来,并结束本层递归
- 回溯遍历的过程:回溯一般在集合中递归搜索,集合的大小构成了树的宽度,递归的深度构成了树的深度,即for循环是横向遍历,backtracking是纵向遍历
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择本层集合中的元素(树中结点孩子的数量就是集合的大小)) {
处理结点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果;
}
}
1.组合(77)
class Solution {
public:
vector> res;
void backtracking(int n, int k, int start, vector& vec) {
if (vec.size() == k) {
res.push_back(vec);
return;
}
// 此处可以做剪枝优化:i < n - (k - vec.size() + 1)
for (int i = start; i <= n; i++) {
vec.push_back(i);
backtracking(n, k, i + 1, vec); // 下一层搜索从i+1开始,而不是start+1
vec.pop_back();
}
}
vector> combine(int n, int k) {
vector vec;
backtracking(n, k, 1, vec);
return res;
}
};
2.组合总和(216)
class Solution {
public:
vector> res;
vector vec;
void backtracking(int k, int n, int start, int sum) {
if (sum > n) return ;
if (vec.size() == k) {
if (sum == n) res.push_back(vec);
return ;
}
for (int i = start; i <= 9 - (k - vec.size()) + 1; i++) {
vec.push_back(i);
sum += i;
backtracking(k, n, i + 1, sum);
vec.pop_back();
sum -= i;
}
}
vector> combinationSum3(int k, int n) {
backtracking(k, n, 1, 0);
return res;
}
};
3.电话号码的字母组合(17)
class Solution {
public:
const string letter[10] = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
vector res;
string path;
void backtracking(const string& digits, int index) {
if (path.size() == digits.size()) {
res.push_back(path);
return ;
}
string s = letter[digits[index] - '0'];
for (int i = 0; i < s.size(); i++) { // 注意每层循环都是从0开始
path.push_back(s[i]); // string有push_back和pop_back()函数
backtracking(digits, index + 1); // 递归条件是index加1而不是i+1
path.pop_back();
}
}
vector letterCombinations(string digits) {
if (digits.size() == 0) return res; // 测试案例有空值
backtracking(digits, 0);
return res;
}
};
4.组合总和(39)
class Solution {
public:
vector> res;
vector vec;
void backtracking(vector& candidates, int target, int start) {
if (target <= 0) {
if (target == 0) res.push_back(vec);
return ;
}
for (int i = start; i < candidates.size(); i++) {
vec.push_back(candidates[i]);
target -= candidates[i];
backtracking(candidates, target, i); // 不是i+1,应为在下一层循环可以从i开始,表示可以重复
vec.pop_back();
target += candidates[i];
}
}
vector> combinationSum(vector& candidates, int target) {
backtracking(candidates, target, 0);
return res;
}
};
5.组合总和II(40)
同一支树可以重复,同一层树不可重复,需要引入新的used变量,used为false时表示同一层
class Solution {
public:
vector> res;
vector vec;
void backtracking(vector& candidates, int target, int start, vector& used) {
if (target <= 0) {
if (target == 0) res.push_back(vec);
return ;
}
for (int i = start; i < candidates.size(); i++) {
if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) continue;
vec.push_back(candidates[i]);
target -= candidates[i];
used[i] = true;
backtracking(candidates, target, i + 1, used);
vec.pop_back();
target += candidates[i];
used[i] = false;
}
}
vector> combinationSum2(vector& candidates, int target) {
sort(candidates.begin(), candidates.end());
vector used(candidates.size(), false); // 第一个参数是大小,第二个参数是值
backtracking(candidates, target, 0, used);
return res;
}
};
6.分割回文串(131)
class Solution {
public:
vector> res;
vector vec;
bool istrue(string s, int start, int end) {
for (int i = start, j = end; i < j; i++, j--) {
if (s[i] != s[j]) return false;
}
return true;
}
void backtracking(string s, int start) {
if (start >= s.size()) {
res.push_back(vec);
return ;
}
for (int i = start; i < s.size(); i++) {
// s.substr(pos, len)函数的返回值是string,包含s中从pos开始的len个字符的拷贝
if (istrue(s, start, i)) vec.push_back(s.substr(start, i - start + 1));
else continue;
backtracking(s, i + 1);
vec.pop_back();
}
}
vector> partition(string s) {
backtracking(s, 0);
return res;
}
};
7.复原IP(93)
class Solution {
public:
bool IPstr(string s, int start, int end) {
if (start > end) return false;
if (start != end && s[start] == '0') return false;
int num = 0;
for (int i = start; i <= end; i++) {
if (s[i] < '0' || s[i] > '9') return false;
num = num * 10 + (s[i] - '0');
if (num > 255) return false;
}
return true;
}
vector result;
void backtracking(string s, int startIndex, int point) {
if (point == 3) {
if (IPstr(s, startIndex, s.size() -1)) result.push_back(s);
return ;
}
for (int i = startIndex; i < s.size(); i++) {
if (IPstr(s, startIndex, i)) {
s.insert(s.begin() + i + 1, '.');
point++;
backtracking(s, i + 2, point);
s.erase(s.begin() + i + 1); // erase(pos)删除pos处的一个字符
point--;
}
else break;
}
}
vector restoreIpAddresses(string s) {
backtracking(s, 0, 0);
return result;
}
};
8.子集(78)
- 组合问题和分割问题都是收集树的叶子节点,而子集问题是找树的所有结点
class Solution {
public:
vector> result;
vector path;
void backtracking(vector& nums, int startIndex) {
result.push_back(path); // 收集所有结点
if (startIndex >= nums.size()) return;
for (int i = startIndex; i < nums.size(); i++) {
path.push_back(nums[i]);
backtracking(nums, i + 1);
path.pop_back();
}
}
vector> subsets(vector& nums) {
backtracking(nums, 0);
return result;
}
};
9.子集II(90)
class Solution {
public:
vector> result;
vector path;
void backtracking(vector& nums, int startIndex, vector used) {
result.push_back(path);
if (startIndex >= nums.size()) return;
for (int i = startIndex; i < nums.size(); i++) {
if (i > 0 && nums[i - 1] == nums[i] && used[i - 1] == false) continue;
path.push_back(nums[i]);
used[i] = true;
backtracking(nums, i + 1, used);
used[i] = false;
path.pop_back();
}
}
vector> subsetsWithDup(vector& nums) {
vector used(nums.size(), false);
sort(nums.begin(), nums.end()); // 注意先排序
backtracking(nums, 0, used);
return result;
}
};
10.递增子序列(491)
不能对vector进行排序即不能用used数组进行剪枝,可以用set
class Solution {
public:
vector> result;
vector path;
void backtracking(vector& nums, int startIndex) {
if (path.size() >= 2) result.push_back(path);
if (startIndex >= nums.size()) return ;
unordered_set uset;
for (int i = startIndex; i < nums.size(); i++) {
if ((!path.empty() && nums[i] < path.back()) || uset.find(nums[i]) != uset.end()) continue;
uset.insert(nums[i]);
path.push_back(nums[i]);
backtracking(nums, i + 1);
path.pop_back();
}
}
vector> findSubsequences(vector& nums) {
backtracking(nums, 0);
return result;
}
};
11.全排列(46)
- 排列问题每层都是从0开始搜索而不是startIndex,需要used数组记录path里都放了哪些元素了
- 同一支树去重used[i] == true;同一层去重used[i - 1] == false。且排列问题startIndex = 0
class Solution {
public:
vector> result;
vector path;
void backtracking(vector& nums, vector used) {
if (path.size() == nums.size()) {
result.push_back(path);
return ;
}
for (int i = 0; i < nums.size(); i++) {
if (used[i] == true) continue;
used[i] = true;
path.push_back(nums[i]);
backtracking(nums, used);
path.pop_back();
used[i] = false;
}
}
vector> permute(vector& nums) {
vector used(nums.size(), false);
backtracking(nums, used);
return result;
}
};
12.全排列II(47)
同一层和同一支树都要去重
class Solution {
public:
vector> result;
vector path;
void backtracking(vector& nums, vector used) {
if (path.size() == nums.size()) {
result.push_back(path);
return ;
}
for (int i = 0; i < nums.size(); i++) {
if ((i > 0 && used[i - 1] == false && nums[i - 1] == nums[i]) || used[i] == true) continue;
used[i] = true;
path.push_back(nums[i]);
backtracking(nums, used);
path.pop_back();
used[i] = false;
}
}
vector> permuteUnique(vector& nums) {
sort(nums.begin(), nums.end());
vector used(nums.size(), false);
backtracking(nums, used);
return result;
}
};
13.重新安排行程(332)
class Solution {
public:
// unordered_map<出发机场, map<到达机场, 航班次数>>
unordered_map> umap;
vector res;
bool backtracking(int ticketNum, vector& res) {
if (res.size() == ticketNum + 1) return true;
for (auto& p : umap[res[res.size() - 1]]) { // 注意p时引用传递
if (p.second > 0) {
p.second--;
res.push_back(p.first);
if (backtracking(ticketNum, res)) return true;
p.second++;
res.pop_back();
}
}
return false;
}
vector findItinerary(vector>& tickets) {
for (auto t : tickets) umap[t[0]][t[1]]++; // 注意格式
res.push_back("JFK");
backtracking(tickets.size(), res);
return res;
}
};
14.N皇后(51)
class Solution {
public:
vector> res;
bool isvalid(int row, int col, vector board, int n) {
for (int i = 0; i < row; i++) if (board[i][col] == 'Q') return false;
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) if (board[i][j] == 'Q') return false;
for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) if (board[i][j] == 'Q') return false;
return true;
}
void backtracking(int row, vector& board, int n) {
if (row == n) {
res.push_back(board);
return ;
}
for (int col = 0; col < n; col++) {
if (isvalid(row, col, board, n)) {
board[row][col] = 'Q';
backtracking(row + 1, board, n);
board[row][col] = '.';
}
}
}
vector> solveNQueens(int n) {
vector board(n, string(n, '.'));
backtracking(0, board, n);
return res;
}
};
15.解数独(37)
class Solution {
public:
bool isvalid(int row, int col, char c, vector> board) {
for (int i = 0; i < 9; i++) if (board[i][col] == c) return false;
for (int j = 0; j < 9; j++) if (board[row][j] == c) return false;
int startX = row / 3 * 3;
int startY = col / 3 * 3;
for (int i = startX; i < startX + 3; i++) {
for (int j = startY; j < startY + 3; j++) {
if (board[i][j] == c) return false;
}
}
return true;
}
bool backtracing(vector>& board) {
for (int i = 0; i < board.size(); i++) {
for (int j = 0; j < board[0].size(); j++) {
if (board[i][j] != '.') continue;
for (char k = '1'; k <= '9'; k++) {
if (isvalid(i, j, k, board)) {
board[i][j] = k;
if (backtracing(board)) return true;
board[i][j] = '.';
}
}
return false; // 递归终止
}
}
return true;
}
void solveSudoku(vector>& board) {
backtracing(board);
}
};
八、贪心
贪心没有固定套路,从局部最优推整体最优
1.分发饼干(455)
// 小饼干满足小胃口
class Solution {
public:
int findContentChildren(vector& g, vector& s) {
sort(g.begin(), g.end());
sort(s.begin(), s.end());
int i = 0, j = 0, res = 0;
for (; j < s.size(); j++) { // 先遍历饼干
if (i < g.size() && s[j] >= g[i]) {
i++; // 再遍历孩子
res++;
}
}
return res;
}
};
2.摆动序列(376)
class Solution {
public:
// 情况一:上下坡中有平坡
// 情况二:数组首尾两端
// 情况三:单调坡中有平坡
int wiggleMaxLength(vector& nums) {
int preDiff = 0;
int curDiff = 0;
int res = 1; // 情况二
for (int i = 0; i < nums.size() - 1; i++) {
curDiff = nums[i + 1] - nums[i];
// 情况一:等于号
if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {
res++;
preDiff = curDiff; // 情况三,只有在波动时更新preDiff
}
}
return res;
}
};
3.最大子数组和(53)
class Solution {
public:
int maxSubArray(vector& nums) {
int res = INT_MIN;
int count = 0;
for (int i = 0; i < nums.size(); i++) {
count += nums[i];
if (count > res) res = count;
if (count < 0) count = 0;
}
return res;
}
};
4.买卖股票的最佳时期 II(122)
class Solution {
public:
int maxProfit(vector& prices) {
int res = 0;
for (int i = 0; i < prices.size() - 1; i++) {
// 只收集正利润
if (prices[i + 1] - prices[i] > 0) res += prices[i + 1] - prices[i];
}
return res;
}
};
5.跳跃游戏(55)
class Solution {
public:
bool canJump(vector& nums) {
int cover = 0;
for (int i = 0; i <= cover; i++) { // 注意i是小于等于cover的
if (i + nums[i] > cover) cover = i + nums[i];
if (cover >= nums.size() - 1) return true;
}
return false;
}
};
6.跳跃游戏II(45)
class Solution {
public:
int jump(vector& nums) {
int curDistance = 0;
int nextDistance = 0;
int res = 0;
for (int i = 0; i < nums.size() - 1; i++) { // 控制移动下标i只移动到nums.size() - 2的位置
nextDistance = max(i + nums[i], nextDistance);
if (i == curDistance) {
res++;
curDistance = nextDistance;
}
}
return res;
}
};
7.K次取反后最大化的数组和(1005)
class Solution {
public:
int largestSumAfterKNegations(vector& nums, int k) {
sort(nums.begin(), nums.end());
for (int i = 0; i < nums.size() && k > 0; i++) {
if (nums[i] < 0) {
nums[i] = -nums[i];
k--;
}
}
sort(nums.begin(), nums.end()); // 注意重新排序
if (k % 2 == 1) nums[0] = -nums[0];
int res = 0;
for (int i = 0; i < nums.size(); i++) res += nums[i];
return res;
}
};
8.加油站(134)
class Solution {
public:
int canCompleteCircuit(vector& gas, vector& cost) {
int curSum = 0, totalSum = 0, start = 0;
for (int i = 0; i < gas.size(); i++) {
curSum += gas[i] - cost[i];
totalSum += gas[i] - cost[i];
if (curSum < 0) { // 如果[0, i]区间和小于0,则一定不是从[0, i]开始
curSum = 0;
start = i + 1;
}
}
if (totalSum < 0) return -1; // 如果总的加油量大于等于总的耗油量是一定可以走完一圈的,否则一定走不完
return start;
}
};
9.分发糖果(135)
class Solution {
public:
int candy(vector& ratings) {
vector vec(ratings.size(), 1);
// 先确定右边大于左边的情况,是从左往右遍历(从小到大遍历)
for (int i = 1; i < ratings.size(); i++) {
if (ratings[i] > ratings[i - 1]) vec[i] = vec[i - 1] + 1;
}
// 之后确定左边大于右边的情况,是从右往左遍历(从小到大遍历),可以举例说明从左往右遍历是不对的
for (int i = ratings.size() - 2; i >= 0; i--) {
if (ratings[i] > ratings[i + 1]) vec[i] = max(vec[i], vec[i + 1] + 1);
}
int res = 0;
for (int i = 0; i < vec.size(); i++) res += vec[i];
return res;
}
};
10.柠檬水找零(860)
class Solution {
public:
// 实时统计5美元和10美元的数量
bool lemonadeChange(vector& bills) {
int five = 0;
int ten = 0;
for (int i = 0; i < bills.size(); i++) {
if (bills[i] == 5) five++;
if (bills[i] == 10) {
if (five > 0) {
ten++;
five--;
} else return false;
}
if (bills[i] == 20) {
if (five > 0 && ten > 0) { // 先消耗10美元
five--;
ten--;
} else if (five >= 3) five -= 3; // 再消耗5美元
else return false;
}
}
return true;
}
};
11.根据身高重建队列(406)
class Solution {
public:
static bool cmp(const vector& a, const vector& b) {
// sort排序规则和我们平时认知一样,而顶堆相反
if (a[0] == b[0]) return a[1] < b[1];
return a[0] > b[0];
}
vector> reconstructQueue(vector>& people) {
// 当有两个维度时,先确定一个维度再确定另外一个,本题先确定身高高的在前,再确定排序位置
sort(people.begin(), people.end(), cmp);
vector> vec;
for (int i = 0; i < people.size(); i++) {
int pos = people[i][1];
vec.insert(vec.begin() + pos, people[i]); // 注意在新vector插入,而不是people
}
return vec;
}
};
12.用最少数量的箭引爆气球(452)
class Solution {
public:
static bool cmp(const vector&a, const vector& b) {
return a[0] < b[0];
}
int findMinArrowShots(vector>& points) {
// 按气球的头从小到大排序
sort(points.begin(), points.end(), cmp);
int res = 1; // 最少需要一支箭
// 从前到后遍历
for (int i = 1; i < points.size(); i++) {
if (points[i][0] > points[i - 1][1]) res++; // 如果两个气球不相邻,则需要增加一支箭
else points[i][1] = min(points[i][1], points[i - 1][1]); // 最小右边界
}
return res;
}
};
13.无重叠区间(435)
class Solution {
public:
static bool cmp(const vector& a, const vector& b) {
return a[0] < b[0];
}
int eraseOverlapIntervals(vector>& intervals) {
sort(intervals.begin(), intervals.end(), cmp);
int res = 0; // 记录重叠区间的个数
int end = intervals[0][1];
for (int i = 1; i < intervals.size(); i++) {
if (intervals[i][0] >= end) end = intervals[i][1]; // 区间不重叠
else { // 区间重叠
end = min(end, intervals[i][1]);
res++;
}
}
return res;
}
};
14.划分字母区间(763)
class Solution {
public:
vector partitionLabels(string s) {
// 利用哈希表记录每个字母出现的最远下标
int hash[26] = {0};
vector vec;
for (int i = 0; i < s.size(); i++) hash[s[i] - 'a'] = i;
int left = 0, right = 0;
for (int i = 0; i < s.size(); i++) {
right = max(right, hash[s[i] - 'a']);
if (i == right) {
vec.push_back(right - left + 1);
left = i + 1;
}
}
return vec;
}
};
15.合并区间(56)
class Solution {
public:
static bool cmp(const vector& a, const vector& b) {
return a[0] < b[0];
}
vector> merge(vector>& intervals) {
sort(intervals.begin(), intervals.end(), cmp);
vector> res;
res.push_back(intervals[0]);
for (int i = 1; i < intervals.size(); i++) {
// 如果区间重叠
if (res.back()[1] >= intervals[i][0]) res.back()[1] = max(res.back()[1], intervals[i][1]);
// 如果区间不重叠
else res.push_back(intervals[i]);
}
return res;
}
};
16.单调递增的数字(738)
class Solution {
public:
// 当当前位数字大于后一位数字时,当前位数字值减一,后一位数字值变为9
// 倒序遍历
int monotoneIncreasingDigits(int n) {
string strNum = to_string(n);
int flag = strNum.size(); // 变为9的标志位(注意初始值为大于strNum的最大下标值)
for (int i = strNum.size() - 1; i >= 1; i--) {
if (strNum[i - 1] > strNum[i]) {
flag = i;
strNum[i - 1]--;
}
}
for (int i = flag; i < strNum.size(); i++) strNum[i] = '9';
return stoi(strNum);
}
};
17.监控二叉树(968)
/*
0:该节点无覆盖
1:本节点有摄像头
2:本节点有覆盖
*/
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int res = 0;
int traversal(TreeNode* root) {
if (root == NULL) return 2;
int left = traversal(root->left);
int right = traversal(root->right);
// 如果左右两个孩子都有覆盖,则父节点为无覆盖
if (left == 2 && right == 2) return 0;
// 如果左右两个孩子至少一个无覆盖,则父节点需安装摄像头
if (left == 0 || right == 0) {
res++;
return 1;
}
// 如果左右两个孩子至少一个有摄像头,则父节点为有覆盖
if (left == 1 || right == 1) return 2;
return -1;
}
int minCameraCover(TreeNode* root) {
if (traversal(root) == 0) res++;
return res;
}
};
九、动态规划
步骤:
1.确定dp数组的下标及其含义
2.确定递推公式(即状态转移公式)
3.dp数组初始化
4.确定遍历顺序
5.举例推导
1.斐波那契数(509)
class Solution {
public:
int fib(int n) {
if (n <= 1) return n;
vector dp(n + 1, 0); // 注意vector的大小为n+1
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i < n + 1; i++) dp[i] = dp[i - 1] + dp[i - 2];
return dp[n];
}
};
2.爬楼梯(70)
class Solution {
public:
int climbStairs(int n) {
if (n <= 1) return n;
vector dp(n + 1, 0);
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i < n + 1; i++) dp[i] = dp[i - 1] + dp[i - 2];
return dp[n];
}
};
// 完全背包
/*
class Solution {
public:
int climbStairs(int n) {
vector dp(n + 1, 0);
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= 2; j++) {
if (i >= j) dp[i] += dp[i - j];
}
}
return dp[n];
}
};
*/
3.使用最小花费爬楼梯(746)
class Solution {
public:
int minCostClimbingStairs(vector& cost) {
if (cost.size() == 2) return min(cost[0], cost[1]);
vector dp(cost.size() + 1, 0);
dp[0] = 0;
dp[1] = 0;
for (int i = 2; i < cost.size() + 1; i++) dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
return dp[cost.size()];
}
};
4.不同路径(62)
class Solution {
public:
int uniquePaths(int m, int n) {
vector dp(n, 0);
for (int i = 0; i < n; i++) dp[i] = 1;
for (int j = 1; j < m; j++) { // 注意j也是从1开始
for (int i = 1; i < n; i++) {
dp[i] += dp[i - 1];
}
}
return dp[n - 1];
}
};
5.不同路径II(63)
class Solution {
public:
int uniquePathsWithObstacles(vector>& obstacleGrid) {
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
if (obstacleGrid[0][0] == 1 || obstacleGrid[m - 1][n - 1] == 1) return 0;
vector> dp(m, vector(n, 0));
// 初始化注意障碍物后面都不能达到仍为0
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (obstacleGrid[i][j] == 1) continue;
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
};
6.整数拆分(343)
class Solution {
public:
int integerBreak(int n) {
vector dp(n + 1, 0);
dp[2] = 1;
for (int i = 3; i <= n; i++) {
for (int j = 1; j <= i / 2; j++) { // 拆分一个数n使之乘积最大,那么一定是拆分成m个近似相同的子数相乘才是最大的,所以j <= i / 2
dp[i] = max(dp[i], max(j * (i - j), j * dp[i - j])); // dp[i]可以从j * (i - j)和j * dp[i - j]
}
}
return dp[n];
}
};
7.不同的二叉搜索树(96)
class Solution {
public:
int numTrees(int n) {
vector dp(n + 1, 0);
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
dp[i] += dp[j - 1] * dp[i - j];
}
}
return dp[n];
}
};
8.分割等和子集(416)
class Solution {
public:
bool canPartition(vector& nums) {
int sum = 0;
for (int i = 0; i < nums.size(); i++) sum += nums[i];
if (sum % 2 == 1) return false;
int target = sum / 2;
vector dp(10001, 0);
for (int i = 0; i < nums.size(); i++) {
for (int j = target; j >= nums[i]; j--) {
dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
}
}
if (dp[target] == target) return true;
return false;
}
};
9.最后一块石头的重量 II(1049)
class Solution {
public:
int lastStoneWeightII(vector& stones) {
int sum = 0;
for (int i = 0; i < stones.size(); i++) sum += stones[i];
int target = sum / 2;
vector dp(1501, 0);
for (int i = 0; i < stones.size(); i++) {
for (int j = target; j >= stones[i]; j--) {
dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
return sum - dp[target] - dp[target];
}
};
10.目标和(494)
class Solution {
public:
int findTargetSumWays(vector& nums, int target) {
int sum = 0;
for (int i = 0; i < nums.size(); i++) sum += nums[i];
if ((sum + target) % 2 == 1) return 0;
if (abs(target) > sum) return 0;
int bagSize = (sum + target) / 2;
if (bagSize < 0) return 0;
vector dp(bagSize + 1, 0);
dp[0] = 1;
for (int i = 0; i < nums.size(); i++) {
for (int j = bagSize; j >= nums[i]; j--) {
dp[j] += dp[j - nums[i]];
}
}
return dp[bagSize];
}
};
11.一和零(474)
class Solution {
public:
int findMaxForm(vector& strs, int m, int n) {
vector> dp(m + 1, vector(n + 1, 0));
for (string str : strs) {
int zeroNum = 0, oneNum = 0;
for (char c : str) {
if (c == '0') zeroNum++;
else oneNum++;
}
for (int i = m; i >= zeroNum; i--) {
for (int j = n; j >= oneNum; j--) {
dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
}
}
}
return dp[m][n];
}
};
01背包中二维dp数组的两个for遍历的先后循序是可以颠倒;
01背包中一维dp数组的两个for循环先后循序一定是先遍历物品,再遍历背包容量,且内嵌的循环是从大到小遍历,为了保证每个物品仅被添加一次
完全背包中一维dp数组,其实两个for循环嵌套顺序是可以颠倒的,而完全背包的物品是可以添加多次的,所以内循环要从小到大去遍历
总之,01背包用一维dp先从小到大遍历物品,再从大到小遍历背包;完全背包用一维dp可以先从小到大遍历物品,再从小到大遍历背包,也可以先从小到大遍历背包,再从小到大遍历物品,取决于具体题目,如果求组合数就是外层遍历物品内层遍历背包,求排列数就是外层遍历背包内层遍历物品
12.零钱兑换 II(58)
class Solution {
public:
int change(int amount, vector& coins) {
vector dp(amount + 1, 0);
dp[0] = 1;
for (int i = 0; i < coins.size(); i++) {
for (int j = coins[i]; j <= amount; j++) {
dp[j] += dp[j - coins[i]];
}
}
return dp[amount];
}
};
13.组合总和 IV(377)
class Solution {
public:
int combinationSum4(vector& nums, int target) {
vector dp(target + 1, 0);
dp[0] = 1;
for (int j = 0; j <= target; j++) {
for (int i = 0; i < nums.size(); i++) {
if (j - nums[i] >= 0 && dp[j] < INT_MAX - dp[j - nums[i]]) dp[j] += dp[j - nums[i]];
}
}
return dp[target];
}
};
14.完全平方数(279)
class Solution {
public:
int numSquares(int n) {
vector dp(n + 1, INT_MAX);
dp[0] = 0;
for (int i = 1; i * i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (j >= i * i) {
dp[j] = min(dp[j], dp[j - i * i] + 1);
}
}
}
return dp[n];
}
};
15.单词拆分(139)
class Solution {
public:
bool wordBreak(string s, vector& wordDict) {
unordered_set uset(wordDict.begin(), wordDict.end());
vector dp(s.size() + 1, false);
dp[0] = true;
for (int i = 1; i <= s.size(); i++) {
for (int j = 0; j <= i; j++) {
string subStr = s.substr(j, i - j);
if (uset.find(subStr) != uset.end() && dp[j]) {
dp[i] = true;
}
}
}
return dp[s.size()];
}
};
16.打家劫舍(198)
class Solution {
public:
int rob(vector& nums) {
if (nums.size() == 1) return nums[0];
if (nums.size() == 2) return max(nums[0], nums[1]);
vector dp(nums.size());
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);
for (int i = 2; i < nums.size(); i++) {
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
}
return dp[nums.size() - 1];
}
};
17.打家劫舍 II(213)
class Solution {
public:
int rob(vector& nums) {
if (nums.size() == 1) return nums[0];
if (nums.size() == 2) return max(nums[1], nums[0]);
int ret1 = robAction(nums, 0, nums.size() - 2);
int ret2 = robAction(nums, 1, nums.size() - 1);
return max(ret1, ret2);
}
int robAction(vector& nums, int start, int end) {
if (start == end) return nums[start];
vector dp(nums.size());
dp[start] = nums[start];
dp[start + 1] = max(nums[start], nums[start + 1]);
for (int i = 2; i <= end; i++) {
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
}
return dp[end];
}
};
18.打家劫舍 III(337)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector robTree(TreeNode* cur) {
if (cur == NULL) return vector{0, 0};
vector left = robTree(cur->left);
vector right = robTree(cur->right);
int val1 = cur->val + left[0] + right[0];
int val2 = max(left[0], left[1]) + max(right[0], right[1]);
return vector{val2, val1};
}
int rob(TreeNode* root) {
vector res = robTree(root);
return max(res[0], res[1]);
}
};
19.买卖股票的最佳时机(121)
class Solution {
public:
int maxProfit(vector& prices) {
int len = prices.size();
if (len == 0) return 0;
vector> dp(len, vector(2, 0));
dp[0][0] = -prices[0];
dp[0][1] = 0;
for (int i = 1; i < len; i++) {
dp[i][0] = max(dp[i - 1][0], -prices[i]);
dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);
}
return dp[len - 1][1];
}
};
20.买卖股票的最佳时机 II(122)
class Solution {
public:
int maxProfit(vector& prices) {
int len = prices.size();
if (len == 1) return 0;
vector> dp(len, vector(2, 0));
dp[0][0] = -prices[0];
dp[0][1] = 0;
for (int i = 1; i < len; i++) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
}
return dp[len - 1][1];
}
};
21.买卖股票的最佳时机 III(123)
class Solution {
public:
int maxProfit(vector& prices) {
if (prices.size() == 1) return 0;
vector> dp(prices.size(), vector(5, 0));
dp[0][1] = -prices[0];
dp[0][3] = -prices[0];
for (int i = 1; i < prices.size(); i++) {
dp[i][0] = dp[i - 1][0];
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
}
return dp[prices.size() - 1][4];
}
};
22.买卖股票的最佳时机 IV(188)
class Solution {
public:
int maxProfit(int k, vector& prices) {
if (prices.size() == 1) return 0;
vector> dp(prices.size(), vector(2 * k + 1, 0));
for (int j = 1; j < 2 * k + 1; j += 2) dp[0][j] = -prices[0];
for (int i = 1; i < prices.size(); i++) {
for (int j = 0; j < 2 * k - 1; j += 2) {
dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
}
}
return dp[prices.size() - 1][2 * k];
}
};
23.最佳买卖股票时机含冷冻期(309)
class Solution {
public:
int maxProfit(vector& prices) {
if (prices.size() == 0) return 0;
vector> dp(prices.size(), vector(4, 0));
dp[0][0] = -prices[0];
for (int i = 1; i < prices.size(); i++) {
dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][1], dp[i - 1][3]) - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];
}
return max(dp[prices.size() - 1][1], max(dp[prices.size() - 1][2], dp[prices.size() - 1][3]));
}
};
24.买卖股票的最佳时机含手续费(714)
class Solution {
public:
int maxProfit(vector& prices, int fee) {
if (prices.size() == 1) return 0;
vector> dp(prices.size(), vector(2, 0));
dp[0][0] = -prices[0];
dp[0][1] = 0;
for (int i = 1; i < prices.size(); i++) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);
}
return dp[prices.size() - 1][1];
}
};
25.最长递增子序列(300)
class Solution {
public:
int lengthOfLIS(vector& nums) {
if (nums.size() == 1) return 1;
vector dp(nums.size(), 1);
int result = 1;
for (int i = 1; i < nums.size(); i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
}
if (dp[i] > result) result = dp[i];
}
return result;
}
};
26.最长连续递增序列(674)
class Solution {
public:
int findLengthOfLCIS(vector& nums) {
if (nums.size() == 1) return 1;
vector dp(nums.size(), 1);
int result = 1;
for (int i = 0; i < nums.size() - 1; i++) {
if (nums[i + 1] > nums[i]) dp[i + 1] = dp[i] + 1;
if (dp[i + 1] > result) result = dp[i + 1];
}
return result;
}
};
27.最长重复子序列(718)
class Solution {
public:
int findLength(vector& nums1, vector& nums2) {
vector> dp(nums1.size() + 1, vector(nums2.size() + 1, 0));
int result = 0;
for (int i = 1; i <= nums1.size(); i++) {
for (int j = 1; j <= nums2.size(); j++) {
if (nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
if (dp[i][j] > result) result = dp[i][j];
}
}
return result;
}
};
28.最长公共子序列(1143)
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
vector> dp(text1.size() + 1, vector(text2.size() + 1, 0));
for (int i = 1; i <= text1.size(); i++) {
for (int j = 1; j <= text2.size(); j++) {
if (text1[i - 1] == text2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
return dp[text1.size()][text2.size()];
}
};
29.不相交的线(1035)
class Solution {
public:
int maxUncrossedLines(vector& nums1, vector& nums2) {
vector> dp(nums1.size() + 1, vector(nums2.size() + 1, 0));
for (int i = 1; i <= nums1.size(); i++) {
for (int j = 1; j <= nums2.size(); j++) {
if (nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
return dp[nums1.size()][nums2.size()];
}
};
30.最大子数组和(53)
class Solution {
public:
int maxSubArray(vector& nums) {
vector dp(nums.size(), 0);
dp[0] = nums[0];
int result = dp[0];
for (int i = 1; i < nums.size(); i++) {
dp[i] = max(nums[i], dp[i - 1] + nums[i]);
if (dp[i] > result) result = dp[i];
}
return result;
}
};
31.判断子序列(392)
class Solution {
public:
bool isSubsequence(string s, string t) {
vector> dp(s.size() + 1, vector(t.size() + 1, 0));
for (int i = 1; i <= s.size(); i++) {
for (int j = 1; j <= t.size(); j++) {
if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
if (dp[s.size()][t.size()] == s.size()) return true;
else return false;
}
};
32.不同的子序列(115)
class Solution {
public:
int numDistinct(string s, string t) {
vector> dp(s.size() + 1, vector(t.size() + 1, 0));
for (int i = 0; i <= s.size(); i++) dp[i][0] = 1;
for (int i = 1; i <= s.size(); i++) {
for (int j = 1; j <= t.size(); j++) {
if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
else dp[i][j] = dp[i - 1][j];
}
}
return dp[s.size()][t.size()];
}
};
33.两个字符串的删除操作(583)
class Solution {
public:
int minDistance(string word1, string word2) {
vector> dp(word1.size() + 1, vector(word2.size() + 1, 0));
for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
for (int i = 1; i <= word1.size(); i++) {
for (int j = 1; j <= word2.size(); j++) {
if (word1[i - 1] == word2[j - 1]) dp[i][j] = dp[i - 1][j - 1];
else dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + 1;
}
}
return dp[word1.size()][word2.size()];
}
};
34.编辑距离(72)
class Solution {
public:
int minDistance(string word1, string word2) {
vector> dp(word1.size() + 1, vector(word2.size() + 1, 0));
for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
for (int i = 1; i <= word1.size(); i++) {
for (int j = 1; j <= word2.size(); j++) {
if (word1[i - 1] == word2[j - 1]) dp[i][j] = dp[i - 1][j - 1];
else dp[i][j] = min(dp[i - 1][j], min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;
}
}
return dp[word1.size()][word2.size()];
}
};
35.回文子串(647)
class Solution {
public:
int countSubstrings(string s) {
vector> dp(s.size(), vector(s.size(), false));
int result = 0;
for (int i = s.size() - 1; i >= 0; i--) {
for (int j = i; j < s.size(); j++) {
if (s[i] == s[j]) {
if (j - i <= 1) {
result++;
dp[i][j] = true;
} else if (dp[i + 1][j - 1]) {
result++;
dp[i][j] = true;
}
}
}
}
return result;
}
};
36.最长回文子串(516)
class Solution {
public:
int longestPalindromeSubseq(string s) {
vector> dp(s.size(), vector(s.size(), 0));
for (int i = 0; i < s.size(); i++) dp[i][i] = 1;
for (int i = s.size() - 1; i >= 0; i--) {
for (int j = i + 1; j < s.size(); j++) {
if (s[i] == s[j]) dp[i][j] = dp[i + 1][j - 1] + 2;
else dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
}
}
return dp[0][s.size() - 1];
}
};
十、单调栈
1.每日温度(739)
class Solution {
public:
vector dailyTemperatures(vector& temperatures) {
stack st;
vector result(temperatures.size(), 0);
st.push(0);
for (int i = 1; i < temperatures.size(); i++) {
if (temperatures[i] <= temperatures[st.top()]) st.push(i);
else {
while (!st.empty() && temperatures[i] > temperatures[st.top()]) {
result[st.top()] = i - st.top();
st.pop();
}
st.push(i);
}
}
return result;
}
};
2.下一个更大元素 I(496)
class Solution {
public:
vector nextGreaterElement(vector& nums1, vector& nums2) {
vector result(nums1.size(), -1);
unordered_map umap;
for (int i = 0; i < nums1.size(); i++) {
umap[nums1[i]] = i;
}
stack st;
st.push(0);
for (int i = 1; i < nums2.size(); i++) {
if (nums2[st.top()] >= nums2[i]) st.push(i);
else {
while (!st.empty() && nums2[st.top()] < nums2[i]) {
if (umap.find(nums2[st.top()]) != umap.end()) {
int idx = umap[nums2[st.top()]];
result[idx] = nums2[i];
}
st.pop();
}
st.push(i);
}
}
return result;
}
};
3.下一个更大元素 II(503)
class Solution {
public:
vector nextGreaterElements(vector& nums) {
vector nums0(nums.begin(), nums.end());
nums.insert(nums.end(), nums0.begin(), nums0.end());
vector result(nums.size(), -1);
stack st;
st.push(0);
for (int i = 1; i < nums.size(); i++) {
while (!st.empty() && nums[st.top()] < nums[i]) {
result[st.top()] = nums[i];
st.pop();
}
st.push(i);
}
result.resize(nums.size() / 2);
return result;
}
};
4.接雨水(42)
class Solution {
public:
int trap(vector& height) {
if (height.size() <= 2) return 0;
int sum = 0;
stack st;
st.push(0);
for (int i = 1; i < height.size(); i++) {
if (height[i] < height[st.top()]) {
st.push(i);
} else if (height[i] == height[st.top()]) {
st.pop();
st.push(i);
} else {
while (!st.empty() && height[i] > height[st.top()]) {
int mid = height[st.top()];
st.pop();
if (!st.empty()) {
int h = min(height[st.top()], height[i]) - mid;
int w = i - st.top() - 1;
sum += h * w;
}
}
st.push(i);
}
}
return sum;
}
};
5.柱状图中最大的矩形(84)
class Solution {
public:
int largestRectangleArea(vector& heights) {
heights.insert(heights.begin(), 0);
heights.push_back(0);
stack st;
st.push(0);
int result = 0;
for (int i = 1; i < heights.size(); i++) {
if (heights[i] > heights[st.top()]) {
st.push(i);
} else if (heights[i] == heights[st.top()]) {
st.pop();
st.push(i);
} else {
while (!st.empty() && heights[i] < heights[st.top()]) {
int mid = heights[st.top()];
st.pop();
if (!st.empty()) {
int h = mid;
int w = i - st.top() - 1;
result = max(result, h * w);
}
}
st.push(i);
}
}
return result;
}
};