数字IC经典电路(2)——经典乘法器的实现(乘法器简介及Verilog实现)
乘法器简介及Verilog实现
- 写在前面的话
-
- 乘法器分类
- 经典乘法器
-
- 8bit并行乘法器
- 8bit移位相加乘法器
- 优化后的8bit移位相加乘法器
- 查找表乘法器
- 加法树乘法器
- booth乘法器
- wallace树乘法器
- carry-save乘法器
- 阵列乘法器
- 总结
写在前面的话
数字电路中乘法器是一种常见的电子元件,其基本含义是将两个数字相乘,并输出其乘积。与加法器不同,乘法器可以实现更复杂的运算,因此在数字电路系统中有着广泛的应用。
乘法器的主要用途是在数字信号处理、计算机科学以及其他数字电路应用中进行精确的数字乘法运算。例如,在数字信号处理中,乘法器通常用于数字滤波器中的系数乘法;在计算机科学中,它们被用于执行浮点运算;而在其他数字电路应用中,乘法器也可以实现时域和频域的变换等。
在数字电路系统中,乘法器的重要性无法被忽视。它们不仅能够提高数字信号处理和计算机科学中的运算速度和精度,还能够实现更复杂的数字信号处理和分析。此外,乘法器还可以优化数字信号处理的功耗和面积,从而使得数字电路系统具有更优异的性能。
数字电路乘法器在现代电子技术中扮演着重要的角色。它们为数字信号处理、计算机科学以及其他数字电路应用提供了精确的数字乘法运算,并且可以进一步优化数字电路系统的性能,使其具有更高的效率和可靠性。随着人们对数字信号处理和计算机科学的需求不断增加,乘法器将继续发挥着重要的作用,为数字电路应用提供更好的解决方案。
乘法器分类
在数字集成电路中,乘法器的种类主要可以分为以下三类:
- 串行乘法器:这种乘法器是最简单的乘法器之一,它将两个数的乘积通过一个计数器逐位相加得到。由于每一位的运算都需要消耗时间,因此串行乘法器的速度较慢。
- 并行乘法器:与串行乘法器不同,这种乘法器可以同时对多位进行运算,因此运算速度更快。常见的并行乘法器有布斯-加勒德算法和沃勒斯算法等。
- 快速乘法器:这种乘法器采用了更高级的算法,在乘法过程中将输入的数按位划分,并尝试最小化运算次数。常见的快速乘法器包括批处理器算法、底数为2的Booth算法、Wallace树算法和Dadda树算法等。这些算法都比串行和并行乘法器更快且节省空间。
在数字集成电路中,乘法器的种类繁多,每种乘法器都有其适用的场合。选择适合自己需求的乘法器可以有效地提高系统的性能和效率。
经典乘法器
8bit并行乘法器
并行乘法器是纯组合类型的乘法器,完全由基本逻辑门搭建而成,在Verilog中支持乘法运算操作符,实现基本的乘法只需简单的命令即可。
Verilog代码:
// -----------------------------------------------------------------------------
// Copyright (c) 2014-2023 All rights reserved
// -----------------------------------------------------------------------------
// Author : HFUT90S [email protected]
// File : para_mult.v
// Create : 2023-03-21 11:10:17
// Revise : 2023-03-21 11:10:17
// Editor : 0078
// Verdion: v1.0
// Description: 8bit parallel multiplier
// -----------------------------------------------------------------------------
module para_mult #(parameter N = 8 )(
input [N:1] a , // data in a
input [N:1] b , // data in b
output wire [2*N:1] out // mult out
);
assign out = a*b ;
endmodule
这里借助HDL和EDA综合软件,实现容易,运算速度快,但耗用资源多,尤其是当乘法运算的位数较宽时,其耗用的资源将会非常庞大。
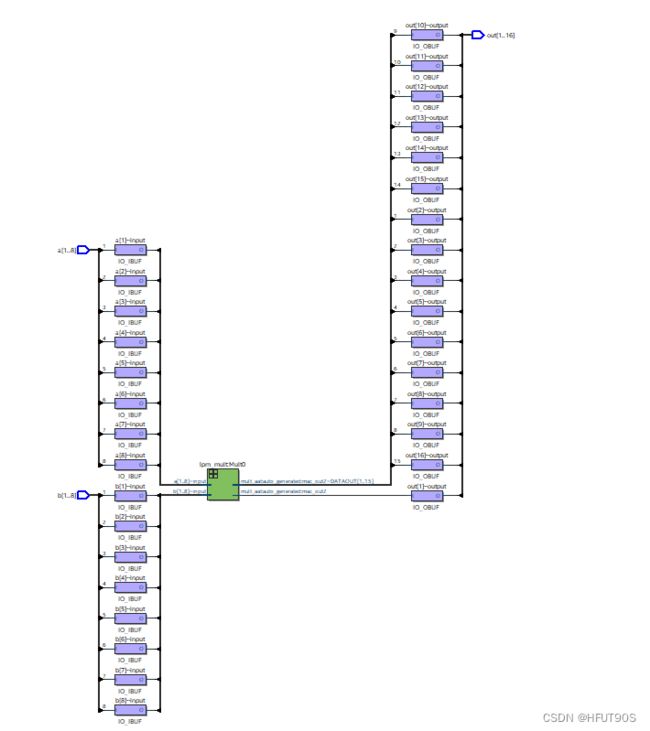
Quartus RTL图
耗用资源较多,看不出使用的具体结构。
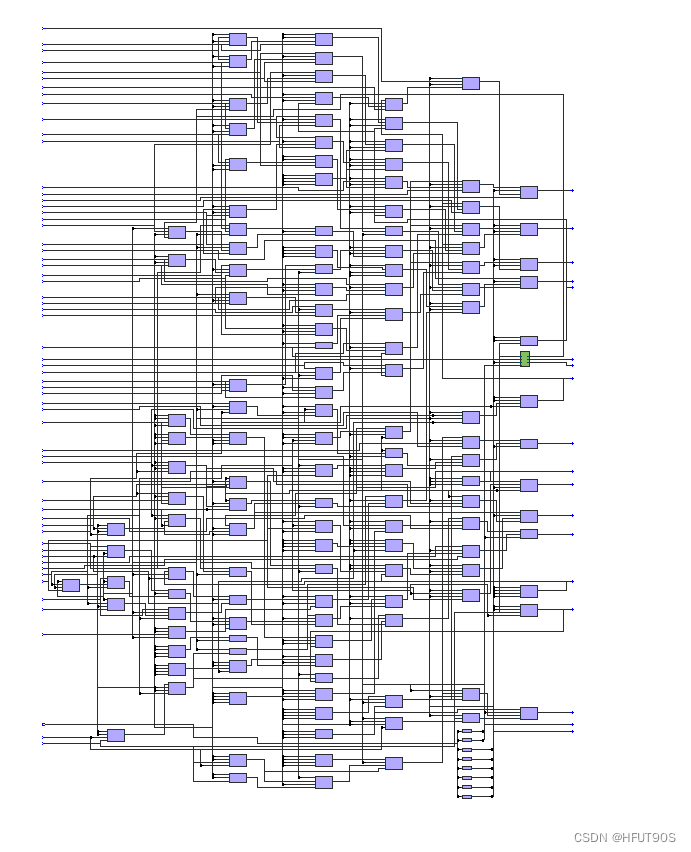
Quartus Post mapping图
8bit移位相加乘法器
移位相加乘法器是最节省资源的乘法器设计方式,设计思路为逐项相加,根据乘数每一位是否为1进行计算,为1则将被乘数移位相加。这种方法硬件资源耗用少,8位乘法器只需要16位移位寄存器和16位加法器即可。
以下是移位相加乘法器的操作步骤:
- 将乘数和被乘数转换为二进制数。
- 将乘数的每个二进制位从低位到高位逐个取出,如果该位为1,则将被乘数左移相应的位数后与部分积相加。
- 重复第2步,直到乘数的所有二进制位都处理完毕,此时得到的部分积即为最终结果。
例如,假设要计算5×6,首先将5和6转换为二进制数101和110,然后从低位到高位依次处理乘数的每个二进制位,得到以下过程:
- 当处理乘数的最低位1时,将被乘数5左移0位后加到部分积中,即得到部分积101。
- 当处理乘数的次低位0时,不需要加入任何东西,部分积保持不变,仍为101。
- 当处理乘数的最高位1时,将被乘数5左移2位后加到部分积中,即得到部分积1111。
因此,最终结果为1111,即十进制下的30。
Verilog代码:
// Verdion: v1.0
// Description: 8bit shift add multiplier
// -----------------------------------------------------------------------------
module shift_add_mult (
input [7:0] operand1 , // 8-bit multiplier A
input [7:0] operand2 , // 8-bit multiplier B
output wire [15:0] result // 16-bit product P
);
reg [7:0] temp;
reg [15:0] adder_result;
integer i ;
always @(*) begin
temp = operand2;
adder_result = 0;
for (i = 0; i < 8; i = i + 1) begin
if (operand1[i] == 1) begin
adder_result = adder_result + (temp << i);
end
end
end
assign result = adder_result;
endmodule
Quartus RTL图
设计中出现多层加法器和移位寄存器。

Quartus Post mapping图
这里使用for循环产生的,可以看出在综合实现时资源占用相对较多;

优化后的8bit移位相加乘法器
上述移位相加乘法器在综合实现时占用资源较多,在FPGA上实现时需要降低资源占用率。修改后的代码如下,加法器的级联结构还具有较好的延迟特性,在时钟频率较高的情况下,仍然能够实现很好的性能。
Verilog代码:
// Verdion: v1.0
// Description:
// -----------------------------------------------------------------------------
module shift_add_mult1(
input [7:0] a, // 8-bit multiplier A
input [7:0] b, // 8-bit multiplier B
output wire [15:0] p // 16-bit product P
);
integer i ;
reg [15:0] product;
reg [15:0] sum;
reg [7:0] shift_reg;
always @(*) begin
product = a * b;
shift_reg = product[7:0]; // 保存乘积的低8位
sum = shift_reg;
for ( i = 0; i < 7; i = i + 1) begin
shift_reg = {shift_reg[6:0], 1'b0}; // 移位并在低位填0
sum = sum + shift_reg; // 级联相加器
end
end
assign p = sum;
endmodule
Quartus RTL图
加法器和移位寄存器数量相对优化前较少。
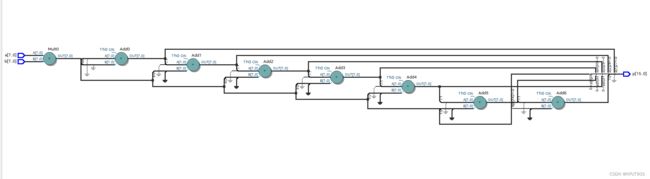
Quartus Post mapping图
相较于优化前的电路结构,资源占用降低超过一半,先前logic element为134,优化后为45。

查找表乘法器
查找表乘法器是将乘积直接存放在存储器中,将操作数(乘数和被乘数)作为地址访问存储器,得到的数据即为乘法结果。查找表乘法器的速度只局限于所使用的存储器的存取速度。由于查找表的规模随着数据位宽呈现指数爆炸,因此不适用于高位宽的乘法操作。
在小型查找表的基础上可以使用加法器共同构成位数较高的乘法器。
Verilog代码:
// -----------------------------------------------------------------------------
// Copyright (c) 2014-2023 All rights reserved
// -----------------------------------------------------------------------------
// Author : HFUT90S [email protected]
// File : lut_mult.v
// Create : 2023-03-21 16:56:58
// Revise : 2023-03-21 16:56:58
// Editor : 0078
// Verdion: v1.0
// Description: 8bit lut multiplier
// -----------------------------------------------------------------------------
module lut_mult(
input [7:0] a , // 8-bit multiplier A
input [7:0] b , // 8-bit multiplier B
output reg [15:0] product // 16-bit product P
);
reg [7:0] look_up_table[0:255];
integer i, j;
always @* begin
// 填充查找表
for (i = 0; i < 256; i = i + 1) begin
look_up_table[i] = i * b;
end
// 使用查找表计算乘积
for (j = 0; j < 8; j = j + 1) begin
if (a[j] == 1'b1) begin
product = product + (look_up_table[b << j]);
end
end
end
endmodule
Quartus RTL图
一团麻,使用居多logic element担任存储器,非常不适用于FPGA设计,在数字IC设计时的适用范围也十分有限。
Quartus Post mapping图
-
资源的使用更多,面积换取更高的运行速度。
由于存储和查表时不需要进行实际的乘法操作,因此查找表乘法器具有高速、低能耗的优点。然而,由于存储查找表所需的存储器容量随n增长速度较快,在多位乘法器上实现时需要花费较多的硬件成本。
加法树乘法器
结合移位相加乘法器和查找表乘法器的优点。
加法树乘法器是一种并行的硬件电路设计,主要用于实现高效的乘法运算。它采用树状结构的加法器来实现多项式乘法,且不需要显式地计算进位或借位。该乘法器的输入是两个被乘数,输出是它们的乘积。
加法树乘法器的实现过程主要分为三步:
-
生成部分积:将两个被乘数分别拆分为若干位二进制数,按照乘法规则计算每一位上的部分积,得到一个二维矩阵。
-
生成加法树:对于每一列的部分积,采用二路并行加法器进行相加,得到一列的加和结果。接着对这些列的加和结果进行二路并行相加,最后得到一个总的加和结果。
-
输出乘积:将最后的加和结果转换为二进制数形式,得到两个被乘数的乘积。
Verilog代码:
// -----------------------------------------------------------------------------
// Copyright (c) 2014-2023 All rights reserved
// -----------------------------------------------------------------------------
// Author : HFUT90S [email protected]
// File : add_tree_mult.v
// Create : 2023-03-21 19:18:21
// Revise : 2023-03-21 19:18:21
// Editor : 0078
// Verdion: v1.0
// Description: 8bit add tree mlutiplier
// -----------------------------------------------------------------------------
module add_tree_mult (
input [7:0] a , // 8-bit multiplier A
input [7:0] b , // 8-bit multiplier B
input clk , // clock
output wire [15:0] out // 16-bit product P
);
//signal define
wire [14:0] out1 ;
wire [14:0] c1 ;
wire [12:0] out2 ;
wire [10:0] out3 ;
wire [10:0] c2 ;
wire [8:0] out4 ;
reg [14:0] temp0 ;
reg [13:0] temp1 ;
reg [12:0] temp2 ;
reg [11:0] temp3 ;
reg [10:0] temp4 ;
reg [9:0] temp5 ;
reg [8:0] temp6 ;
reg [7:0] temp7 ;
function [7:0] mult8X1 ; //实现8X1乘法
input [7:0] operand ;
input sel ;
begin
mult8X1 = (sel)?(operand):8'b0000_0000 ;
end
endfunction
always@(posedge clk ) begin //调用函数实现操作数b各位与操作数a的相乘
temp7 <= mult8X1(a,b[0]) ;
temp6 <= ((mult8X1(a,b[1]))<<1) ;
temp5 <= ((mult8X1(a,b[2]))<<2) ;
temp4 <= ((mult8X1(a,b[3]))<<3) ;
temp3 <= ((mult8X1(a,b[4]))<<4) ;
temp2 <= ((mult8X1(a,b[5]))<<5) ;
temp1 <= ((mult8X1(a,b[6]))<<6) ;
temp0 <= ((mult8X1(a,b[7]))<<7) ;
end
assign out1 = temp0 + temp1 ; //加法器树运算
assign out2 = temp2 + temp3 ;
assign out3 = temp4 + temp5 ;
assign out4 = temp6 + temp7 ;
assign c1 = out1 + out2 ;
assign c2 = out3 + out4 ;
assign out = c1 + c2 ;
endmodule
Quartus RTL图
结构像是一个树,所以称为加法树乘法器。

booth乘法器
Booth乘法器是一种二进制乘法算法,用于计算两个n位二进制数的乘积。该算法采用了一种类似于除法的方法,可以将乘法的时间复杂度从O(n^2)降低到O(nlogn)。
Booth乘法器通过对第二个乘数进行编码,将每个位上的数值转换为1、0或-1,然后利用乘法和加法运算,对每一位进行计算。具体步骤如下:
-
对第二个乘数进行编码:将每个位与其右侧相邻位比较,如果它们的值相同,就将该位编码为0;否则,将其编码为1或-1。最右侧位的右侧补0。
-
将第一个乘数左移一位,形成一个n+1位的数。同时,将编码后的第二个乘数左移一位。
-
对于从右向左的每个位,进行以下操作:
-
如果该位和前一位相同,就不进行任何操作。
-
如果该位是1且前一位是0(或该位是0且前一位是1),则将第一个乘数加上(或减去)第二个乘数。
- 将第一个乘数右移一位,丢弃其中的多余位,从而得到n位的乘积。
Booth乘法器相对于传统的乘法算法具有一定的优势,因为它可以在保持精度的同时减小运算次数。但是,由于它需要对第二个乘数进行编码,因此需要额外的存储空间,并且其实现较为复杂。
Verilog代码:
// -----------------------------------------------------------------------------
// Copyright (c) 2014-2023 All rights reserved
// -----------------------------------------------------------------------------
// Author : HFUT90S [email protected]
// File : booth_mult.v
// Create : 2023-03-21 19:45:54
// Revise : 2023-03-21 19:45:54
// Editor : 0078
// Verdion: v1.0
// Description: 8bit booth multiplier
// -----------------------------------------------------------------------------
module booth_mult(
input signed [7:0] a,
input signed [7:0] b,
output reg signed [15:0] p
);
reg signed [15:0] prod, a_shift;
reg [3:0] control;
integer i ;
always @ (a or b)
begin
prod <= 0;
a_shift <= {a, 3'b0}; //将a左移3位,以适应Booth算法
control[3:0] <= 4'b0100; //初始控制位为0100
for ( i = 0; i < 4; i = i + 1) begin
//查找当前位和前一位以确定操作
case ({control[3], control[2]})
2'b00: prod <= prod + a_shift; //加
2'b01: prod <= prod - a_shift; //减
2'b10: ; //无操作
2'b11: ; //无操作
endcase
//更新控制位
if (control[1:0] == 2'b10) begin
control[3:1] <= control[2:0];
control[0] <= b[i];
end else if (control[1:0] == 2'b01) begin
control[3:1] <= control[2:0];
control[0] <= ~b[i];
end else begin
control[3:1] <= control[2:0];
control[0] <= 1'b0;
end
end
//将结果右移3位,以消除左移的影响
p <= prod >> 3;
end
endmodule
Quartus RTL图
wallace树乘法器
Wallace树乘法器是一种用于高效地进行二进制乘法运算的算法。它使用了一种递归结构,通过将部分积分解成不同的组合来减少运算时间和硬件资源。
Wallace树乘法器的主要思想是将两个n位数字相乘,分解为三个数之和:一个2n位数、一个n位数和一个n/2位数。这些数字可以通过以下方式计算:
- 将两个n位数字A和B拆分为三个数字X、Y和Z,其中X是最高的2n位,Y是中间的n位,Z是最低的n/2位。
- 计算XY和YZ的积,并将它们相加得到P。
- 将P拆分为三个数字Q、R和S,其中Q是最高的2n位,R是中间的n+1位,S是最低的n-1位。
- 通过计算AB = X2^(2n) + Q2^n + R2^(n) + S1 来计算结果。
Wallace树乘法器使用了一种递归结构来实现这种方法。首先,输入被划分为若干组,并在每组内执行并行乘法运算。接下来,在每组之间执行串行运算以生成更高级别的部分积。此过程重复多次直到只剩下一个完整的部分积。
Wallace树乘法器可以在减少延迟和硬件资源消耗方面提供优势。但由于其递归结构需要大量控制逻辑,因此可能会增加设计复杂性。
Verilog代码:
// -----------------------------------------------------------------------------
// Copyright (c) 2014-2023 All rights reserved
// -----------------------------------------------------------------------------
// Author : HFUT90S [email protected]
// File : wallace_mult.v
// Create : 2023-03-21 21:05:26
// Revise : 2023-03-21 21:05:26
// Editor : 0078
// Verdion: v1.0
// Description: wallace_multiplier
// -----------------------------------------------------------------------------
module wallace_mult(A, B, P);
input [7:0] A, B; // 输入 A 和 B 为 8 位数据
output [15:0] P; // 输出 P 为 16 位数据
wire [7:0] C1, C2, C3, C4; // 记录中间结果
wire [7:0] S1, S2, S3; // 记录加法结果
// 直接进行最低位的乘法
assign C1 = A * B[0];
// 计算各个中间结果,用 & 运算表示进位
assign S1 = A * B[2:1];
assign C2 = S1[1] & S1[0];
assign S2 = { S1[5:2], A } * { B[4:3], 2'b0 };
assign C3 = S2[3] & (S2[2] | C2);
assign S3 = { S2[6:4], A } * { B[6:5], 2'b0 };
assign C4 = S3[5] & (S3[4] | C3);
// 计算最高位的进位
wire carry_in = C4 | (S3[4] & S2[2]) | (S2[2] & S1[1]) | (S1[1] & B[0]);
// 计算最终结果
assign P = { carry_in, S3[6:0] };
endmodule
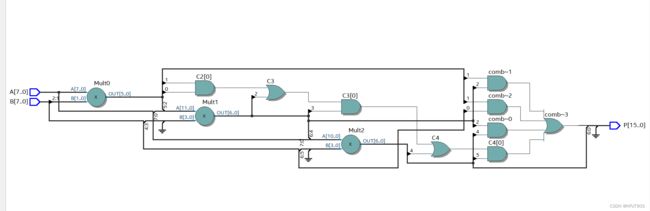
Quartus RTL图
carry-save乘法器
- Carry-save乘法器是一种用于高速乘法的数字电路,它可以在几个时钟周期内完成两个大数的乘法运算。相比传统的乘法器,carry-save乘法器具有更高的并行性和更低的延迟。
- carry-save乘法器使用了一种特殊的编码方式,将两个大数分别表示为三个小数之和(即三进制编码),然后通过对这些小数进行加法运算得到结果。这种编码方式可以充分利用数字电路中加法器的并行性,从而提高计算速度。
- carry-save乘法器包括三个部分:部分积生成器、部分积压缩器和最终结果生成器。在部分积生成器中,输入的两个大数经过三进制编码后被拆分成多个小数,并通过逐位相乘得到所有可能的部分积。然后,在部分积压缩器中,这些部分积经过加法运算被压缩成两组中间结果。最后,在最终结果生成器中,这两组中间结果再次经过加法运算得到最终结果。
- carry-save乘法器通过巧妙地利用三进制编码和并行加法运算实现了高速、低延迟的乘法运算。它在现代数字电路设计中广泛应用于各种计算机系统、通信设备等领域。
Verilog代码:
// -----------------------------------------------------------------------------
// Author : HFUT90S [email protected]
// File : carry_save_mult.v
// Create : 2023-03-22 10:45:27
// Revise : 2023-03-22 10:45:27
// Editor : 0078
// Verdion: v1.0
// Description:
// -----------------------------------------------------------------------------
module carry_save_mult(
input [7:0] a, // 8-bit multiplier A
input [7:0] b, // 8-bit multiplier B
output wire [15:0] p // 16-bit product P
);
wire [7:0] a0, a1, b0, b1;
wire [15:0] p0, p1, p2;
// Split inputs into two 4-bit parts
assign a0 = a[3:0];
assign a1 = a[7:4];
assign b0 = b[3:0];
assign b1 = b[7:4];
// Calculate partial products
assign p0 = a0 * b0;
assign p1 = a0 * b1;
assign p2 = a1 * b0;
// Calculate carry-save product
assign p[7:0] = p0[3:0];
assign p[11:8] = p1[3:0] + p2[3:0];
assign p[15:12] = p2[7:4];
endmodule
Quartus RTL图
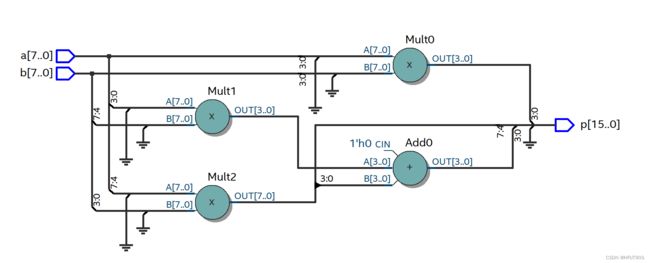
Quartus Post mapping图

阵列乘法器
- 阵列乘法器由多个加法器和乘法器组成,其工作原理是将待乘数和乘数分别按位拆分成多个小段,在阵列乘法器中进行乘法运算和累加,并最终得出乘积。
- 阵列乘法器将待乘数和乘数逐位相乘,并将结果送入加法器进行累加。在每个时钟周期中,阵列乘法器会对每个乘数位进行一次部分积计算,直到所有位都完成运算。部分积计算完成后,阵列乘法器会将结果根据位数进行排序和加和,以得到最终乘积。
- 阵列乘法器的优点是速度快、复杂度低、结构简单等。它广泛应用于数字信号处理、数值计算、图像处理等领域中,是实现大规模数据处理的重要工具。
Verilog代码:
//-------------------------------------------------------------------------
// Copyright (c) 2014-2023 All rights reserved
// -----------------------------------------------------------------------------
// Author : HFUT90S [email protected]
// File : array_mult.v
// Create : 2023-03-22 11:10:13
// Revise : 2023-03-22 11:10:13
// Editor : 0078
// Verdion: v1.0
// Description: array multiplier
// -----------------------------------------------------------------------------
module array_mult(
input [7:0] A, // 输入A
input [7:0] B, // 输入B
output reg [15:0] P // 乘积P
);
wire [7:0] A_array [7:0]; // A阵列
wire [7:0] B_array [7:0]; // B阵列
reg [15:0] P_temp [7:0]; // 临时乘积P_temp
// 将A和B分别分配到对应的阵列位置
assign A_array[0] = A;
assign B_array[0] = B;
genvar i;
generate
// 生成每个阵列的定义和连接
for ( i = 1; i < 8; i=i+1) begin : MULTIPLY
assign A_array[i] = A_array[i-1] << 1; // 左移一位
assign B_array[i] = B_array[i-1] >> 1; // 右移一位
// 计算每个阵列位置上的乘积
always @(*) begin
P_temp[i] = A_array[i] * B_array[i];
end
end
endgenerate
integer j;
// 计算总乘积
always @(*) begin
P = P_temp[0];
for ( j = 1; j < 8; j=j+1) begin
P = P + (P_temp[j] << j);
end
end
endmodule
Quartus RTL图

Quartus Post mapping图

总结
随着计算机科学技术的不断发展,乘法器在数字信号处理、计算机控制等领域中被广泛应用。而不同类型的乘法器,都有各自的优点和适用范围。
-
并行乘法器:
并行乘法器是采用多个乘法器并联运算的方式,通过并行处理提高了乘法器的速度。该乘法器的速度快,适用于高速乘法运算,但其硬件开销较高,面积较大。 -
移位相加乘法器:
移位相加乘法器采用移位和加法操作实现乘法运算,不需要乘法器,硬件实现简单。但是,其速度较慢,适用于数字信号处理等低速乘法运算。 -
查找表乘法器:
查找表乘法器通过预先计算出乘积表,将乘积表存储在查找表中,乘法运算时查表即可。该乘法器的速度较快,适用于低精度的乘法运算。 -
加法树乘法器:
加法树乘法器采用加法器来相加乘积,能够高效地实现数据的并行处理和链式计算。其硬件复杂度和面积都较小,适用于芯片上集成乘法器的应用。 -
Booth乘法器:
Booth乘法器采用编码和位移混合计算的方式,有效减少了乘法器中的运算步骤,进而提高乘法器的速度和精度。适用于高精度运算、数字信号处理等领域。 -
Wallace树乘法器:
Wallace树乘法器是一种高效的乘法器结构,通过对相邻的部分积进行压缩,减少了乘法器中的加法器数量,从而达到减小硬件成本、提高速度的目的。适用于高速计算并且不要求过高的精度场合。 -
Carry-save乘法器:
Carry-save乘法器通过将乘积转化为进位和不进位两部分,分别存储、处理,减少了加法器的数量,提高了乘法器的速度和并行性。适用于高速计算的场合,如图像处理、信号分析等。 -
阵列乘法器:
阵列乘法器是一种多行多列的矩阵结构,采用并行处理的方式实现乘法运算。其硬件成本较低,适用于数字信号处理、图像处理、通信等领域。
在选择乘法器的类型时,需要根据具体的应用场景和需求来选择,以达到最佳的性能和适用范围。