CubeSLAM: Monocular 3D Object SLAM——论文简述
一、简介
提出一种在动态和静态环境中同时进行3D目标检测和定位建图的方法,并且能够互相提升准确度。具体地,对于3D目标,其位置、方向和尺寸通过slam进行了优化;而3D目标作为slam中的路标,可以提供额外的语义和几何约束,从而提升相机位姿估计并减少尺度漂移,且无需回环检测和假设相机的高度不变。
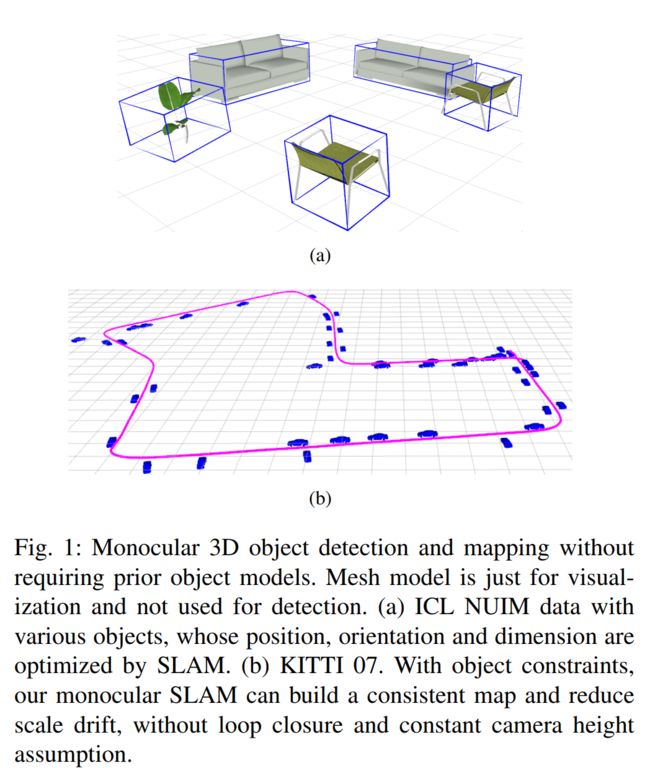
二、Single Image 3D Object Detection
3D box proposal generation
作者利用2D的bbox来生成3D的proposal,而非直接采样。对于一个3D的cuboid,用九个自由度进行表示:R、t以及长宽高(dx,dy,dz),其本身的坐标轴建立在中心位置。而2D的bbox只能提供四条边4个约束,这显然是不够的,因此需要用到物体尺寸和方向等其他信息。
本文没有依赖预测得到的长宽高来减少回归参数,而是采用vanishing point(在两个平行的线条中,两个线条会消失在远方的一点)。对于一个3D的cuboid,可以在xyz轴方向上形成3个VP。
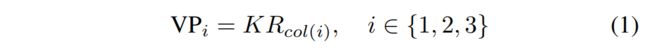
其中K代表相机内参,R代表相对于相机坐标的旋转矩阵,col(i)代表R的第i列。
接下来需要基于得到的VP来获取3D cuboid的8个2D坐标。
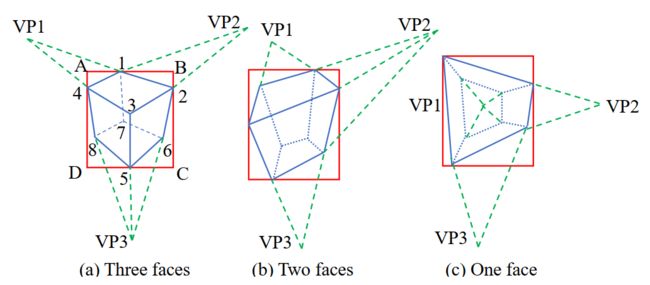
如上所示,我们已经得到了估计的3个VP,仅需估计一个2D点,就可以通过两直线的交点,求出剩余的2D点。
求解3D物体的位姿时,需要区分两种情况:任意姿态物体和地面物体。
对于任意姿态物体,采用 PnP 来求解3D cuboid的位置和尺寸,但由于单目视觉的尺度不确定性,需要确定一个scale。在3D cuboid坐标系下,8个3D点可以表示为[±dx, ±dy, ±dz] / 2,从而3D到2D的投影关系为
![]()
其中π是相机投影函数。这里选择如2、3、4、5这样相邻关系的4个点,每个点提供2个约束,加上提前确定的scale,即可估计3D cuboid的位姿。
对于地面物体,在地平面上建立世界坐标系,那么物体的滚动角和俯仰角均为零,且scale由投影过程中的摄像机高度决定。我们可以直接将下方的2D点反向投影到三维地平面,然后计算其他3D角,形成一个3D cuboid。例如对于图(a)中的p5,用[n,m](相机坐标系下的法向量和距离)表示,其相应的3D点P5是反投影射线 K-1p5 与地平面的交点:
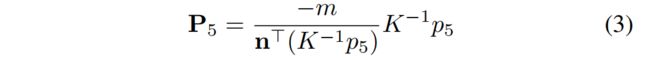
基于上述讨论,求3D物体的proposal转变为求3个VP及1个2D点。VP是由R决定的,可以通过大量的数据训练来直接预测,但本文选择手动采样,然后对它们进行评分排序,以达到普适性的目的。
对于任意姿态物体,需要对整个R进行采样,但对于地面物体,使用相机的滚动角/俯仰角(在数据集SUN RGBD和KITTI中已经提供)和物体的偏航角来计算R。对于视频数据,我们使用slam来估计相机的位姿。因此,采样空间大大缩小。在本文的实验中,只考虑地面物体。
Proposal scoring

代价函数如下:
![]()
其中I代表图像,O代表3D cuboid的9个自由度R、t、d,w1和w2是权重参数,在对小样本数据集进行手动搜索后,设定 w1 = 0.8,w2 = 1.5。本文将损失分为三种:
Distance error:2D cuboid的边缘应与实际图像边缘相匹配。首先进行Canny边缘检测,及距离变换。然后对于每个可见的立方体边缘,对其上的10个点进行均匀采样,并将所有距离值除以2D box的对角线,原理与倒角距离类似。
Angle alignment error:Distance error对物体表面纹理等假阳性边缘非常敏感。因此,我们还用LSD检测长线段(如图 3 中的绿线所示),并测量其角度是否与VP一致。首先根据点-线关系,将这些线段与1个VP相关联。然后,对于每个VP,可以找到斜率最小和最大的两条线段,
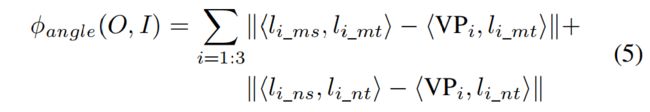
Shape error:前两个代价可以在2D图像空间中有效评估。为了生成更准确的3D proposal,惩罚具有较大长宽比的立方体。我们还可以应用更严格的先验,例如特定类型物体的估计尺寸或固定尺寸。
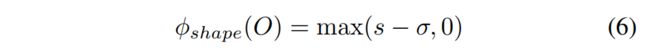
其中s代表最大长宽比,σ在实验中设置为1。
三、OBJECT SLAM
将单图像3D目标检测扩展到多视角object slam,以共同优化物体和相机位姿。该系统使用基于特征点的ORB SLAM2。需要使得BA共同优化目标、路标特征点和相机位姿。
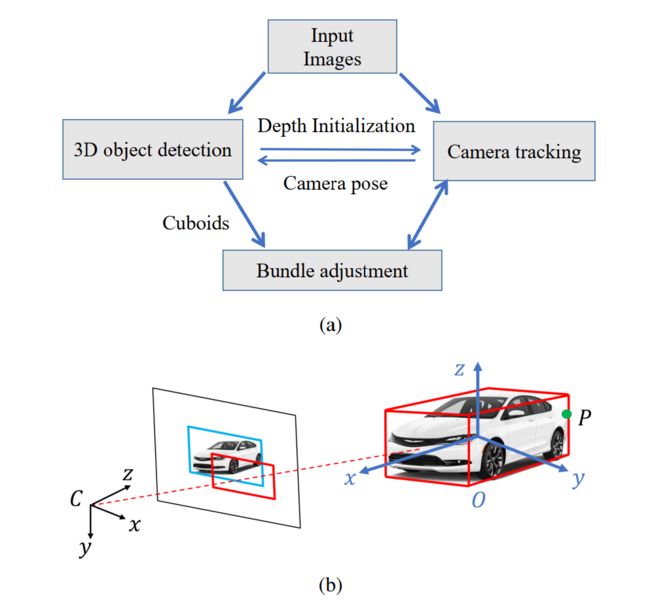
Bundle Adjustment Formulation
BA可以表示为一个非线性最小二乘问题,为了改善鲁棒性,使用 Huber核函数:
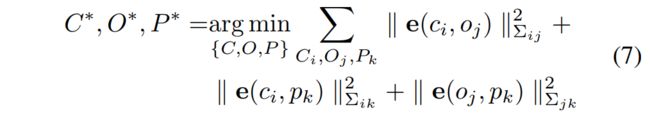
其中C、O、P分别代表相机位姿、3D cuboid和路标点,Σ是不同误差测量值的协方差矩阵。可以使用GN或LM来解决优化问题。GN属于线搜索方法,先找到方向,再确定长度,HΔx=g;LM属于信赖区域方法(Trust Region),认为近似只在区域内可靠,(H+λI)Δx=g,相比于GN,能够保证增量方程的正定性,即认为近似只在一定范围内成立,如果近似不好则缩小范围,从增量方程上来看,可以看成一阶和二阶的混合,参数λ控制着两边的权重。
Measurement Errors
Camera-Object measurement:需要分为3D和2D。
对于3D,在三维物体检测准确的情况下使用。3D物体位姿可以表示为[Tom d]。为了计算3D物体的测量误差,将其转换到相机坐标系:
![]()
om:object measurement, log将SE3的误差映射到6DOF的切向量空间,所以e是9维的。
如果没有物体的先验模型,我们基于图像的cuboid检测就无法区分物体的正面或背面。例如,我们可以通过将物体坐标系旋转90度并交换长度和宽度值来表示相同的长方体。因此,我们需要沿高度方向旋转 0,±90,180,以找到最小误差。
对于2D,将路标投影到图像平面上来获得2D的bbox,然后与检测的bbox比较。简单来说,就是将8个角点投影到平面内,寻找最小和最大的投影像素x,y坐标来建立一个矩形框:
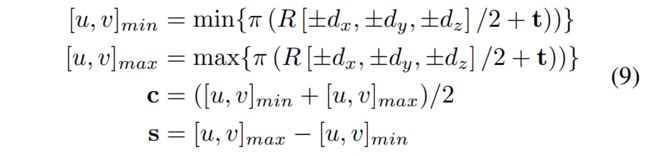
其中c是2D bbox的中心坐标,s是大小。所以可以得到2D下的co误差:
![]()
由于检测过程复杂,与点相比,误差协方差 Σ 或hessian矩阵 W 的建模和估计并不简单。 因此,我们简单地赋予几何接近对象更多的权重。假设cuboid-camera距离为 d,物体的 2D 检测概率为 p,那么我们可以在 KITTI 数据上定义 w = p × max(70 − d,0) / 50,其中 70m 是截断距离。 参数可能因不同的数据集而异。
Object-point measurement:两者之间可以互相提供约束,如果点 P 属于3D物体的对象,则它应该位于 3D cuboid内部。 因此,我们首先将点变换到3D cuboid坐标系,然后与cuboid尺寸进行比较,得到三维误差:
![]()
Camera-point measurement:
![]()
zm 是 3D 点 P 的像素坐标。
Data association
跨帧数据关联是slam的另一个重要部分。与特征点匹配相比,物体关联似乎更容易,因为包含了更多的纹理,可以使用许多二维物体跟踪或模板匹配方法。 在一些简单的场景中,甚至二维方框重叠也可以work。 但是,如果存在严重的物体遮挡和重复物体,这些方法就不稳健了。此外,在目前的slam优化中,需要检测并移除动态物体,但标准的物体跟踪方法无法分类是否静态,除非使用特定的运动分割方法。

作者提出了另一种基于特征点匹配的物体关联方法。对于许多基于特征点的slam方法,不同视图中的特征点可以通过描述子匹配和对极几何检查进行有效匹配。因此,我们首先将特征点与对应的物体关联起来,条件是至少有两帧图像在二维物体边界框中观察到了特征点,且特征点与立方体中心的三维距离小于 1 米。
在公式 11 中计算 BA 过程中的对象点测量误差时,也会用到这种对象点关联。
如果不同帧中的两个物体之间共享的特征点数量最多,并且超过了一定的阈值(论文中为 10 个),我们就会匹配这两个物体。属于移动物体的动态特征点会被丢弃,因为无法满足对极约束。因此,相关特征点较少的物体被视为动态物体。
四、DYNAMIC SLAM
提出了一种联合估计相机位姿和动态物体轨迹的方法。对物体做了一些假设,以减少未知参数的数量,使问题变得可解。
常用的两个假设是:物体是刚性的,并遵循某种物理上可行的运动模型。
刚体假设:一个点在其相关物体上的位置不会随时间改变。这样,我们就可以利用重投影误差来优化其位置。
运动模型:最简单的形式是匀速恒定运动模型。对于某些特定物体(如车辆),还需要遵循nonholonomic wheel model(没有侧滑)。
使用“动态点”来指代与运动物体相关的特征点。对于运动物体 Oi 上的动态点 Pk,我们用 iPk 表示其在物体上的锚定位置,该位置基于刚性假设是固定的。其世界坐标系下的位姿会随时间变化,不适合slam优化。
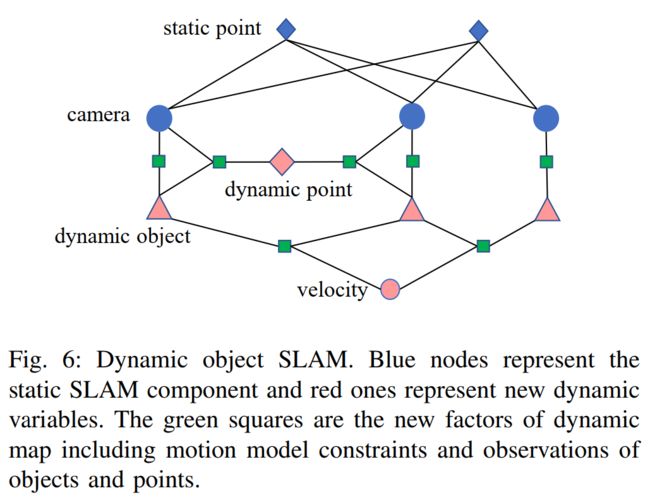
如上图所示,绿色节点代表误差中的各项约束。有了这些因子,相机的位姿也可以通过动态元素来约束。
Object motion model:物体运动可以用变换矩阵T来表示。我们可以将T应用于之前的位姿,然后计算当前位姿误差。在这里,我们采用了nonholonomic wheel model,汽车运动由速度v和转向角Φ表示,根据先验假设,其变换矩阵为:
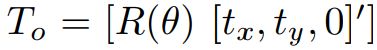
状态转移可以表示为:

其中 L 为前后车轮中心之间的距离。请注意,该模型要求 x、y、θ 定义在后轮中心,而我们的目标坐标系定义在车辆中心。这两个坐标系有 L/2 的偏移。最终的运动模型误差:
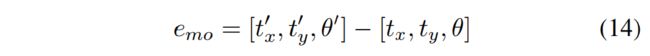
Dynamic point observation:动态点是锚定在相关物体上的,因此首先要将其转换到世界坐标系,然后再投射到相机坐标系上。假设第 k 个点在第 i 个物体上的位置为 iPk,而第 j 幅图像中的物体位姿为jToi,则该点的重投影误差为:
![]()
在数据关联方面,上节中针对静态环境的关联方法并不适用于动态情况,原因是难以匹配动态点特征。跟踪特征点的典型方法是描述子匹配,然后检查对极约束。然而,对于单目动态情况,很难准确预测物体和点的移动。
所以通过二维 KLT 稀疏光流算法直接跟踪特征点,不需要三维点位置。
假设两帧图像的投影矩阵分别为 M1、M2。这两个帧中的三维点位置分别为 P1、P2,对应的像素分别为 z1、z2。两帧之间的物体移动变换矩阵为 ∆T,那么我们可以推断出 P2 = ∆TP1。根据投影规则,我们可以得出:
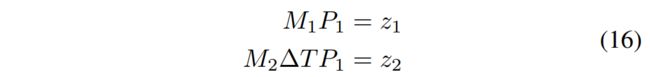
可以用 SVD 求解三角化。
当像素位移较大时,KLT 跟踪仍可能失败。因此,在动态目标跟踪中,直接使用视觉物体跟踪算法。首先跟踪物体的二维边界框,并根据上一帧预测其位置,然后将其与当前帧中重叠率最大的检测边界框进行匹配。
五、实验
2D目标检测方面,采用yolo检测室内场景,ms-cnn检测室外场景。
slam方面采用ORB SLAM2。
展望一下,使用object建立稠密图,更全面的场景理解等等。