机器学习——支持向量机（数学基础推导篇）

在一个周日下午，夏天的雨稀里哗啦地下着
我躺在床上，捧着ipad看支持向量机
睡了好几个觉…支持向量机太好睡了
拉格朗日乘数法太好睡了
几何函数太好睡了
在我看来，支持向量机是目前学下来，最难以理解的内容
希望日后不要太难…脑子不支持的

1. 支持向量机的数学困惑

支持向量积的原理，网上已经有很多人解释了。
支持向量机（SVM）——原理篇
机器学习笔记（五）：支持向量机（SVM）
支持向量机算法（SVM）详细讲解(含手推公式）
但即使看了原理篇，依然有绊倒自己的地方，或许是自己数学基础跟不上各大阿婆主，只好自己列出困惑的数学问题。

当数据集线性可分时，假设有一个线性函数能将数据集分类，这就是感知机模型该做的事：找到能让数据集线性划分的一个线性函数 $y=\sum w_i{x}_i+b$

但实际上，不一定只有一个线性函数，能线性划分数据集，那么哪个线性函数的划分效果更好呢？这就是支持向量机进一步要做的事。

支持向量机是以感知机为基础，进一步要求线性函数划分距离更宽：也就是线性函数两侧的数据集，距离最远，即求出线性函数对称两侧的最大宽度距离2d

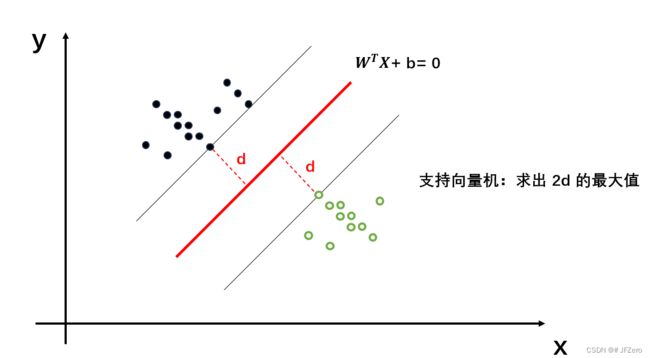
这挺好理解的，要想井水不犯河水，那就离得远远的。最好是一个天上，一个地下，互不打扰
比如深海里的鲨鱼，和高空上的雄鹰，这俩就不是一类…因为离得太远…好吧，这个比喻纯粹扯淡了
从逻辑上来说，空间距离越大，差异越大，这是公认事实。

但要怎么求出2d的最大值呢？

这就要涉及到我困惑很久的第一个问题：点到线（点到面或超平面）的距离计算公式

1.2 第一个数学困惑：点到线（面）的距离公式

$d=\frac{|W^{T}X+b|}{||W|{|}_2}$

为什么是这个公式？？这让我困惑很久…数学没学好

我试着从几何的角度，从一元线性函数、二元线性函数图像上去推导，但仅仅能推导到二元，一旦涉及到三元【三维空间】，我脑子就废了

后来，无意间看到一个博主的解释

恍然大悟，哦~~~~
但哦什么呢。。。。这个法向量n是怎么算的

如果超平面的函数为 $A{x}_1+B{x}_2+C{x}_3+D=0$
求点$x_b$到超平面 $A{x}_1+B{x}_2+C{x}_3+D=0$的距离，（设点$x_a$位于平面上）

那个博主说法向量设为 $n^{\to }=(A,B,C)$

则向量 ${x_a{x}_b}^{\to }=(x_{a1}-x_{b1},x_{a2}-x_{b2},x_{a3}-x_{b3})$

$d=\frac{{x_a{x}_b}^{\to }\ast n^{\to }}{|n^{\to }|}=\frac{A(x_{a1}-x_{b1})+B(x_{a2}-x_{b2})+C(x_{a3}-x_{b3})}{\sqrt{A^2+B^2+C^2}}$

由于点$x_a$位于平面上，因此$A{x}_{a1}+B{x}_{a2}+C{x}_{a3}+D=0$
则$A{x}_{a1}+B{x}_{a2}+C{x}_{a3}=-D$

则分子部分：$A(x_{a1}-x_{b1})+B(x_{a2}-x_{b2})+C(x_{a3}-x_{b3})$
$=-(A{x}_{b1}+B{x}_{b2}+C{x}_{b3}+D)$

整合起来的$d=\frac{|{x_a{x}_b}^{\to }\ast n^{\to }|}{|n^{\to }|}=\frac{|A(x_{a1}-x_{b1})+B(x_{a2}-x_{b2})+C(x_{a3}-x_{b3})|}{\sqrt{A^2+B^2+C^2}}=\frac{|-(A{x}_{b1}+B{x}_{b2}+C{x}_{b3}+D)|}{\sqrt{A^2+B^2+C^2}}$

这不就是 $d=\frac{|W^{T}X+b|}{||W|{|}_2}$ 的公式了嘛！！！

但要注意：$d=\frac{|W^{T}X+b|}{||W|{|}_2}$公式，表示的是点到中间分类函数线的距离

不同的点，计算出的d值是不同的。

顿悟!!
但问题又来了

凭什么法向量可以设为 $n^{\to }=(A,B,C)$

这也是困惑很久的小问题，但也可以证明：首先知道法向量是垂直于平面的

求法向量$n^{\to }=(x_{n1},x_{n2},x_{n3})$

那么当平面上有两个不共线的向量 $Q^{\to }=(x_{q1},x_{q2},x_{q3})$, $F^{\to }=(x_{f1},x_{f2},x_{f3})$

法向量与这两个向量的乘积均为0
$n^{\to }\ast Q^{=}{x}_{n1}{x}_{q1}+x_{n2}{x}_{q2}+x_{n3}{x}_{q3}=0$
$n^{\to }\ast F^{=}{x}_{n1}{x}_{f1}+x_{n2}{x}_{f2}+x_{n3}{x}_{f3}=0$
上述两个式子相减得到$x_{n1}(x_{f1}-x_{q1})+x_{n2}(x_{f1}-x_{q2})+x_{n3}(x_{f1}-x_{q3})=0$

并且由于向量$Q^{\to }和F^{\to }$都在平面上，因此:
$A{x}_{q1}+B{x}_{q2}+C{x}_{q3}+D=0$
$A{x}_{f1}+B{x}_{f2}+C{x}_{f3}+D=0$
上述两个式子相减$A(x_{f1}-x_{q1})+B(x_{f1}-x_{q2})+C(x_{f1}-x_{q3})=0$

综合可得：
$x_{n1}(x_{f1}-x_{q1})+x_{n2}(x_{f1}-x_{q2})+x_{n3}(x_{f1}-x_{q3})=0$
$A(x_{f1}-x_{q1})+B(x_{f1}-x_{q2})+C(x_{f1}-x_{q3})=0$

因此，可以设$x_{n1}=A$,$x_{n2}=B$,$x_{n3}=C$
因此法向量可以设为函数的系数！！！！

又悟了！！！数学渣渣的困惑。。。终于悟了

1.3 第二个数学困惑：距离公式的分子用1来计算

教科书，包括很多up主，在求解最大宽度距离$2d=\frac{2|W^{T}X+b|}{||W|{|}_2}$时，又转化为 求$\frac{2}{||W|{|}_2}$的最大值

why??

其实我也悟了。。。但太困了。。。明天再搞吧

公式推导一下：

将划分数据集的分类函数为$A{x}_1+B{x}_2+C{x}_3+D=0$

而两侧对称的边界函数分为设为：

• $A{x}_1+B{x}_2+C{x}_3+D=Q$，移项得$A{x}_1+B{x}_2+C{x}_3+D-Q=0$
• $A{x}_1+B{x}_2+C{x}_3+D=-Q$，移项得$A{x}_1+B{x}_2+C{x}_3+D+Q=0$

这两个函数之间的距离，并不是2Q，而是 $\frac{2Q}{||W|{|}_2}$

为什么是这样呢？

假设
点$x_a$位于$A{x}_1+B{x}_2+C{x}_3+D-Q=0$边界函数上（下边界）
点$x_b$位于$A{x}_1+B{x}_2+C{x}_3+D+Q=0$边界函数上（上边界）
$A{x}_1+B{x}_2+C{x}_3+D-Q=0$和$A{x}_1+B{x}_2+C{x}_3+D+Q=0$是以$A{x}_1+B{x}_2+C{x}_3+D=0$对称分布的平行的边界函数
设点$x_a$和点$x_b$的连线，垂直于这两条边界函数，则向量$x_a{x}_b^{\to }$则相当于这两个边界函数的法向量，同时模|$x_a{x}_b^{\to }$|表示两个边界函数的距离。

现在要求的就是模|$x_a{x}_b^{\to }$|，即两个边界函数的距离。

法向量设为 $n^{\to }=(A,B,C)$

则向量 ${x_a{x}_b}^{\to }=(x_{a1}-x_{b1},x_{a2}-x_{b2},x_{a3}-x_{b3})$

$d_{边界}=\frac{{x_a{x}_b}^{\to }\ast n^{\to }}{|n^{\to }|}=\frac{A(x_{a1}-x_{b1})+B(x_{a2}-x_{b2})+C(x_{a3}-x_{b3})}{\sqrt{A^2+B^2+C^2}}$

由于点$x_a$有$A{x}_{a1}+B{x}_{a2}+C{x}_{a3}+D-Q=0$
点$x_b$有$A{x}_{b1}+B{x}_{b2}+C{x}_{b3}+D+Q=0$
则上述两式相减可得：$A(x_{a1}-x_{b1})+B(x_{a2}-x_{b2})+C(x_{a3}-x_{b3})-2Q=0$

则$d_{边界}=\frac{|{x_a{x}_b}^{\to }\ast n^{\to }|}{|n^{\to }|}=\frac{|A(x_{a1}-x_{b1})+B(x_{a2}-x_{b2})+C(x_{a3}-x_{b3})|}{\sqrt{A^2+B^2+C^2}}=\frac{2Q}{\sqrt{A^2+B^2+C^2}}$

因此，两个边界函数的公式可对应为

• $W^{T}X+b=Q$
• $W^{T}X+b=-Q$
  且两个边界函数的距离为$\frac{2Q}{||W|{|}_2}$

而实际边界函数的W、b系数同比例增大或减小，对函数是毫无影响的

就比如2x + 4 = 0 与 x+2 = 0 本质都是相同的函数。

因此可对两个边界函数的W和b参数进行同比例的缩放

• $W^{T}X+b=Q$，变为${\frac{W}{Q}}^{T}X+\frac{b}{Q}=1$
• $W^{T}X+b=-Q$，变为${\frac{W}{Q}}^{T}X+\frac{b}{Q}=-1$

此时，系数更新为$W=\frac{W}{Q}$，$b=\frac{b}{Q}$
因此两个边界函数最终变为了

• $W^{T}X+b=1$
• $W^{T}X+b=-1$

并且两个边界函数的距离为 $d_{边界}=\frac{2}{||W|{|}_2}$

至此，证成！！！
妈呀…应该是对的吧！！！

但其实我有个困惑，最初证明的点到线（面）的距离公式，以及两个边界函数的距离公式，分别有什么意义呢？

支持向量机，到底是要求距离中间分类线最近的点到线（面）的距离最大，还是要求两个边界函数的距离最大呢？

本质上看，这两个要求其实都是同一个要求，但实际上这两个要求所进行的计算方式是不同的。

如果是要求距离中间分类线最近的点，到中间分类函数的距离最大，那就必须先能求出中间分类函数——但实际我们没有边界函数，是没办法求出中间分类函数的。

- 因此，应该是要求两个边界函数的距离最大，因为两个边界函数的最大距离，实际是可以根据“拉格朗日乘数法”求的。

听起来很绕口，但实际就是我们可以假设一个分类函数

这个分类函数有参数W，那么假设两个边界函数分别在这个分类函数的两侧

我们无需计算出具体的参数b，只要根据参数W，就可以求出两个边界函数的距离

• $d_{边界}=\frac{2}{||W|{|}_2}$
  但要注意，边界函数是要能够将数据集分类的，因此边界函数的还要满足以下两个条件
• $W^{T}X+b\ge 1$时，$y=1$，要求分类正确，即$y\ast (W^{T}X+b)\ge 1$
• $W^{T}X+b\le -1$时，$y=-1$，要求分类正确，即$y\ast (W^{T}X+b)\ge 1$
• 整合起来就是两条边界函数均满足：$y\ast (W^{T}X+b)\ge 1$

因此，我们只需求出$d_{边界}$的最大值，并且满足条件$y\ast (W^{T}X+b)\ge 1$，即可得到模型的最优解。

那么究竟要怎么在有条件限制$y\ast (W^{T}X+b)\ge 1$的情况下，求出极值$d_{边界}=\frac{2}{||W|{|}_2}$呢？
这就涉及到拉格朗日乘数法了
这痛苦的让人哭泣的拉格朗日
明天继续吧！！

• 求$d_{边界max}=\frac{2}{||W|{|}_2}$，实际相当于求 $\frac{W^2}{2}$的最小值

要是换以前，求最小值，要么用求导法或是用梯度下降法，就可以实现。
但现在不行了，因为求最小值时，是有条件约束的。

如何求条件约束下的极小值呢？

1.4 第三个数学困惑：拉格朗日乘数法的数理推导

这就要用到号称“条件极值杀手”的【拉格朗日乘数法】了。

死脑筋用拉格朗日乘数法，其实会比较简单，
但真的要理解拉格朗日乘数法，真的是头疼

首先，当要求的原函数为f(x,y)，条件约束为等式约束g(x,y)=0时，求条件约束下的原函数极小值。

• 原函数：$f(x,y)$
• 等式约束条件：$g(x,y)=0$
• 求 $min(f(x,y))$

拉格朗日乘数法的计算过程为求$L(x,y)=f(x,y)+\lambda g(x,y)$的极值

• $L_x^{\prime }=f_x^{\prime }+\lambda g_x^{\prime }$
• $L_y^{\prime }=f_x^{\prime }+\lambda g_x^{\prime }$
• $L_{\lambda }^{\prime }=g(x,y)$
• 并解出x,y,λ的值，其中 x,y就是可能的符合约束条件下的极小值

看到这的时候，我直觉是合理的，但不知道是如何得出这样的计算过程，并产生了几个问题：

• 为什么有λ？
• 为什么可以构成拉格朗日函数？
• 为什么求出拉格朗日函数极值，就可以求出符合约束条件的极小值？？？

所以自己又翻阅了很多知乎阿婆主的各种解释
终于功夫不负爱搜索的人

很多人的解释是：用等高线来绘制原函数f(x,y)时，会呈现层层嵌套的圈圈，然后绘制g(x,y)时，很多人却又不是用等高线来绘制g(x,y)，然后很多人的解析就直接说g(x,y)取到极值的时候（与f(x,y)相切），就取到了符合约束条件的最小值。

说实话，几何法我还是不太理解

从KKT条件推导穿越回来的我，不得不俯首痛哭
还是要把基础打好，先理解好导数、偏导数、微分、偏微分、全微分、梯度、方向导数这些基础概念
不然自己理解起来，会十分混淆，一知半解
是的，基础很重要

找到有个up主的数理推导：
通过g(x,y)=0，说明这个g(x,y)是隐函数，然后我们可设为显函数$y={\phi }_1(x)$

然后代入f原函数：$z=f(x,{\phi }_1(x))$，用z表示代入后的函数表达，使得z与原函数f区分开

• $z_x^{\prime }=\frac{əf}{əx}+\frac{əf}{əy}\frac{d{\phi }_1(x)}{dx}=f_x^{\prime }+f_y^{\prime }\ast {\phi }_{1x}^{\prime }$
  同样的，g(x,y)=0也可以推出$x={\phi }_2(y)$，代入f原函数：$z=f({\phi }_2(y),y)$
• $z_y^{\prime }=\frac{əf}{əy}+\frac{əf}{əx}\frac{d{\phi }_2(y)}{dy}=f_y^{\prime }+f_x^{\prime }\ast {\phi }_{2y}^{\prime }$

根据隐函数求导法则：$\frac{dy}{dx}=-\frac{F_x^{\prime }}{F_y^{\prime }}$为什么隐函数求导法则是这样的，后续再证明
则知道

• ${\phi }_{1x}^{\prime }=\frac{dy}{dx}=-\frac{g_x^{\prime }}{g_y^{\prime }}$
• ${\phi }_{2y}^{\prime }=\frac{dx}{dy}=-\frac{g_y^{\prime }}{g_x^{\prime }}$
  因此
• $z_x^{\prime }=f_x^{\prime }+f_y^{\prime }\ast {\phi }_{1x}^{\prime }=f_x^{\prime }-f_y^{\prime }\ast \frac{g_x^{\prime }}{g_y^{\prime }}=f_x^{\prime }-\frac{f_y^{\prime }}{g_y^{\prime }}\ast g_x^{\prime }$
• $z_y^{\prime }=f_y^{\prime }+f_y^{\prime }\ast {\phi }_{2y}^{\prime }=f_y^{\prime }-f_2^{\prime }\ast \frac{g_y^{\prime }}{g_2^{\prime }}=f_y^{\prime }-\frac{f_x^{\prime }}{g_x^{\prime }}\ast g_y^{\prime }$

要使z取到极值，必要条件是偏导数都为0

• $z_x^{\prime }=0，因此f_x^{\prime }-\frac{f_y^{\prime }}{g_y^{\prime }}\ast g_x^{\prime }=0，推出\frac{f_x^{\prime }}{f_y^{\prime }}=\frac{g_x^{\prime }}{g_y^{\prime }}=0$
• $z_y^{\prime }=0，因此f_y^{\prime }-\frac{f_x^{\prime }}{g_x^{\prime }}\ast g_y^{\prime }=0，推出\frac{f_y^{\prime }}{f_x^{\prime }}=\frac{g_y^{\prime }}{g_x^{\prime }}=0$

设$\lambda =-\frac{f_y^{\prime }}{g_y^{\prime }}=-\frac{f_x^{\prime }}{g_x^{\prime }}$，则有

• $z_x^{\prime }=f_x^{\prime }-\frac{f_y^{\prime }}{g_y^{\prime }}\ast g_x^{\prime }=f_x^{\prime }+\lambda \ast g_x^{\prime }$
• $z_y^{\prime }=f_y^{\prime }-\frac{f_x^{\prime }}{g_x^{\prime }}\ast g_y^{\prime }=f_y^{\prime }+\lambda \ast g_y^{\prime }=0$

融入了约束条件的函数f求得极值点，需要令x,y的偏导数均为0

那么令$\lambda =-\frac{f_y^{\prime }}{g_y^{\prime }}=-\frac{f_x^{\prime }}{g_x^{\prime }}$，函数取到极值
em。。。这式子很整齐，但这是个什么式子呢？？？？
根据隐函数的求导法则可知$\frac{f_x^{\prime }}{f_y^{\prime }}=-\frac{dy}{dx}$, $\frac{g_x^{\prime }}{g_y^{\prime }}=-\frac{dy}{dx}$
所以，$\frac{f_x^{\prime }}{f_y^{\prime }}=\frac{g_x^{\prime }}{g_y^{\prime }}$可以表示f(x,y)和g(x,y)的切线斜率相等
哇！！！这不就出来了吗！！！这不就是很多人用几何作图来表示的，为什么f(x,y)和g(x,y)在两函数的切线处取到极值吗!!!!用数学推导应该是这样证明的吧！！！！

但是，后边KKT条件推导的我穿越回到这里，还是要唾骂一声：
因为如果$f_x^{\prime }$和$f_y^{\prime }$都是0的时候，就推不出$\frac{f_y^{\prime }}{f_x^{\prime }}=\frac{g_y^{\prime }}{g_x^{\prime }}$啦！！！！！！！

总之，当函数取到极值时$\lambda =-\frac{f_y^{\prime }}{g_y^{\prime }}=-\frac{f_x^{\prime }}{g_x^{\prime }}$，可推出，得到两个方程：

• $z_x^{\prime }=f_x^{\prime }+\lambda \ast g_x^{\prime }=0$
• $z_y^{\prime }=f_y^{\prime }+\lambda \ast g_y^{\prime }=0$
  对这两个式子左右两边分别乘以dx和dy，得到：
• $z_x^{\prime }dx=f_x^{\prime }dx+\lambda \ast g_x^{\prime }dx=\frac{əf}{əx}dx+\lambda \ast \frac{əg}{əx}dx=0$
• $z_y^{\prime }dy=f_y^{\prime }dy+\lambda \ast g_y^{\prime }dy=\frac{əf}{əy}dy+\lambda \ast \frac{əg}{əy}dy=0$
  对上述两个式子左右两边相加，得到：
• $z_x^{\prime }dx+z_y^{\prime }dy=\frac{əf}{əx}dx+\frac{əf}{əy}dy+\lambda \ast \frac{əg}{əx}dx+\lambda \ast \frac{əg}{əy}dy=0$
  对上述式子左右两边进行积分
• $z(x,y)=f(x,y)+\lambda g(x,y)$

而这个z函数，正是我们最后的拉格朗日函数$L(x,y,\lambda )=f(x,y)+\lambda g(x,y)$

将g(x,y)=0约束条件融入原函数f(x,y)后，成为了拉格朗日函数$L(x,y,\lambda )=f(x,y)+\lambda g(x,y)$

• 于是，原本有约束条件的f(x,y)求极值问题，变为了无约束条件的拉格朗日函数$L(x,y,\lambda )=f(x,y)+\lambda g(x,y)$求极值问题

并且当$\lambda =-\frac{f_y^{\prime }}{g_y^{\prime }}=-\frac{f_x^{\prime }}{g_x^{\prime }}$时，即原函数f(x,y)与约束条件g(x,y)函数相切时，下列式子成立，即可根据下列式子，求出x,y,λ后，求出拉格朗日函数的极值，即原目标函数f(x,y)在约束条件下的极值

• $L_x^{\prime }=f_x^{\prime }+\lambda \ast g_x^{\prime }=0$
• $L_y^{\prime }=f_y^{\prime }+\lambda \ast g_y^{\prime }=0$
• $L_{\lambda }^{\prime }=g(x,y)=0$

拉格朗日乘数法的求极值，可以转化为$(f_x^{\prime }，f_y^{\prime })+\lambda (g_x^{\prime }，g_y^{\prime })=\Delta f+\lambda \Delta g=0$

• 这不就是原函数f(x,y)的梯度与约束条件g(x,y)的梯度共线的意思吗！！！！
• 这个非常重要，尤其在后边KKT问题的理解上，显得尤为重要。

我天呐！！！！我感觉完成了一大壮举！！！虽然我觉得偏导数、导数符号可能稍微有点儿问题
但没关系啊。。。至少，在我目前的认知层面来说。。。能圆过去

主要参照了两篇文章，并结合理解（其实这两篇文章中间都有我不理解的地方，但这么一相互融合理解，忽然就懂了呀！）
拉格朗日乘数法推导
拉格朗日乘数法理解

但问题尚未结束，因为之前引用了隐函数求导法则，但还不知道隐函数求导法则究竟是怎么推导出来的

1.4 第四个数学困惑：隐函数求导法则的公式推导

这是很简单的，看别人的就好

隐函数求导法则的证明——某博主

1.5 第五个数学困惑：不等式约束条件为什么可以用拉格朗日乘数法

这是我理解到一半，就头晕地想放弃的
好难理解，如果要更透彻的了解【透彻！！！】，需要铺垫的知识：

• 梯度与偏导数的关系
• 偏导数与全微分的关系
• 梯度总是指向函数增长最大的方向
  • 涉及了偏导数与切平面的理解
  • 涉及了切线与切平面的理解

首先，拉格朗日乘数法是在约束条件为等式的情况下推导出来的。

但支持向量机要解决的是：

• $求min：\frac{w^2}{2}$，约束条件是：$y_i(w_i{x}_i+b)\ge 1$
  但拉格朗日乘数法要求的约束条件是等式约束，但支持向量机却是非等式约束

那这种情况下，就需要对进一步地讲解拉格朗日乘数法为什么可以用在不等式条件约束下。

假设原函数是f(x,y)，约束条件为不等式g(x,y)≤0

那么，可以引入松弛变量α²，使得g(x,y)+α²=0，这样就可以应用拉格朗日乘数法，将约束条件融入原函数中，求得极值，即
$L(x,y,\lambda ,\alpha )=f(x,y)+\lambda g(x,y)+\lambda {\alpha }^2$，对L函数中的未知数、系数分别求偏导，并使偏导分别为0，即可求出极值

• $L_x^{\prime }=f_x^{\prime }+\lambda g_x^{\prime }=0$ - - - - -①
• $L_y^{\prime }=f_y^{\prime }+\lambda g_y^{\prime }=0$ - - - - -②
• $L_{\lambda }^{\prime }=g(x,y)+{\alpha }^2=0$ - - - - -③
• $L_{\alpha }^{\prime }=2\lambda \alpha =0$ - - - - -④
  对于①中$2\lambda \alpha =0$，有两种情况：λ=0或α=0
  • 当λ=0时，相当于α²≠0，由③g(x,y)+α²=0可推出g(x,y)＜0【当然α²还是又可能＝0的，但无所谓】
    • 此时，$L(x,y,\lambda ,\alpha )=f(x,y)$，说明λ=0时，g(x,y)≤0对原函数f(x,y)并无约束作用
  • 当α=0时，λ要＞0【这个是需要另外证明】，则g(x,y)+α²=0可推出g(x,y)=0【当然α²还是又可能＝0的，但无所谓】
  • 因此可总结得到
    • 当g(x,y)<0时，必须使λ=0
    • 当g(x,y)=0时，λ≥0
  • α对于求原函数极值无任何影响，因此，为了更简便的计算，则可将原拉格朗日函数转化为以下无α的不等式条件约束下的拉格朗日函数
  • $L(x,y,\lambda )=f(x,y)+\lambda g(x,y)$
    • $L_x^{\prime }=f_x^{\prime }+\lambda g_x^{\prime }=0$ - - - - -①
    • $L_y^{\prime }=f_y^{\prime }+\lambda g_y^{\prime }=0$ - - - - -②
    • $L_{\lambda }^{\prime }=g(x,y)=0$ - - - - -③
    • g(x,y)≤0 - - - - -④
    • λ≥0 - - - - -⑤
      约束条件是非等式约束时，通过引入α²松弛变量，我们可以将它化为等式约束，再进一步应用拉格朗日乘数法，并通过求偏导后发现，α对约束条件和原函数的影响，可以转化为λ与原函数的关系，因此去掉松弛变量，以简约的方式呈现拉格朗日乘数法
  • 当λ＞0时，极值还是在相切的地方，即Δf + λΔg = 0 处取得
  • 当λ=0 时，极值点不在相切处，但满足条件g(x,y)<0

1.6 第六个数学困惑：不等式约束的拉格朗日乘子为什么要λ≥0

这就要用到之前推导拉格朗日乘数法时，得到的推导结果：
拉格朗日乘数法的求极值，可以转化为$(f_x^{\prime }，f_y^{\prime })+\lambda (g_x^{\prime }，g_y^{\prime })=\Delta f+\lambda \Delta g=0$

• 这不就是原函数f(x,y)的梯度与约束条件g(x,y)的梯度共线的意思吗！！！！

并且要知道，梯度的方向，指向函数值增长最大的方向【为什么？这个后续证明】

实在懒得在电脑画图了，但其实我还是有点儿小困惑的，λ<0，会妨碍到原函数在切线处取到极值
如果$f(w)=\frac{w^2}{2}$，在g(w,b)≤0的可行域内，f(w)的梯度，极有可能与g(w,b)共线同向
那么当λ<0时，$\Delta f+\lambda \Delta g$，就可以等于0，这意味着拉格朗日函数取到极值
但实际，此时在可行域内取到的拉格朗日极值，并非等同于原函数取到极值
因为在可行域内，原函数f(w)值是$\frac{w^2}{2}＞0$，实际原函数的极值点，应该在可行域圈上取得。
即，λ<0，会使得函数在Δf≠0处取到拉格朗日极值
因此λ不应小于0，而是λ≥0【至于论证λ大于0就可以的活，还是留给别人吧，算了还是自己分析吧】

• 因为λ>0时，当f的极值点在可行域圈上时，Δf和Δg同向，那么Δf+λΔg≠0，因此，λ＞0可以避免在可行域内取到拉格朗日极值点
  

1.7 第七个数学困惑：为什么梯度指向函数增长最大的方向

首先，梯度是各个方向的偏导数形成的向量

• 如果是一元函数，则导数是函数值对单个变量的一条切线
• 如果是二元函数，则函数值对两个变量的偏导数，梯度为$(f_x^{\prime },f_y^{\prime })$，这两个偏导数表示的切线即为两条切线且这两条切线不共线，这两条不共线的切线构成了一个切平面，
  如果是…

以二元函数为例，讲解为什么梯度指向函数增长最大的方向

首先，梯度是由各个偏导数形成的向量，函数的增长量为$dz=f_x^{\prime }dx+f_y^{\prime }dy$

如果x偏导数$f_x^{\prime }=\frac{\Delta z}{\Delta x}>0$，意味着当固定y不变，沿着x正方向移动时，z是增长最大的
如果x偏导数$f_x^{\prime }=\frac{\Delta z}{\Delta x}＜0$，意味着当固定y不变，沿着x负方向移动时，z是增长最大的

• 由此可见，偏导数为正或为负，均指向了函数值增长最大的方向
• 对于y的偏导数分析亦是如此

那么，偏导数均指向了函数值增长最大的方向，即由偏导数构成的梯度向量，即指向函数值增长最大的方向$\Delta z=(f_x^{\prime },f_y^{\prime })$

那么在函数值等高线中，梯度方向则是由内指向外侧的向量

非等式约束：$y_i(w_i{x}_i+b)\ge 1$，要转化为与求解的极值同向：

• 即求min时，非等式约束需要转化为$1-y_i(w_i{x}_i+b)\le 0$求min时，约束必须是≤0
• 求max时，非等式约束需要转化为$y_i(w_i{x}_i+b)-1\ge 0$求max时，约束必须是≤0
  why????说实话，我到现在都不理解为什么一定要同向，为什么为什么为什么？？？后续再慢慢想吧，反正不耽误后续的推导

2.支持向量机的数学推导

2.1 拉格朗日乘数法——KKT条件

考虑到支持向量机求得是$求原函数minf(w)：\sum \frac{w_i^2}{2}$，则约束条件应该为
$g_i(w,b)=(1-y_i(W{X}_i+b))\le 0$
匹配上对应的拉格朗日乘子${\lambda }_i$，即为${\lambda }_i{g}_i(w,b)={\lambda }_i(W{X}_i+b)\le 0$

注意：这里的$i$ 表示一个对象，该对象的特征元素为$X_i$，分类结果为 $y_i$，$g_i(w,b)$表示该对象要满足的约束条件，${\lambda }_i$表示该对象的拉格朗日乘子

那么，如果有n个对象（即n条数据），那么就有n个约束条件${\sum }_1^n{\lambda }_i{g}_i(w,b)$

支持向量机中已知数据是x,y，而参数w,b未知，因此是通过拉格朗日乘数法求取w和b

• 求目标函数极小值$min:f(w)=\sum \frac{w^2}{2}$ , 约束条件为：${\sum }_1^n{g}_i(w,b)$
  构建拉格朗日函数：$L(w,b,\lambda )=\sum \frac{w^2}{2}+{\sum }_1^n{\lambda }_i{g}_i(w,b)$
  • $L_w^{\prime }=f_w^{\prime }+\lambda g_w^{\prime }=W-\sum {\lambda }_i{y}_i{X}_i=0$
  • $L_b^{\prime }=f_b^{\prime }=\lambda g_b^{\prime }=-\sum {\lambda }_i{y}_{i}b=0$
  • $L_{\lambda }^{\prime }=\sum g_i(w,b)=\sum (1-y_i(W{X}_i+b))=0$
  • $g(w,b)\le 0$
  • $\lambda \ge 0$

以上这些条件，实际就是KKT条件，我们要在满足以上条件的情况下，求拉格朗日函数的极值点
但以上含有多个参数 W,b,${\lambda }_i$，通过求导求解仍然十分困难
因此需要寻求新的出路
这个新出路就是拉格朗日对偶问题

2.2 拉格朗日对偶问题求解

原本通过将约束条件融入目标函数f(w)，来求$min:f(w)$，等价于
$求min:L(w,b,\lambda )=f(w)+\sum {\lambda }_i{g}_i(w,b)$

由于${\lambda }_i{g}_i(w,b)\le 0，则\sum {\lambda }_i{g}_i(w,b)\le 0，因此minL(w,b,\lambda )\le minf(w)$

• 先调整$\lambda i$，使拉格朗日函数逼近原目标函数
  • 在逼近过程中，只有当拉格朗日函数值达到最大时，才有$L(w,b,{\lambda }^{\ast })=f(w)$
  • 因此可简写调整过程为$ma{x}_{({\lambda }^{\ast })}L(w,b,\lambda )$，表示调整λ，以取到λ调整过程中L的最大值
• 再调整参数w,b，使拉格朗日函数值取到最小值min
  • 因此调整过程可写为$MI{N}_{(w,b)}MA{X}_{({\lambda }^{\ast })}L(w\ast ,b\ast ,\lambda \ast )=minf(w\ast )$

但是依然无法求解，因为先调整$\lambda$取极大值的过程，如果对λ求导，得到的g(w,b)仍然含有未知数w,b，无法判断什么时候取到极大值。

于是想办法让w,b的调整也通过 $\lambda$ 的调整来实现，就用拉格朗日的对偶问题。

也就是先调整w,b，求拉格朗日min值，再调整λ，求拉格朗日max值。
求解对偶问题：$MA{X}_{(\lambda )}MI{N}_{(w,b)}L(w,b,\lambda )$

推导一下：
由于调整w,b时，并不调整约束条件，即$\sum {\lambda }_i{g}_i(w,b)\le 0$，
因此$MI{N}_{(w,b)}L(w,b,\lambda )\le MI{N}_{(w,b\in 约束条件)}L(w,b,\lambda )$
因此
$MA{X}_{(\lambda )}MI{N}_{(w,b)}L(w,b,\lambda )\le MA{X}_{(\lambda )}MI{N}_{(w,b\in 约束)}L(w,b,\lambda )\le MA{X}_{(\lambda )}MINf(w)$

$MA{X}_{(\lambda )}MINf(w)$中，调整λ并不影响f(w)的极值，因此$MA{X}_{(\lambda )}MINf(w)=MINf(w)$

因此，$MA{X}_{(\lambda )}MI{N}_{(w,b)}L(w,b,\lambda )\le MA{X}_{(\lambda )}MI{N}_{(w,b\in 约束)}L(w,b,\lambda )\le MINf(w)$

所以，$MA{X}_{(\lambda )}MI{N}_{(w,b)}L(w,b,\lambda )$是$MINf(w)$的一个下界

要使得≤变为＝，表示为强对偶性，就需要涉及到凸优化问题【坦诚表示，懒得去理解】
“强对偶性”成立，由对偶问题的最优值即可得到主问题的最优值，强对偶成立必须满足以下条件：

• 主问题是凸优化问题： 原目标函数、不等式约束条件为凸函数；等式约束为仿射函数
• 可行域中至少有一点使不等式约束严格成立。

仿射函数即由 1 阶多项式构成的函数，一般形式为 f(x)=Ax+b，这里，A 是一个 m×k 矩阵，x 是一个 k 向量，b是一个 m 向量，实际上反映了一种从 k 维到 m 维的空间映射关系。

在支持向量机中，$f(w)=\frac{w^2}{2}$这就是个凸函数，
g(w,b)≤0，可以通过添加松弛变量α²，使得g(w,b)+α²=0，变为仿射函数，在应用拉格朗日乘数法时，简化省去了松弛变量 α²，最终g(w,b)也可视为凸函数

因此，目标函数f(w),约束条件g(w,b)≤0都是凸函数，因此拉格朗日函数L(w,b,λ)呈强对偶性

最终对偶问题的最优解，即为原问题最优解

也就是$MA{X}_{(\lambda )}MI{N}_{(w,b)}L(w,b,\lambda )=MI{N}_{(w,b)}MA{X}_{({\lambda }^{\ast })}L(w\ast ,b\ast ,\lambda \ast )=MINf(w)$

现在求解$MA{X}_{(\lambda )}MI{N}_{(w,b)}L(w,b,\lambda )=MA{X}_{(\lambda )}MI{N}_{(w,b)}\sum \frac{w^2}{2}+{\sum }_1^n{\lambda }_i{g}_i(w,b)$

• 求解$MI{N}_{(w,b)}\sum \frac{w^2}{2}+{\sum }_1^n{\lambda }_i{g}_i(w,b)$
• 先求解w,b的偏导数，并等于0
  • $L_w^{\prime }=f_w^{\prime }+\lambda g_w^{\prime }=W-\sum {\lambda }_i{y}_i{X}_i=0$
  • $L_b^{\prime }=f_b^{\prime }=\lambda g_b^{\prime }=-\sum {\lambda }_i{y}_{i}b=0$
  • 得到$W=\sum {\lambda }_i{y}_i{X}_i$
  • 得到$-\sum {\lambda }_i{y}_{i}b=0$
  • 代入可得$L(w,b,\lambda )=\sum {\lambda }_i-\frac{(\sum {\lambda }_i{x}_i{y}_i{)}^2}{2}=\sum {\lambda }_i-\frac{{\sum }_{i=1}^n{\sum }_{j=1}^n{\lambda }_i{\lambda }_j{x}_i{x}_j{y}_i{y}_j}{2}$
    
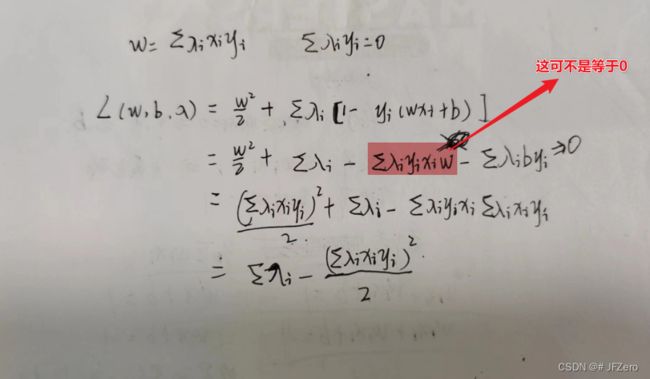
    对偶问题

最后w,b都没了，只有λ，只需求出$MA{X}_{\lambda }L(\lambda )=\sum {\lambda }_i-\frac{{\sum }_{i=1}^n{\sum }_{j=1}^n{\lambda }_i{\lambda }_j{x}_i{x}_j{y}_i{y}_j}{2}$

转化为二次凸优化问题，但考虑到如果数据量太大，那么计算起来会非常困难
因此转为用SMO算法

3. 待解决的困惑——凸优化问题

3.1 为什么凸优化可推导强对偶性

3.2 为什么仿射函数可推导出凸函数