巅峰极客2022初赛 部分题解
文章目录
-
- Crypto
-
- point-power
- strange curve
- Misc
-
- easy_Forensic
- Lost
巅峰极客2022初赛,团队共解决7道题,合计2234分,排名第11位,晋级复赛。
(Misc有一道题赛后两分钟出了o(╥﹏╥)o,交了就第二了
Crypto
point-power
给了一条椭圆曲线,参数p和b已知但是a未知,告知a即为flag。给了点G和二倍点2G的横坐标 x 1 x_1 x1、 x 2 x_2 x2。
简要推导一下可知:
λ 2 ≡ x 2 + 2 x 1 ( m o d p ) y 1 ≡ 3 x 1 2 + a 2 λ ( m o d p ) y 1 2 ≡ x 1 3 + a x 1 + b ( m o d p ) \lambda^2 \equiv x_2+2x_1 \space (mod \space p) \\ y_1 \equiv \frac{3x_1^2+a}{2\lambda}\space(mod \space p) \\ y_1^2 \equiv x_1^3+ax_1+b\space(mod \space p) λ2≡x2+2x1 (mod p)y1≡2λ3x12+a (mod p)y12≡x13+ax1+b (mod p)
因此可以用Cipolla爆破出 λ \lambda λ,再用 λ \lambda λ表示 y 1 y_1 y1后代入曲线方程。此时形成的二次多项式同余方程只有一个未知数 a a a,配方再用一次Cipolla爆破即可得到 a a a。
def eulerCriterion(a, p):
return -1 if pow(a, int((p-1)/2), p) == p-1 else 1
def cipollaMult(x1, y1, x2, y2, u, p):
return ((x1*x2 + y1*y2*u) % p), ((x1*y2 + x2*y1) % p)
def cipollaAlgorithm(n, p):
a = Mod(n, p)
out = []
if eulerCriterion(a, p) == -1:
print(str(a) + " is not a quadratic residue modulo " + str(p))
return False
if not is_prime(p):
conglst = [] #congruence list
crtlst = []
factors = []
for k in list(factor(p)):
factors.append(int(k[0]))
for f in factors:
conglst.append(cipollaAlgorithm(a, f))
for i in Permutations([0, 1] * len(factors), len(factors)).list():
for j in range(len(factors)):
crtlst.append(int(conglst[ j ][ i[j] ]))
out.append(crt(crtlst, factors))
crtlst = []
return sorted(out)
if pow(p, 1, 4) == 3:
temp = pow(a, int((p+1)/4), p)
return [temp, p - temp]
t = randrange(2, p)
u = pow(t**2 - a, 1, p)
while (eulerCriterion(u, p) == 1):
t = randrange(2, p)
u = pow(t**2 - a, 1, p)
x0, y0 = t, 1
x, y = t, 1
for i in range(int((p + 1) / 2) - 1):
x, y = cipollaMult(x, y, x0, y0, u, p)
out.extend([x, p - x])
return sorted(out)
p = 3660057339895840489386133099442699911046732928957592389841707990239494988668972633881890332850396642253648817739844121432749159024098337289268574006090698602263783482687565322890623
b = 1515231655397326550194746635613443276271228200149130229724363232017068662367771757907474495021697632810542820366098372870766155947779533427141016826904160784021630942035315049381147
x1 = 2157670468952062330453195482606118809236127827872293893648601570707609637499023981195730090033076249237356704253400517059411180554022652893726903447990650895219926989469443306189740
x2 = 1991876990606943816638852425122739062927245775025232944491452039354255349384430261036766896859410449488871048192397922549895939187691682643754284061389348874990018070631239671589727
lamSqr = (x2 + 2 * x1) % p
# lam = cipollaAlgorithm(lamSqr, p)
lam1 = 2014880882082318301445894374501675195919976436255804247056910036068932318853083532875711742303096608453631262469539522882159038073258190729304974713113937514650838613626987477596673
lam2 = 1645176457813522187940238724941024715126756492701788142784797954170562669815889101006178590547300033800017555270304598550590120950840146559963599292976761087612944869060577845293950
res = (4 * lam1 ** 2 * (x1 ** 3 + b) - 12 * x1 ** 3 * lam1 ** 2 + 4 * lam1 ** 4 * x1 ** 2) % p
# aplus = cipollaAlgorithm(res, p)
aplus1 = 1370590950134392447563290310467074091332453364778953225609598164724491850785837752848492322413374912469146392849123620624141856740898793235764218415859608726708932969579886037927449
aplus2 = 2289466389761448041822842788975625819714279564178639164232109825515003137883134881033398010437021729784502424890720500808607302283199544053504355590231089875554850513107679284963174
plus = (3 * x1 ** 2 - 2 * lam1 ** 2 * x1) % p
a1 = (aplus1 - plus) % p
a2 = (aplus2 - plus) % p
print(a1) ---> 这个是flag:56006392793430010663016642098239513811260175999551893260401436587175373756825079518464264729364083325
print(a2)
strange curve
史诗级非预期,被打烂了。
整个加密过程中只对x进行了加一操作,最后还在P坐标里给出了x的值。代入进去爆破一下发现x就是flag。(乐)
while True:
try:
y=lift(x,a,b,p)
break
except:
x+=1
continue
assert a*x*(y**2-1)%p==b*y*(x**2-1)%p
P=(x,y)
P = (56006392793427940134514899557008545913996191831278248640996846111183757392968770895731003245209281149, 5533217632352976155681815016236825302418119286774481415122941272968513081846849158651480192550482691343283818244963282636939305751909505213138032238524899)
Misc
easy_Forensic
volatility扫一下raw文件发现在cmdscan里发现使用了Explorer.exe。查一下iehistory发现桌面上存在一个111.raw文件。filescan查看一下文件,在桌面Desk上找到hint.txt,secret.zip,gift.jpg,wechat.txt等文件,尝试提取。
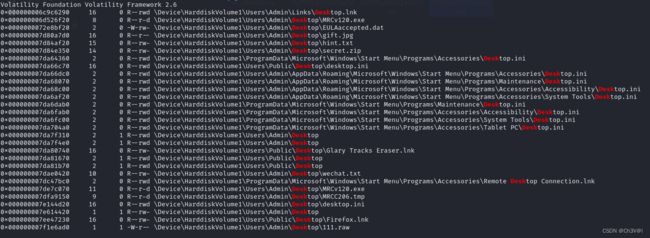
发现除了hint.txt都可以提取出来。jpg图片下方存在黑色像素点,猜测高度被修改了。增加jpg图片高度发现Passwd:Nothing is more important than your life!

尝试用password解zip失败,猜测需要提取hint.txt。Diskgenius挂载提取文件,得到提示:is_ not 。
将password中的空格改为下划线即可解压zip,拿到密钥。
A gift for You: wHeMscYvTluyRvjf5d7AEX5K4VlZeU2IiGpKLFzek1Q=
wechat.txt打开之后不可读,应该是被加密了。根据题目信息搜集查一下微信解密相关内容,尝试了多个脚本最后找到文章:https://tttang.com/archive/1665/#toc_0x04,微信数据库加密。
github查到脚本,WeChatUserDB解密拿到数据库文件,sqlite3查询得到flag。
Lost
赛后两分钟才搞出来的Misc题。
纯纯的脑洞题,但是这个脑洞确实常见,只能说时间分配很重要。(去帮着搜密码学第三题的论文耽误了时间)
给了30个zip压缩包文件,但都损坏了,里面有一个含有假flag的txt和一张图片。查看一下hex发现压缩包文件第一个PK的扩展区存在问题,但是这部分肯定无法硬爆。做提前一个小时一直在硬爆,思路偏了。
后来发现三十个压缩包几乎完全一样(这也说明肯定不是硬爆出来的),hash一下发现散列值不同,猜测压缩包之间可能存在极其细微的差别来隐藏信息。
(实际上这是国外CTF的常见隐写考法,几周前TFCCTF考过一个爆破crc32隐写的,也是给了一堆损坏的压缩包
用HexEditor比对一下发现所有文件只在第71、72两个字节存在不同,因此提取这两个字节的数据。最开始尝试的是字节i和字节i+1异或,但是得到的flag是残缺的,最后发现取相邻元素差值是flag。
k = []
for i in range(1,31):
f = open("flag{}.zip".format(i), "rb")
ss = ""
c = f.read(72)
k.append(256 * c[-2] + c[-1])
print(k)
for i in range(29):
print(chr(abs(k[i]-k[i+1])),end='')